ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Harivans Pratap Singh1, Shweta Verma2, Shailendra Mishra3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
There are many security algorithms that are used for security purpose. IDEA is one of them. The block cipher IDEA operates with 64-bit plaintext and cipher text blocks and is controlled by a 128-bit key. The fundamental innovation in the design of this algorithm is the use of operations from three different algebraic groups. The algorithm structure has been chosen such that, with the exception that different key sub-blocks are used, the encryption process is identical to the decryption process. The drawback of IDEA is that the large numbers of weak keys were found in IDEA (International Data Encryption Algorithm). Also a new attack on round 6 of IDEA has been detected. In this paper we are describe the design and implementation of secure data encryption algorithm(S-IDEA) protocol, the size of the key has been increased from 128 bits to 256 bits. This increased key size will increase the complexity of the algorithm. To increase the amount of diffusion two MA blocks (multiplicative additive block) are used in a single round of IDEA as compared to one MA block used previously in a single round, With these modifications in the proposed algorithm will increase the cryptographic strength.
Keywords |
| International data encryption algorithm(IDEA) ,Secure data encryption algorithm(S-IDEA).Multiple additive(MA) |
INTRODUCTION |
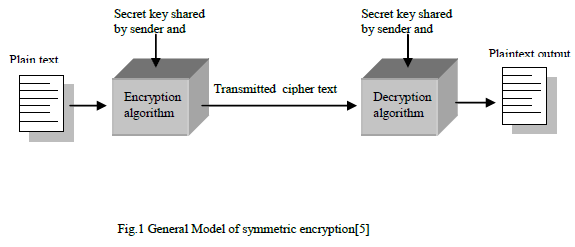
| Symmetric encryption, also referred to as conventional encryption or single key encryption was the only type of encryption in use prior to the development of public-key encryption in 1970s.It remains by far the most widely used of the two types of the encryption[5]. |
| A symmetric encryption scheme has five ingredients: |
| ïÃâ÷ Plaintext: This is the original intelligible message or data that is fed into the algorithm as input. |
| ïÃâ÷ Encryption algorithm: It performs various substitutions and transformations on the plaintext. |
| ïÃâ÷ Secret key: It is also an input to algorithm which is shared between the sender and receiver and kept secret between them. The exact substitutions and transformations performed by the algorithm depend on the key. |
| ïÃâ÷ Ciphertext: This is scrambled message produced as output. It depends on the plaintext and the secret key. The ciphertext is random stream of data and is unintelligible. |
| ïÃâ÷ Decryption algorithm: It is encryption algorithm run in reverse. It takes the ciphertext and secret key and produces the original plaintext. |
 |
DEFINITION 1. |
| A cryptosystem is a five -tuple (P, C, K, E, D), where the following conditions are satisfied: |
| 1. P is a finite set of possible plain texts. |
| 2. C is a finite set of possible ciphertexts. |
| 3. K, the keyspace, is a finite set of possible keys. |
| 4. For each K ε k, there is an encryption rule eK ε E. and a corresponding decryption rule dK ε D. Each eK : P →C and dK : C → P are functions such that dK(eK(x)) = x for every plaintext x ε P. |
| The main property is property 4. It says that if a plaintext x is encrypted using eK, and the resulting cipher text is subsequently decrypted using dK, then the original plaintext x results. |
| Cryptography may be divide in two main categorries |
| • Asymmetric: For Encryption and Decryption using a pair of keys. |
| • Symmetric: For Encryption and Decryption using the same key (or without key – in the case of Hash function) |
| All classical cryptosystems (that is cryptosystems that were developed before 1970s) are examples of symmetric keycryptosystems[6]. In addition, most modern cryptosystems are symmetric as well. Some of the most popular examples of modern symmetric key cryptosystems include AES (Advanced Encryption Standard), DES (Data Encryption Standard), IDEA, FEAL, RC5, and many others[2]. All symmetric key cryptosystems have a common property: they rely on a shared secret between communicating parties. This secret is used both as an encryption key and as a decryption key (thus the keyword "symmetric" in the name). This type of cryptography ensures only confidentiality and fails to provide the other objectives of cryptography. Even more importantly the disadvantage of symmetric key cryptography is that it cannot handle large communication networks[2]. If a node in a communication network of n nodes needs to communicate confidentially with all other nodes in the network, it needs n - 1 shared secrets. For large value of n this is highly impractical and inconvenient. On the other hand, an advantage over public key cryptosystems is that symmetric cryptosystems require much smaller key sizes for the same level of security[1]. Hence, the computations are much faster and the memory requirements are smaller (Whitfield et al, 1976) |
| In public key cryptosystems there are two different keys: a public key, which is publicly known, and the secret key, which is kept secret by the owner. The system is called “asymmetric” since the different keys are used for encryption and decryption– the public key and the private key[1]. If data is encrypted with a public key, it can only be decrypted using the corresponding private key, and vice versa[3]. Today, all public key cryptosystems rely on some computationally intractable problems. For example, the cryptosystem RSA relies on the difficulty of factoring large integers, while El-Gamal cryptosystem relies on the discrete logarithm problem (DLP), which is the problem of finding a logarithm of a group element with generator base in a finite Abelian group Public key cryptosystems do not need to have a shared secret between communicating parties. This solves the problem of large confidential communication network introduced earlier. In addition, public key cryptography opened door for ways of implementing technologies to ensure all goals of cryptography. By means of combining public key cryptography, public key certification, and secure hash functions, there are protocols that enable digital signatures, authentication, and data integrity[1]. Due to the increase in processor speed and even more due to smart modern cryptanalysis, the key size for public key cryptography grew very large. This created a disadvantage in comparison to symmetric key cryptosystems: public key cryptography is significantly slower[2], and requires large memory capacity and large computational power. As an example, a 128-bit key used with DES cryptosystem has approximately the same level of security as the 1024-bit key used with RSA public key cryptosystem (Oorschot P.C. van, et al, 1997). |
BACKGROUND AND RELATED WORK |
| The cryptographic schemes are divided into two parts. |
| 1. Classical Cryptography |
| 2. Modern Cryptography |
| Classical ciphers are often divided into transposition ciphers and ciphers. A substitution cipher replaces the one symbol with another. if the symbol in the plain text are alphabetic character ,we replace one character with another. For example assume the statement to be encrypted is “this is the final chapter”[7].We apply substitution cipher and change each character by its next ASCII character, the resultant statement would be,“uijt jt uif gjomb……….”This method is popularly known as Caesar cipher, as it was invited by Roman general Julius Carsar.Whan a character is substituted by another character, it is also known as monoalphabatic cipher. transposition cipher changes the position of character. As appose of the substitution cipher, the transposition cipher change the order but not changes the character themselves. for example reshuffle the original string by sending the first character to 2nd position ,third character to 4th position ,the fifth character to 3rd position and so on[7]. |
| Modern Cryptography |
| Public key cryptography(asymmetric) |
| (a) Encryption |
| (i) Integer factorization: RSA and Rabin encryption. |
| (ii) Discrete Logarithm: ElGamal Encryption. |
| (iii) Elliptic Curve: Elliptic Curve Cryptosystem. |
| (iv) Chaotic: Fractal Encryption. |
| (v) Others: NTRU, Gang-Harn. |
| (b) Key Sharing |
| (i) Discrete Logarithm: Diffie-Hellman. |
| (ii) Elliptic Curve: ECDH. |
| (iii) Chaotic: Fractal Key Exchange. |
| (c) Digital Signature |
| (i) Integer factorization: RSA digital signature. |
| (ii) Discrete Logarithm: DSA. |
| (iii) Elliptic Curve: ECDSA. |
| (iv) Chaotic: Fractal Digital signature. |
| Non public key |
| (a) Secret key (Symmetric) |
| (i) Block cipher: DES |
| (ii) Stream cipher. |
| (b) Hash function Secure Hash Algorithm (SHA). |
| The block cipher IDEA operates with 64-bit plaintext and cipher text blocks and is controlled by a 128-bit key. The fundamental innovation in the design of this algorithm is the use of operations from three different algebraic groups. The algorithm structure has been chosen such that, with the exception that different key sub-blocks are used, the encryption process is identical to the decryption process. The drawback of IDEA is that the large numbers of weak keys were found in IDEA (International Data Encryption Algorithm)[4]. Also a new attack on round 6 of IDEA has been detected. For this reason we have proposed secure data encryption algorithm(S-IDEA) protocol |
SYSTEM DESIGN AND IMPLEMENTATION |
Encryption for S-IDEA |
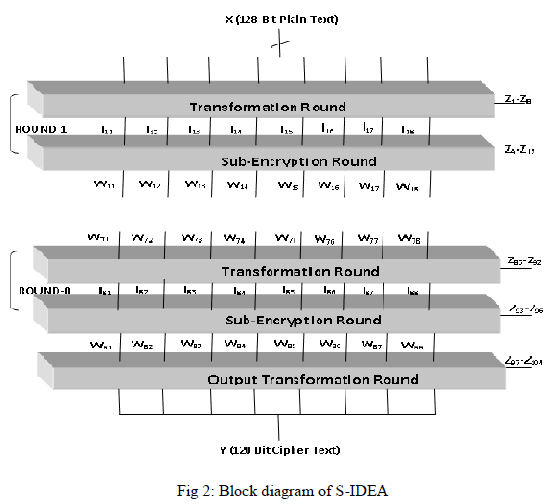
| The encryption process consists of eight identical encryption steps (known as encryption rounds) followed by an output transformation. The structure of the first round is shown in detail. |
| In the first encryption round, the first four 16-bit key sub-blocks are combined with two of the 16-bit plaintext blocks using addition modulo 216, and with the other two plaintext blocks using multiplication modulo 216 + 1. The results are then processed further as shown in Figure3.4, whereby two more 16-bit key sub-blocks enter the calculation and the third algebraic group operator, the bit-by-bit exclusive OR, is used. At the end of the first encryption round four 16-bit values are produced which are used as input to the second encryption round in a partially changed order. The process described above for round one is repeated in each of the subsequent 7 encryption rounds using different 16-bit key subblocks for each combination. During the subsequent output transformation, the four 16-bit values produced at the end of the 8th encryption round are combined with the last four of the 104 key sub-blocks using addition modulo 216 and multiplication modulo 216 + 1 to form the resulting four 16-bit cipher text blocks. |
 |
 |
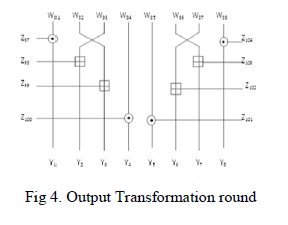
Detail of single round |
| (1)The 128 bits text is processed in 8 block of 16 bit each. |
| (2)The proposed modified version of IDEA(S-IDEA) can be seen as two sub-block of 64 bits running in parallel with each other. Each round in encryption uses two MA block and 12 keys. |
| (3)Each round consists of two further divisions i.e. Transformation followed by Sub-Encryption, transformation in each round uses 8 keys whereas sub-encryption uses 4 keys. |
| (4)The former description of keys is valid for round from 1 to 8 where as the 9th round called the Output transformation round uses 8 keys |
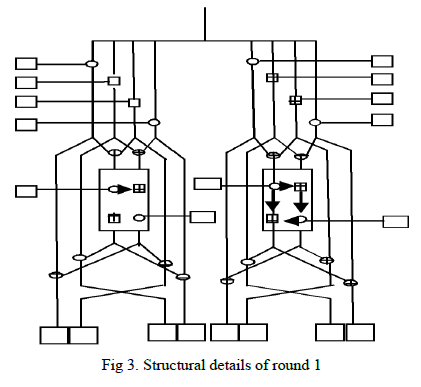 |
| From fig.1and fig.3 following relations can be written: |
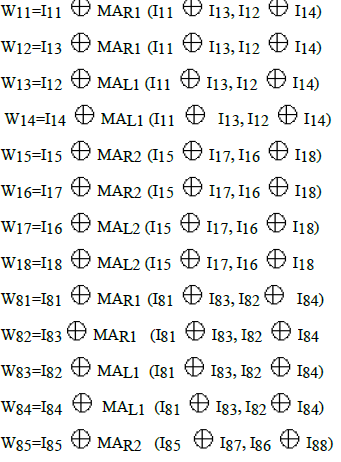 |
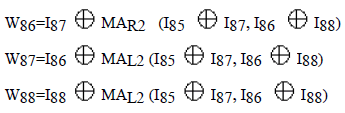 |
| The following relations can be seen from fig.4: |
 |
 |
 |
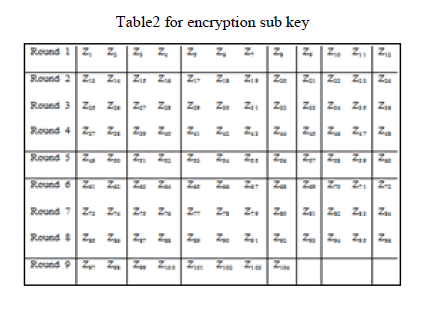
Encryption sub key generation for S-IDEA |
| The sample user key is fed into key generation for each round module which generates 16 sub-keys in each round.Sample user key is also fed into shift logic module that shifts the key by 25 bit circular left shift and again 16 sub-keys are generated.The process is carried out recursively till all 104 sub-keys are generated. |
 |
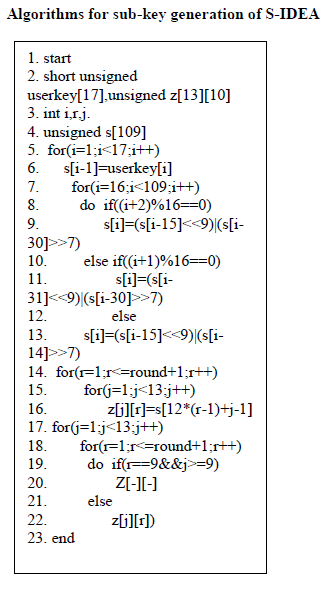 |
Decryption of S-IDEA: |
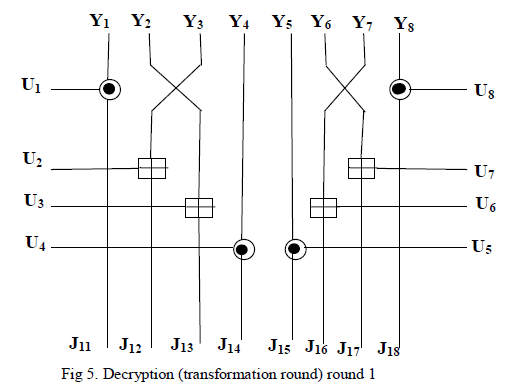
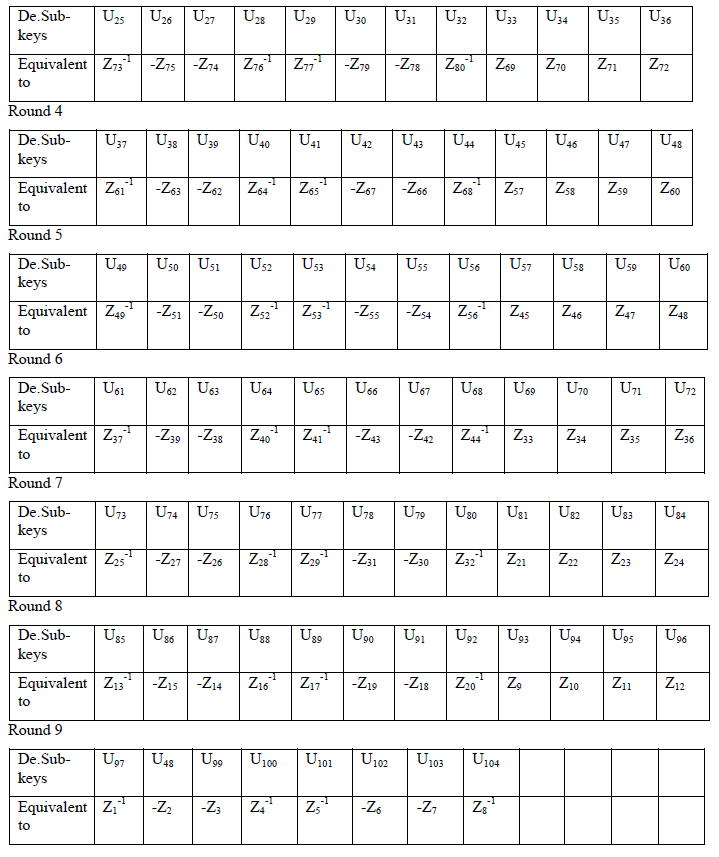
| It implements all the 8+1 rounds of IDEA implementation withall functionalities ( Additive modulo, Multiplicative modulo,Exclusive-OR,MA block etc.) of S-IDEA. Decryption .The decryption process is same as encryption process The output ofeach round is denoted by V whereas the intermediate output undergoing transformation in each round denoted by J. |
Relation between J and W |
| The output of transformation round of decryption (J) is related to output of sub-encryption round of encryption (W) and vice versa. Consider the fig.5.We can write the following relations: |
 |
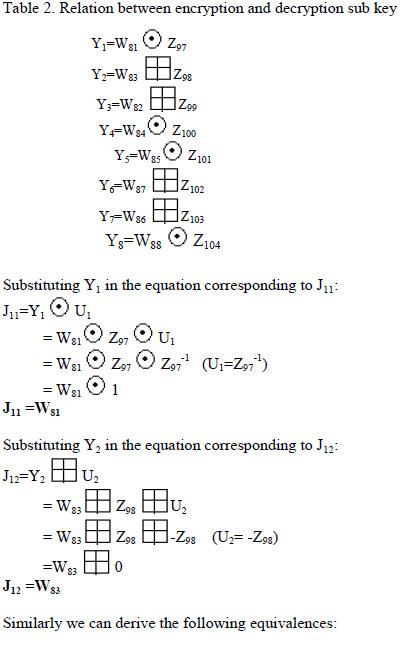 |
 |
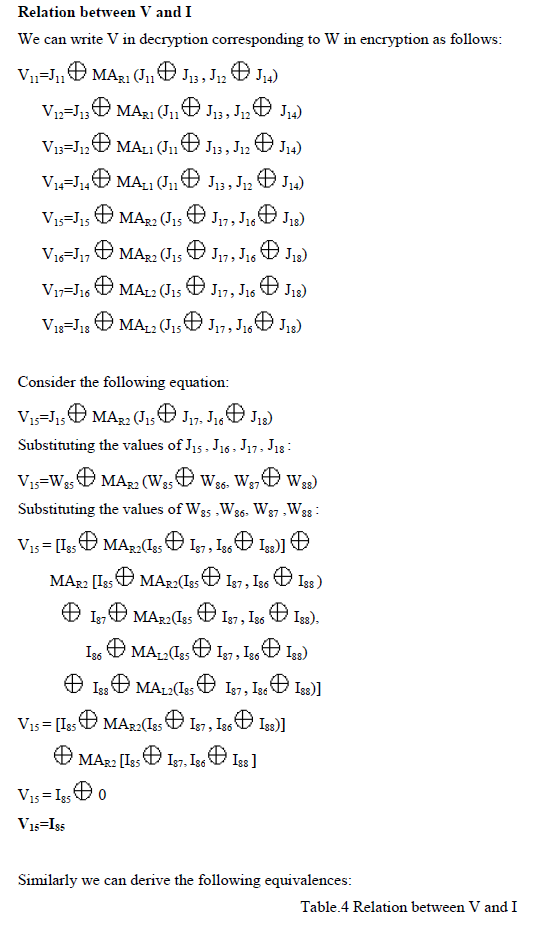 |
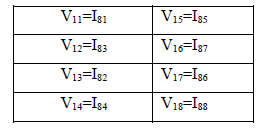 |
 |
 |
 |
EXPERIMENTAL RESULT |
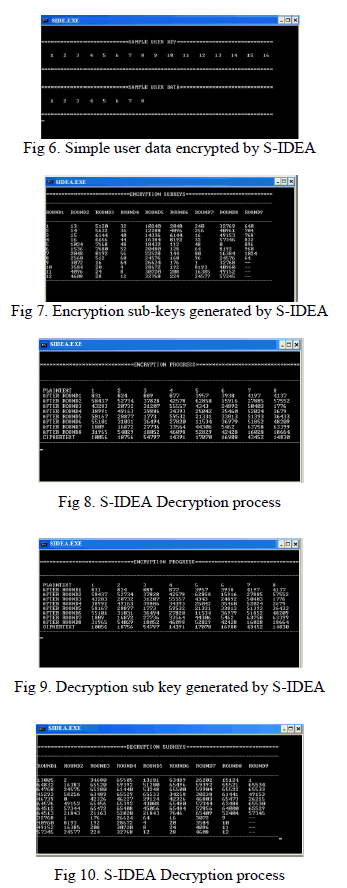
| The result displays in fig. 6 shows the sample user key that is generated in the proposed algorithm. From the user key all 104 sub-keys are generated by the algorithm. It also displays the sample user data generated in the algorithm which has to be encrypted using S-IDEA. |
| Fig.7 depicts 104 encryption sub-keys generated by the proposed algorithm from sample user key. It also shows which sub-keys will be used in which encryption round. |
| Fig. 8 shows the progress of S-IDEA Encryption process. It shows the data encrypted after each round and finally the cipher text is given as the output |
| Fig 9, shows the 104 decryption sub-keys generated by the algorithm from encryption sub-keys. It also shows which sub-keys will be used in which decryption round. |
| Fig 10 ,shows the progress of S-IDEA Decryption process. It shows the data decrypted after each round and finally the plain text is given as the output. |
 |
CONCLUSION AND FUTURE WORK |
| The basic aim of this paper is to increase the strength of existing IDEA algorithm. The proposed algorithm International data Encryption algorithm (S-IDEA) has two key features:-increased key size (256 bits) and increased degree of diffusion (two MA blocks are used in a single round instead of one). The 104 sub-keys are being used as compared to 52 sub-keys previously which enhance the complexity of confusion. Therefore the probability of other forms of attack is reduced due to amount of work that has to be carried out when 104 sub-keys are involved. Addition of a new MA block in each round of SIDEA has contributed to an increase in complexity of diffusion. It makes the algorithm more secure and less susceptible to cryptanalysis. |
| The proposed algorithms increased the cryptographic strength and eliminate the shortcoming of the existing International data Encryption algorithm (IDEA).The future scope of S-IDEA algorithm is that it can also be implemented in hardware using VLSI technology. |
References |
|