International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

2D GEOMETRIC SHAPE AND COLOR RECOGNITION USING DIGITAL IMAGE PROCESSING

Sanket Rege, Rajendra Memane, Mihir Phatak and Parag Agarwal
UG Student, Dept. of E&TC Engineering, PVG’s COET, Pune, Maharashtra, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The paper discusses an approach involving digital image processing and geometric logic for recognition of two dimensional shapes of objects such as squares, circles, rectangles and triangles as well as the color of the object. This approach can be extended to applications like robotic vision and computer intelligence. The methods involved are three dimensional RGB image to two dimensional black and white image conversion, color pixel classification for object-background separation, area based filtering and use of bounding box and its properties for calculating object metrics. The object metrics are compared with predetermined values that are characteristic of a particular object’s shape. The recognition of the shape of the objects is made invariant to their rotation. Further, the colors of the objects are recognized by analyzing RGB information of all pixels within each object. The algorithm was developed and simulated using MATLAB. A set of 180 images of the four basic 2D geometric shapes and the three primary colors (red, green and blue) were used for analysis and the results were 99% accurate.

Keywords
Bounding Box, Extent, MATLAB, Rotation Compensation, Shape and Color recognition.

INTRODUCTION
In today’s highly advanced and automated industries, highly efficient methods are used for various production and inspection processes. There was a time when banal jobs, like quality inspection, sorting, assembly, painting, packaging etc., were done manually. But after the rapid involvement of the field of robotics, the automation industry has undergone a complete makeover.
The sensors play an important role in presenting information related to the parameters in a running process. Temperature, light, percentage composition, humidity, structure shape, dents etc. are the many examples of parameters that sensors can detect. Highly precise sensors are used in industries to provide better feedback to controllers. For example, the more the precision of the sensors, the more is the ability of the sensor to detect a flaw.
The field of Digital Image Processing has found many applications in the field of automation. Sensors like cameras acquire live video feed or image of the objects moving on the conveyer belt. The video or image is then used to recognize the object, or in some cases, compare the object with a predefined, flawless and expected object and a decision is made based on the degree of similarity between the two images. A controller controlling a robotic arm then either allows the qualified object to pass or picks and places the unqualified object into the rejected bin.
This paper attempts to demonstrate the recognition of basic geometrical objects using an algorithm that extracts information from the image at hand (i.e. the second method) and makes decisions on the basis of a few metrics as will be explained in detail.

LITERATURE SURVEY
A number of shape recognition algorithms have been proposed in the past. A detailed survey of shape recognition algorithms can be found in [1], [2].Object recognition can be done in two ways: (1) Comparing every pixel in the image to the pixels of a number of other images stored in the processor’s memory [3], [4], and (2) Extracting information from the image, calculating certain metrics based on this information and comparing the values of these metrics to predetermined values [5]. The first method is commonly used in applications like fingerprint recognition where a large database of fingerprint or facial image samples is maintained in image form. This process is, as expected, memory intensive as well as time consuming for obvious reasons. The second method, on the other hand, is useful when there are limitations on memory as well as time required to process data and produce results.

ALGORITHM
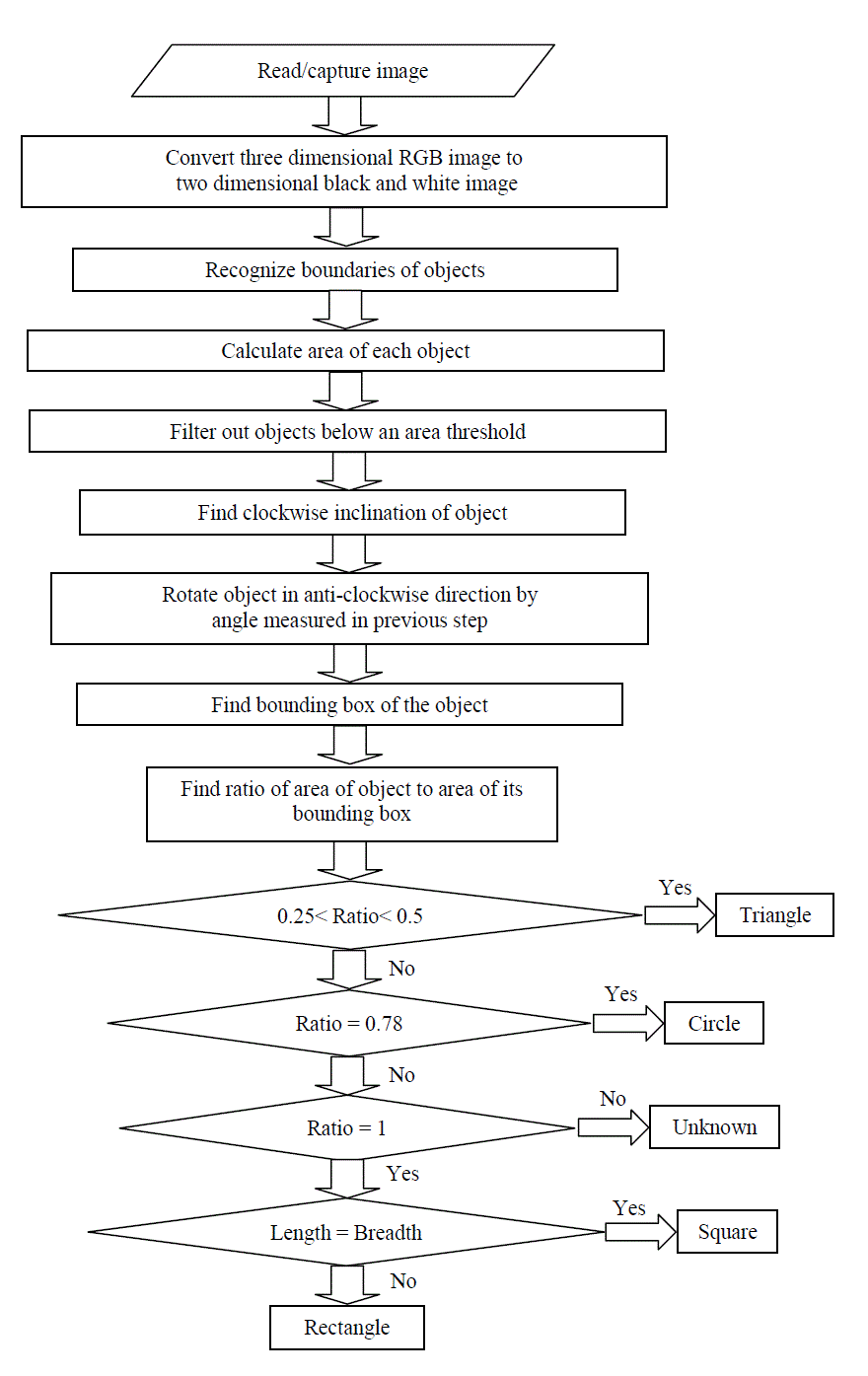
A. Read/capture image
The image is first acquired from a live video feed or an existing image can be loaded from the memory. We shall consider that the acquired image is in RGB format which is a true color format for an image [6], [7]. In MATLAB, the captured or imported RGB image is three dimensional and each pixel is represented by an element of a matrix whose size corresponds to the size of the image.
B. Converting RGB image to Black and White
This process is done in two steps. The RGB image is first converted to a two dimensional grayscale image. The grayscale image is nothing but a matrix that holds the luminance (Y) values of the image [8]. We obtain the luminance values of the image by combining the RGB values using the NTSC standard equation (1) that multiplies the primary colors (red, green and blue) with coefficients based on the sensitivity of our eyes to these colors as shown:
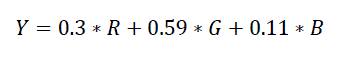equation (1)
The luminance image is then converted to black and white (binary) image by a process called thresholding [9], [10]. A threshold is set and the luminance of each pixel is compared with this threshold. All values that are greater than this threshold are replaced with a logical one (white) and the values below this threshold are replaced by a logical zero (black). The threshold can be calculated either by determining the luminance values of pixels that correspond to object regions in a sample image (i.e., by machine training) and then averaging these values resulting in the threshold, or by using an algorithm that evaluates the histogram of the image and maximizes the variance of intensity between objects and backgrounds [11], [12], [13].
C. Recognize boundaries of objects
The image is now a two dimensional array with binary elements. Boundaries of the objects are recognized by first setting a single pixel on the object-background interface as a starting point and moving in a clockwise or counterclockwise direction and searching for other object pixels. The pixels may be searched either diagonally (in 8-connected pixels) or edge-adjacent pixels (in 4-connected pixels). By hunting for object pixels in a fixed direction, the object’s boundary can be recognized [14].
D. Finding areas of objects and area filtering
Once the object boundaries have been recognized, the area of that object can easily be calculated by summing the number of pixels within the boundary extent.
Very minute objects correspond to noisy pixels that may have been treated as object pixels during the thresholding process. It is necessary to remove these pixels before further processing. By using an if-else condition, those objects whose areas are below a threshold value, can be converted to background pixels (i.e., they can be inverted). In this way the image is filtered to remove small, isolated noise pixels.
E. Finding inclination of object
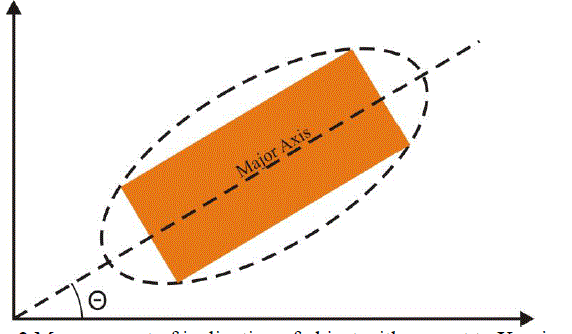
The algorithm must be able to recognize the shape of the object irrespective of the inclination of the object in the plane perpendicular to the camera’s axis. This is usually done by enclosing the object’s four extreme corners in an ellipse and then measuring the counter-clockwise angle (?) between the major axis and the x axis as shown in fig. 2. The object is then rotated in clockwise direction by the same angle.
For squares and circles, the major and minor axes are the same. In MATLAB, the value of this angle is obtained by using the Orientation option under the regionprops command. This procedure is required for aligning the object with the bounding box that will be constructed in later steps.
F. Finding bounding box of the object
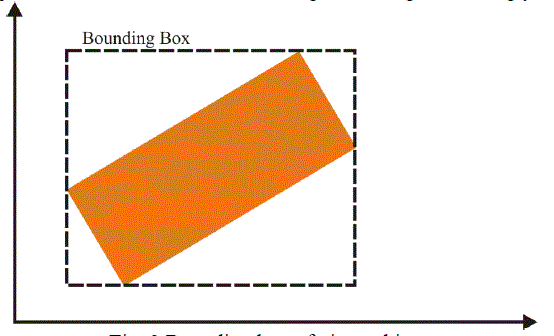
The bounding box of an object is an imaginary rectangle that completely encloses the given object and its sides are always parallel to the axes. Fig. 3 illustrates the concept of a bounding box. It is worth noting that due to the various angles of inclination of an object, the dimensions of the bounding box change accordingly.
However, to make the shape recognition independent of the rotation of the object, the dimensions of the bounding box must be constant. This is because the area of the bounding box is an important parameter which we will be using to classify the shape of the object. This is precisely the reason why we rotate the object in the opposite direction by the angle of orientation as mentioned in the previous step. Therefore we ensure that irrespective of the orientation of the object, we can construct a bounding box of constant dimensions. This method works well with squares, circles as well as rectangles. However, triangles require a different type of treatment as will be shown shortly.
G. Finding ratio of areas for given object
The next step involves finding the ratio of the area of an object to the area of its bounding box (2). In MATLAB, this ratio is known as the Extent and is a very useful parameter:
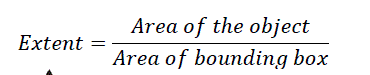equation (2)
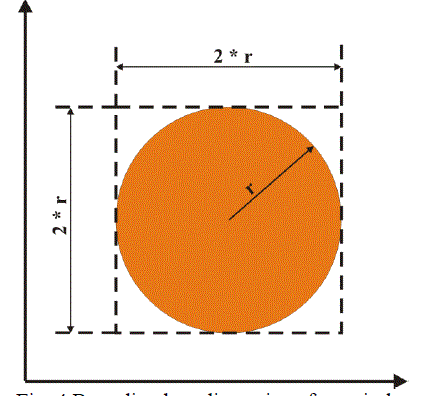
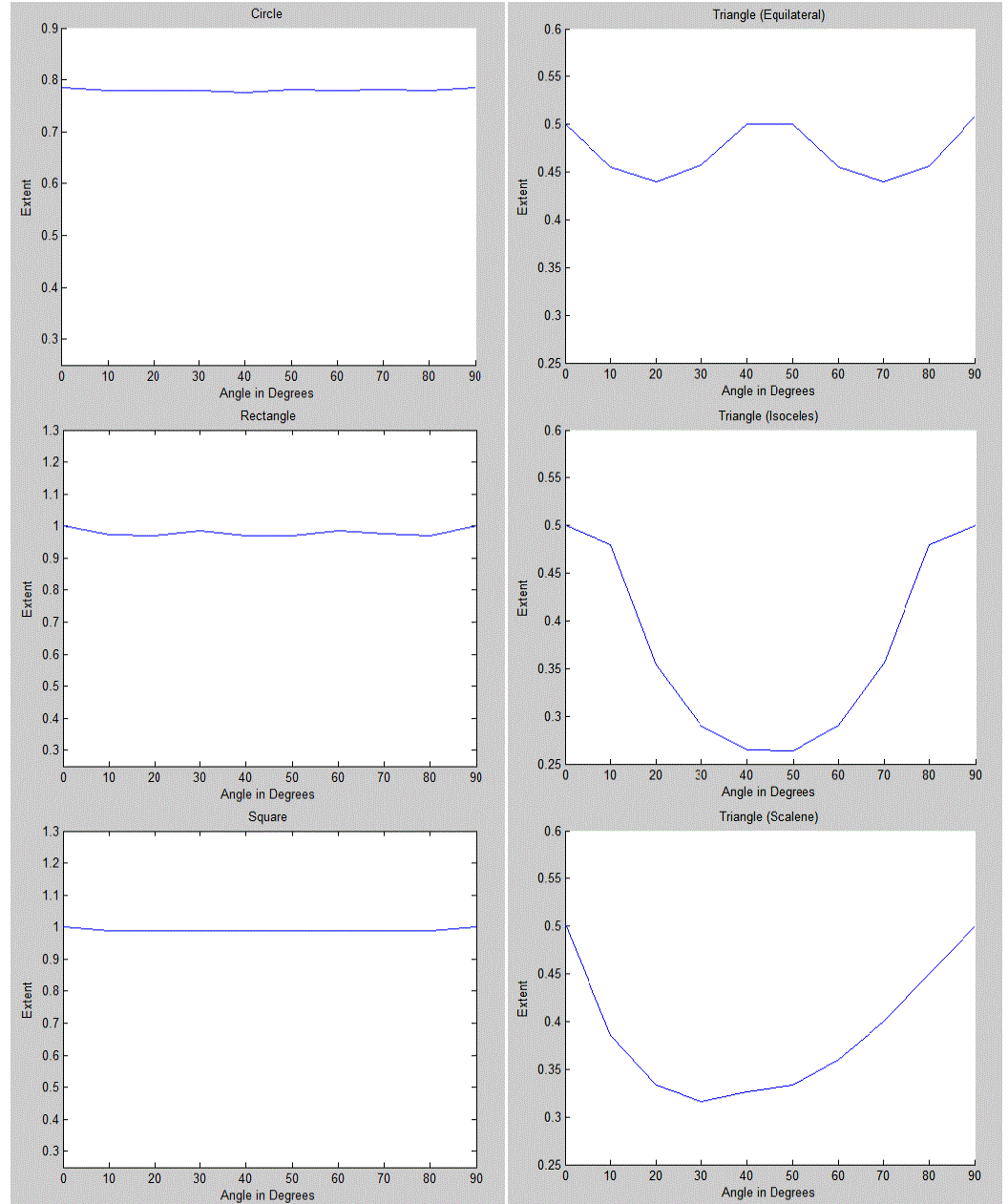
For circles, this value is fixed at 0.7853, irrespective of the radius. The corresponding value for rectangles and squares is 1.0000, provided the sides are parallel to the axes and the bounding box and sides overlap. The following fig. 5 show the values of Extent (Y-axis) plotted against the original inclinations of the objects (X-axis).
The objects were first made independent of rotation by earlier mentioned method. As a result, the value of Extent is seen as constant. Thus, whenever an object that has value of Extent equal to 0.7853 is a circle. Further, whenever an object is encountered that has value of Extent equal to 1.0000, the object may be a square or a rectangle. The decision between square and rectangle can be made on the basis of the dimensions of the object. The object with equal sides is obviously a square. The object with 2 unequal pairs of sides is obviously a rectangle.
For triangles, it is difficult to find the correct inclination as the existence of only three vertices makes construction of a single ellipse (and therefore a major axis), impossible. Therefore, the method fails in this case. However, a basic geometrical rule tells us that a triangle always divides the area of an enclosing rectangle into two halves. Thus the value of Extent must always be less than 0.5000. As seen in the fig. 5 above, for triangles the Extent value ranges from 0.5000 to 0.2500, for given values of initial inclination. Thus, whenever an object is encountered that has value of Extent equal between 0.5000 and 0.2500, the object must be a triangle.
H. Color recognition
The objects may be further evaluated for their colors. This is done by averaging the RGB content within the boundaries of the objects. For example an object with a relatively high average value of R over its surface, may possess a shade of red. In MATLAB, the impixel command can be used to acquire the RGB information in a 1 X 3 matrix over the entire object surface which can be averaged. Using the principles of additive mixing, a large number of colors can hence be recognized.

RESULTS
The algorithm, when tested on a database of fifteen images per shape per color, proved to be accurate with 99% correct results. The database consists of images of the objects having the four shapes and three colors with various inclinations. Table 1 shows the results of the algorithm when run on each image separately.
The images must be taken in a well lit environment (be natural or artificial lighting) and care must be taken to avoid shadows of the objects as much as possible. This is because the thresholding process may consider the shadow as part of the object and as a result, the value of Extent may be wrong. This will obviously affect the shape recognition and results will vary.

CONCLUSION
The algorithm discussed in this paper is a simple, yet effective method of analyzing the shapes and colors of objects. The concept of recognizing shapes on the basis of easily obtainable metrics has been extensively used by us in our research on recognition of breast cancer cells from a given tissue sample. In our research, the algorithm was used to recognize the shapes of all cells and the Extent parameter of normal healthy cells was noted. As cancer cells differ from healthy cells in terms of shape as well as color, their Extent values as well as RGB content do not match those of healthy cells and can therefore be easily identified and quantified.
The applications are not restricted to the bio-medical field but can extend to any field that requires classification of different objects based on their physical appearance. This may include quality inspection in assembly lines, artificial robotic intelligence, computer vision, recognition of vehicles at toll booths or traffic signals for traffic status determination, etc.
 

Tables at a glance
Table icon
Table 1
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
 
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10
 
Figure 1
Figure 11
 

References