δ(δg)*-Closed sets in Topological Spaces

Abstract

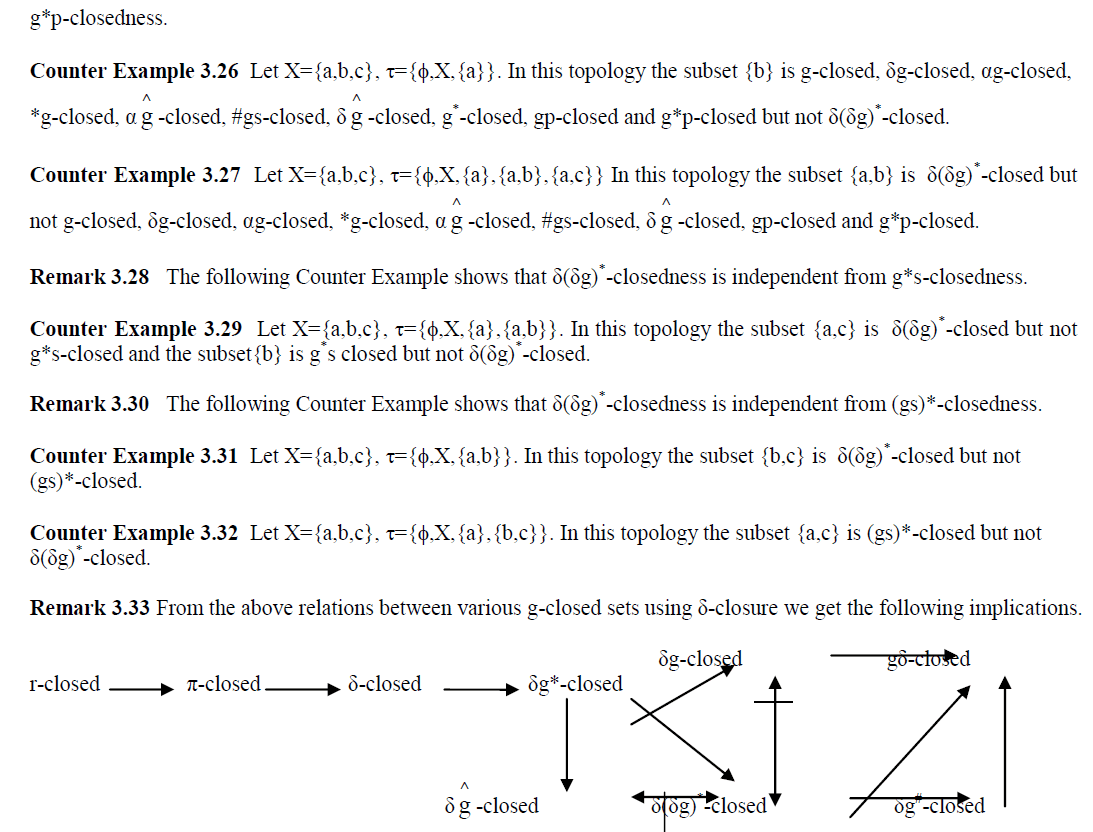
In this paper we introduce and study a new class of generalised closed sets called δ(δg)*-closed sets in topological spaces using δg-closed sets. Moreover we analyse the relations between δ(δg)*-closed sets and already existing various closed sets. It is independent of δg-closed sets and weaker than δg*-closed sets. The class of δ(δg)*- closed sets is properly placed between the classes of δg*-closed sets and δg# -closed sets and a chain of relations is proved as follows. r-closed  π-closed  δ-closed  δg*-closed  δ(δg)*-closed  δg#-closed  gδ-closed

Keywords

g-closed sets, δg-closed sets , δg*-closed sets and δ(δg)*-closed sets.

I. INTRODUCTION

II.PRELIMINARIES

The complements of the above mentioned sets are called regular closed, semi closed, - closed, pre- closed, Semi pre closed, π-closed and δ-closed sets respectively.

The intersection of all regular closed(resp.semi-closed ,-closed, pre-closed, semi pre-closed, π-closed and δ-closed) subsets of (X, ) containing A is called the regular closure(resp.semi-closure, -closure, pre- closure, semi pre closure, π-closure, and δ-closure) of A and is denoted by rcl(A) (resp. scl(A) cl(A), pcl(A), spcl(A), πcl(A), and δcl(A) ).

References

1. [1] Levine, N. (1963), Semi-open sets and semi-continuity in topological spaces, Amer. Math. Monthly., 70, 36 – 41.
2. [2] Levine, N. (1970), Generalized closed sets in topology, Rend.Circ.Math.Palermo, 19, 89 – 96.
3. [3] Velicko,N.V.(1968), H-closed topological spaces, Amer. Math. Soc. Transl., 78, 103-118
4. [4] Dontchev,J.&Ganster.M.(1996),On δ-generalised closed sets and T3/4 spaces,Mem.Fac.Sci.Kochi.Univ.Math.17,5-31.
5. [5] Palaniappan N and KC Rao (1993) Regular generalized closed sets. Kyungpook Math. J 33: 211-219.
6. [6] Maki H, R Devi and K Balachandran (1994) Associated topologies of generalized -closed Sets and α-closed sets and α-generalized closed sets. Mem. Fac. Sci. Kochi Univ. (Math) 15: 51-63.
7. [7] Maki H,J.Umehara &T.Noiri (1996)Every topological space is pre-T½ .Mem Fac Sci Kochi Univ Ser.Alath17, 33-42.
8. [8] Gnanambal.Y(1997)On generalized pre regularclosed sets in topological spaces.Ind.J.Pure.Appl.Math.28(3):351-360.
9. [9] Julian Dontchev,I.Arokiarani and Krishnan Balachandran(1997) On generalised δ-closed sets and almost weakly Hausdorff spaces. Topology Atlas