Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

A Comparative Novel Method of Tuning of Controller for Temperature Process

E.Kalaiselvan1 and J. Dominic Tagore2
  1. Associate Professor, Department of E.I.E, M.A.M College Of Engineering, Trichy, Tamilnadu, India
  2. Project Assistant, Department of E.I.E, M.A.M College Of Engineering, Trichy, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper proposes a novel approach based on analysis of comparative of various tuning used for PID controller with the help of simulation aspects for the design of temperature control process. The purpose of following the PID tuning is due to its simple control structure and satisfactory results. Comparisons between some of the techniques have also been provided and choose preeminent tuning parameters. Apply in real time temperature control of the experiment set is implemented. The simulation is completely done using MATLAB. This various tuning approach would be advantageous for the future industries those who work with PID controller. Finally, real time temperature control of the experiment set is implemented using the same parameters. And the results are discussed. The main goal of this paper is to improve the control action of controller and provide an extensive reference source for people working in PID controllers for temperature process.

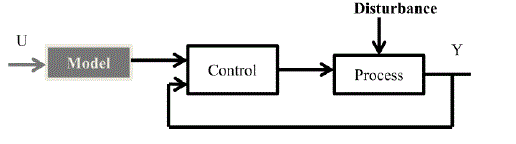
Keywords
Transfer function, PID controller, tuning of PID controller, error criteria- IAE, ISE, ITAE, temperature control.

INTRODUCTION
In general, PID controller is a generic control loop feedback mechanism which is used to calculate the error values. It calculates the error values by means of measuring the difference between process variable and set point [1]. A PID controller is a simple three-term controller where Proportional, Integral and Derivative. Proportional depends upon the present error, and its offset is more. Integral depends on past error, where it can overcome the offset but it overshoots value is more. Derivative depends upon the future error but it can overcome both offset and overshoot, but it cannot be used separately [3]. The output of controller is given by
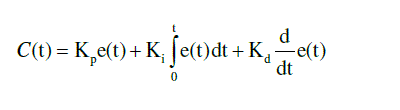equation (1)
Kp = Proportional gain
Ki = Integral gain(Kp /τi)
Kd = Derivative gain (Kp *τd)
C(t) = Controlling signal.
e(t) = error signal with respect to time
Matlab based real time control is realize in this study, to control the temperature of the experimentation set is more realistic [12]. This software could be used for training continuous control modes such as Proportional control, Proportional Integral control and PID control, the paramount of all control modes. Arithmetical equations used to describe these modes have been solved using MATLAB program. Separate algorithms and MATLAB program have been developed for all these control modes. 2D plots enclose been generated in support of visualization of controller output.

TEMPERATURE MODEL KIT DETAILS
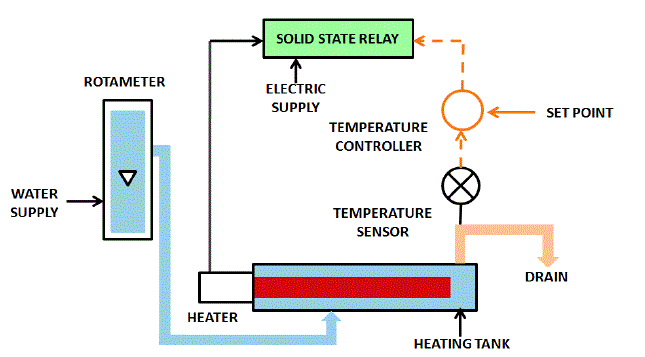
Temperature control trainer is premeditated for understanding the fundamental temperature control principles. The process setup consists of heating tank fixed with SSR controlled heater for on-line heating of the water. The flow of water can be manipulated and measured by rota meter. Temperature sensor (RTD) is used for temperature sensing. The process parameter (Temperature) is controlled by microprocessor based digital indicating controller which manipulates heat input to the process. These units along with necessary piping and fitting are mounted on support frame designed for tabletop mounting. The controller can be connected to computer through USB port for monitoring the process in SCADA mode. Fig. 2.1 show Process diagram of Temperature control Trainer. Table 2.1 shows that some valuable Specification of Temperature Control Trainer

DERIVATION OF TRANSFER FUNCTION
In general, a transfer function relates two variables in a physical process; one of these is the cause (forcing function or input variable) and the other is the effect (response or output variable) [1]. It provides valuable insight into process dynamics and the dynamics of feedback systems. This temperature process is a first order dead time process. So it can be defined as
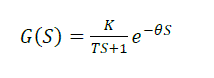equation (2)
Where,
K = Gain constant (B/A)
θ = Delay time
Τ = Time constant
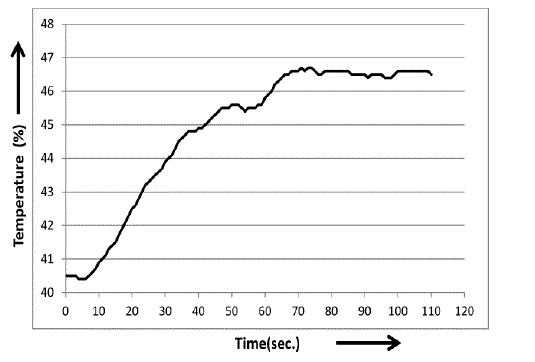
In open loop response, set controller input value and obtain the initial and final steady state value shows in Table 4.1. And note down change of process value with respect to time from initial steady state to final state. Its show in figure 4.1
From Open loop Response, by using those parameter, Delay time ( ) = 7 sec, Gain (K) = 1.1481, Time constant = 35 sec obtain from the graph. eqn. (3) show that open loop response of real time temperature process.
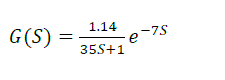equation (3)

APPROACH TO PID TUNING
Tuning a control loop is the adjustment of its control parameters (gain/proportional band, integral gain/reset, derivative gain/rate) to the optimum values for the desired control response [2]. Generally stability of response is required and the process must not oscillate for any combination of process conditions and set points [3]. The following PID tuning formulas are considered:
A. Ziegler–Nichols (Z–N) method (1942): It’s depends on the ultimate gain Ku and the ultimate period Tu. .
B. Tyreus-Luyben tuning method (1992): It’s depends on the ultimate gain Ku and the ultimate period Tu.
C. Cohen–Coon (C–C) method (1953): Based on Process reaction curve. A model with one tangent and point is derived first to tune the PID controller.
D. Shinskey tuning method (1990): This method be worked under the conduction (τ/θ =1.6).
E. Fruehauf tuning method (1990): This method be worked under the conduction (θ/τ <0.33).
F. St. Clair tuning method (1987): Based on Process reaction curve.
Tuning parameters of PI and PID controller are show in Table 4.1 & 4.2

TIME DOMAIN SPECFICATION
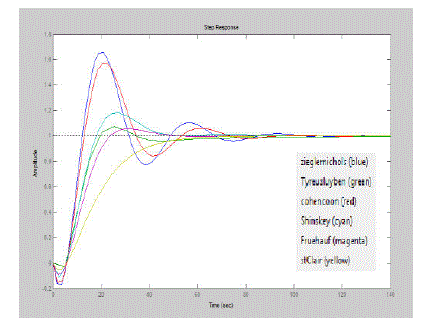
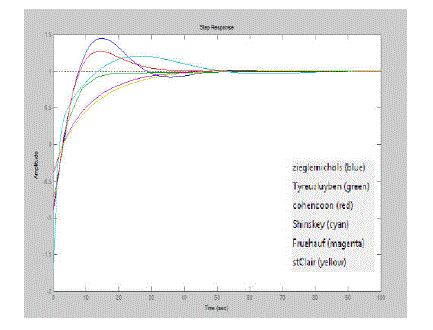
The performance of a control system is typically measured in provisions of its response to a step input. So that by calculating time domain specification of a response its easy analysis. By comparing with various tuning methods in PI controller Tyreus-Luyben and Fruehauf tuning methods shows good response to this system. It shows in table 5.1. In comparisons of PID controller explain in table 5.2 Tyreus-Luyben show good response.

PERFORMANCE ANALYSIS
The integral error is generally accepted as a good measure for system performance [1]. It is useful to have criteria that put little weight on the initial error. These integrals are finite only if the steady- state error is zero. Unlike simple criteria that use only isolated characteristics of dynamic response, the criteria of the category are based on the entire response [9]. The followings are some commonly used criteria based on the integral error for a step set point or disturbance response
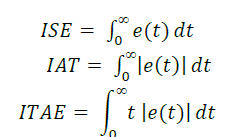equation (4)
Where, e(t) = ysp(t) – y(t) is error of response from the desired set point.
Comparison of integral error of various tuning methods for PI controller and PID controller shows in Table 6.1 and Table 6.2. Here also that Tyreus-Luyben tuning method shows that minimum error for both PI and PID controller.

SERVO AND REGULATION PROBLEM
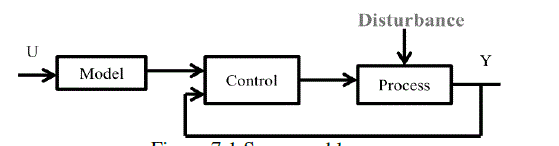
In feedback close loop system; Servo control loop is one which responds to modify in set point where as the load disturbance value remains stable show in figure 7.1. The set point may be changed as a function of time (typical of this are batch processes), and therefore the controlled variable must follow the set point. A regulatory control loop is one which responds to a modify in load disturbance value, bringing the system back to steady state where as the set point value remains stable show in figure 7.2. Regulatory control is by distant more common than servo control in the process industries.

SIMULAION RESULT
The MATLAB coding of the simulator is design various types of function block [6]. The coding is totally based on the concepts of PID tuning. It is that much efficient to analysis any system and give step response using P, PI, &PID controller.
A. Step Response Of Transfer Function in MATLAB Program :
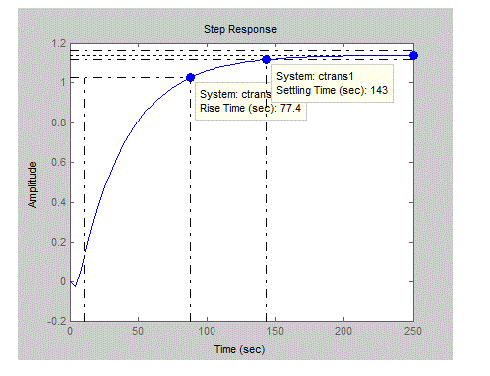
Figure 8.1.1 shows that step response of open loop system for transfer function of
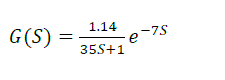equation (3)
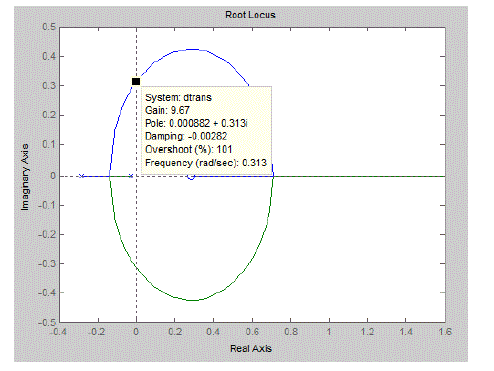
B. To Find Ultimate Gain Ku and Ultimate Time Period Tu in MATLAB Program Using Root Locus Plot
For same transfer function from figure 8.2.1 we get value that shows in Table 8.2.2
C. Response of PID Controller in both MATLAB Program and Simulink Diagram
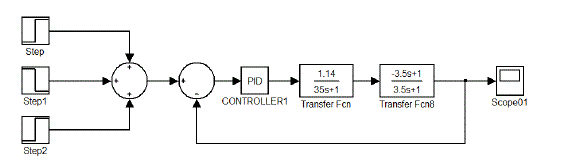
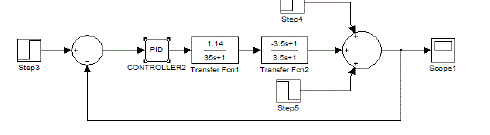
D. Simulink diagram of servo problem and regulatory problem
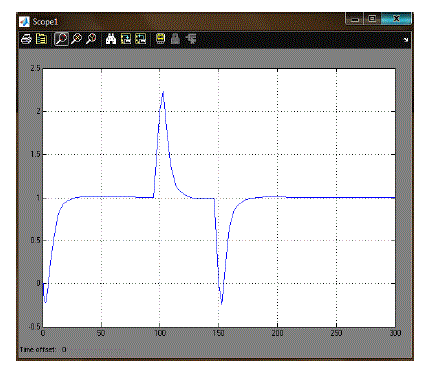
From these analyses of various tuning method we proposed that Tyreus-Luyben tuning methods show the stability proper response. Then apply tuning parameter of Tyreus-Luyben in servo and regulator problem. Figure 8.4.3 and Figure 8.4.4 are shows that analysis of the stability of the system. Here the MATLAB Simulink diagram for the for the servo and regulator problem is show in Figure 8.4.1 and Figure 8.4.2 Since the set point has to be varied the number of step input is declared by giving the different inputs and different sampling time. The value is given as 1,-1 &1. And the output is controlled. For the disturbance rejection the load has to be varied. So the different types of load are given before the output. The disturbance is declared as 1,-1. And the resultant output is given below.

IN REAL TIME IMPLEMENTATION
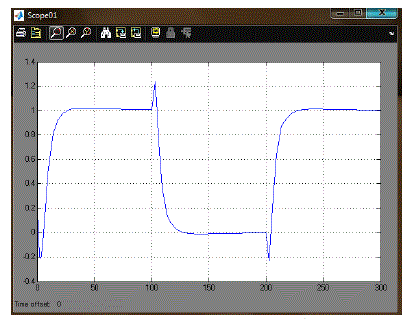
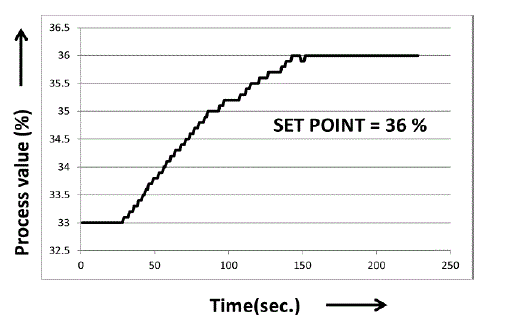
Figure 9.1 shown is the real time response of temperature kit process value. Here tuning parameter of Tyreus- Luyben tuning method value is substituted. The set point is given as 36, when the process variable is less than that of the set point the output reaches maximum value of 100%. After process value reach the set point value controller output will decrease.
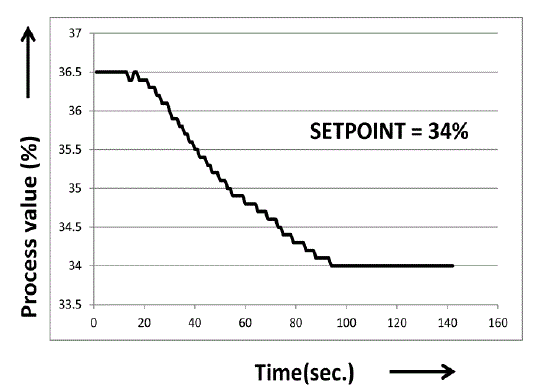
Figure 9.2 shows that set point variation of real time implementation. The old set point value is 36.5 and new set point value is 34. Output response shows that proper controlled comeback.

CONCLUSION
In this paper we proposed comparative novel methods of various types of PID tuning for temperature process and result of comparison also elucidated. A comprehensive comparative study of various types of tuning methods tested with simulation under different conditions show that better analysis. Simulation results have been given to show the performance of the method. The proposed tuning method is superlative and show good performance in apply with real time implementation.
 

Tables at a glance
Table icon Table icon Table icon Table icon Table icon
Table 2.1 Table 3.1 Table 4.1 Table 4.2 Table 5.1
 
Table icon Table icon Table icon Table icon Table icon
Table 5.2 Table 6.1 Table 6.2 Table 8.1 Table 8.2.2
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 2.1 Figure 3.1 Figure 7.1 Figure 7.2 Figure 8.1.1
 
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 8.2.1 Figure 8.3.1 Figure 8.3.2 Figure 8.4.1 Figure 8.4.2
 
Figure 1 Figure 2 Figure 3 Figure 4
Figure 8.4.3 Figure 8.4.4 Figure 9.1 Figure 9.2
 

References