A COMPARISON BETWEEN PASSIVE & SEMI ACTIVE SUSPENSION SYSTEMS

Abstract

This paper illustrates the mathematical modeling of passive suspension system and the control strategies for semi active suspension system. The Simulink software developed by Matlab is used to evaluate the control characteristics [1], for the same a 2 DOF quarter car model is used. The comparison and evaluation of control result are made using software-in-the-loop simulation (SILS) method. From the result we can see that passive suspension is designed to withstand a particular value of disturbances. Skyhook strategy can provide an improved vehicle ride comfort. Minimax strategy can improve drive safety of vehicle by manipulating wheel load. The skyhook and minimax strategies can be switched to control semi-active suspension system to fulfill different requirement of vehicle in different stages.

Keywords

passive suspension, Semi-active Suspension, software in the loop simulation, quarter car model, control strategies.

INTRODUCTION

The duty of a suspension system is to bear the vehicle weight, to cut off the vehicle body from road disturbances, and to preserve the traction force between the tires and the road surface. The function of suspension system is to advance the comfort of riding, road traction handling and steadiness of vehicles. Suspension systems are classified into a passive, semi-active and active suspension system. We can say ac compromise between the passive systems, and the costly higher-performance fully active suspension system is called semi active suspension system. In consideration with an active system, a semi-active system requires much less power, and is less complex and more consistent and can provide great improvement in ride quality. Karnopp [2] introduced the skyhook control strategy, which is unquestionably the most broadly used control policy for semi-active suspension systems. The skyhook control can decrease the resonant peak of the body mass and thus achieves a good quality riding. But, to improve both the ridequality and the safety of vehicle, both resonant peaks of the body and the wheel need to be reduced. For this purpose Minimax control strategy proposed by Prof. Herman Winner and Tobias Niemz is introduced in this thesis. The models of skyhook and minimax are developed using Matlab/Simulink. The passive suspension, minimax and skyhook are compared using SILS. This paper is prepared as follows. In Section II, a two degree-of-freedom quarter car model for the semi-active suspension system is given. In Section III, on/off skyhook algorithm is introduced. Wheel load influence matrix is introduced and minimax controller is designed. In Section IV, the Simulink models are shown. In section V the performances of passive system, skyhook and Minimax strategies are compared and evaluated using SILS and the simulation results are given.

II. A QUARTER MODEL

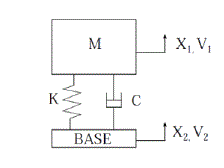Fig.1.A 1DOF passive suspension system quarter car

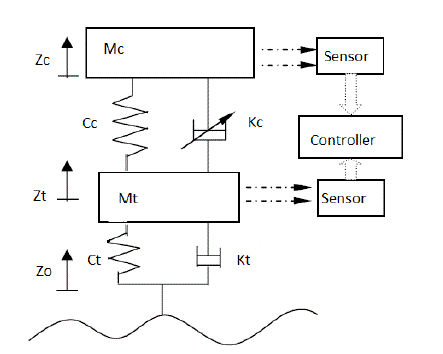Fig.2. A 2 DOF semi active suspension system quarter car

It is known that the ride characteristics of vehicles can be characterized by considering the „quarter-car‟ model [3]. This method has been widely used to examine the working of passive [4], semi-active [5], and fully active [6] suspension system. The quarter models of passive and semi active suspension systems are shown in figures 1 and 2 respectively Here, the semi active quarter car model considers the body mass Mc , wheel mass Mt, , body vertical stiffness Cc , wheel vertical stiffness Ct and damping coefficient of wheel damper Kt . It has two degrees of freedom, body deflection Zc, wheel deflection Zt , and is excited by Zo . The parameters of the model (front left wheel) are shown in Table I. The mathematical model for the above system is as follows

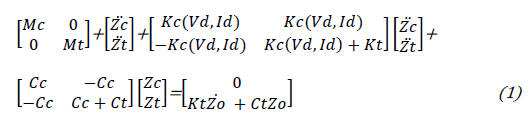TABLE 1 QUARTER CAR MODEL PARAMETERS FOR FRONT LEFT WHEEL

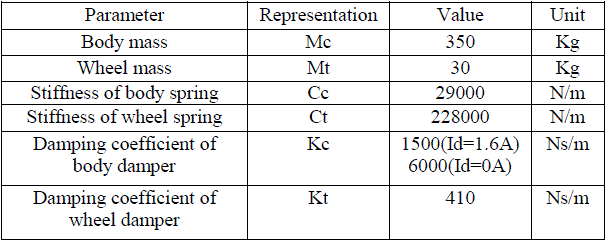According to above mentioned equation the linear differential equations relating the dynamics of the semi-active suspension can be written as:

Here V1 is the absolute velocity of the body V12 is the relative velocity of the body and wheel across the suspension. This strategy indicates that if body velocity and the relative velocity of the body with respect to the wheel is in the same direction, a maximum damping force be supposed to be applied to reduce the body acceleration. On the other hand, if the two velocities are in the opposite to each other, the damping force be supposed to be at a minimum to minimize the acceleration of the body. The main challenge with this control strategy is, it requires the amount of the absolute velocity of body. Even though the exact measurement of the absolute vibration velocity of body on a moving vehicle is very difficult to achieve, it is easy to do for the laboratory experiment in order to evaluate the performance of damper and controller. We use an accelerometer to obtain the acceleration of the body. Body acceleration can be used to find the velocity of the body.

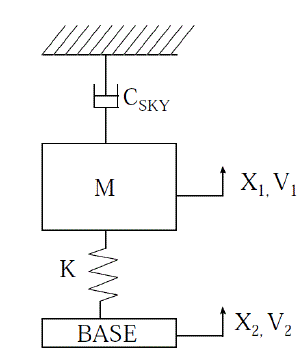Fig.3. Ideal skyhook configuration

B. Minimax Control Strategy

We know safety of the vehicle is highly dependent on wheel load variations. It can be influenced by a damper for that Tobias Niemz presented control algorithm. A Wheel Load Influence Matrix can be induced by considering every possible state of damper movement. Wheel load Influence Matrix is shown below

TABLE 2 WHEEL LOAD INFLUENCE MATRIX

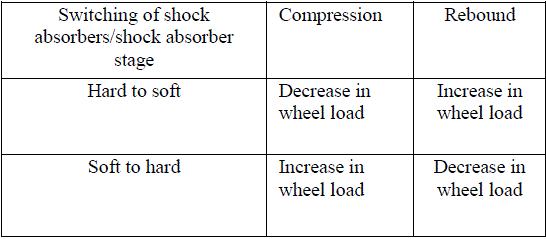The Matrix can be read as following manner: In rebound, if the damper is switched from hard to soft, this will lead to an increase in wheel load. In compression, if the damper is switched from hard to soft, this will lead to a decrease in wheel load. This wheel load influence matrix shows that it is possible to purposely influence the course of wheel load. This knowledge about the effect of switching the damper can be implemented into a switching logic. This logic chooses between the two characteristic lines ´soft´ and ´hard´, depending on the inputs ´damper velocity´ and ´request of wheel load´, and is therefore called Minimax-controller. In Fig. 2, the principle function of the minimax controller is shown. Depending on the inputs VD and Fz,req the damper current ID is switched to either 0 or 1.6A (hard or soft damper). This means if either the request of wheel load or the damper velocity changes its sign, the damper will be switched from hard to soft or vice versa. The damper velocity VD or the sign of the damper velocity sign (VD) provides with Information about the direction into which damper is moving compression or rebound. The request of wheel load Fz, req has values of either one (increase of wheel load) or minus one (decrease of wheel load).

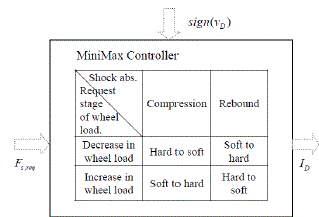Fig.4.Minimax Controller

IV.SIMULINK MODELS

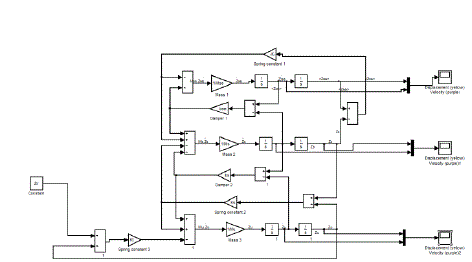Fig.5. passive model

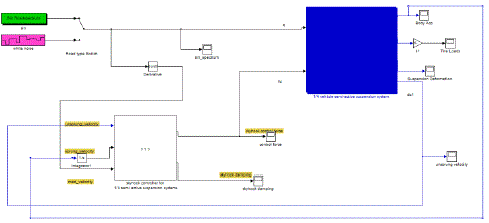Fig.6. skyhook model

V. SILS AND RESULTS

The control model of passive suspension, skyhook and minimax control for semi-active suspension are established in Simulink. SILS are implemented using Matlab/Simulink. In SILS stage of development, components and control algorithms are simulated on an arbitrary computer without real-time requirements to obtain. The simulation results are shown in Fig.7. In order to compare the control performance, they were all excited by sine wave that the amplitude is 1cm. Fig. 7 shows vertical body acceleration response of passive, skyhook and Minimax control. As can be seen from Fig. 7the body acceleration of skyhook control has more reductions than that of passive and minimax control. That means skyhook control can decrease vertical body acceleration effectively and improve ride comfort of vehicle. Wheel load force of passive, skyhook and Minimax are compared in Fig.8. In comparison with passive system and skyhook, drive safety can be improved using minimax controller.

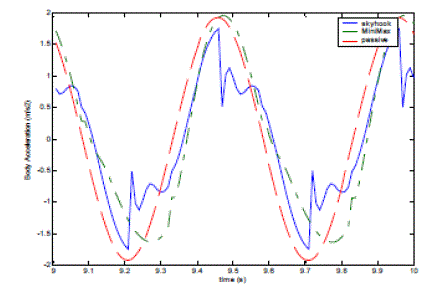Fig.7. Comparison of Body Acceleration reaction of Passive, and Minimax

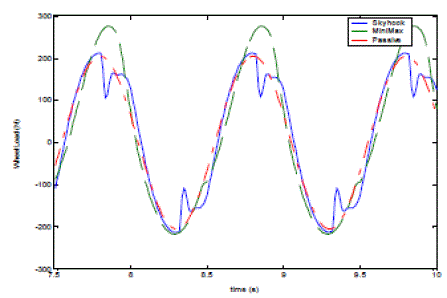Fig.8. Comparison of Wheel Load reaction of Passive, minimax and skyhook

From the results, the conclusion can be drawn that the ride comfort improvement is almost completely owing to the skyhook component. Minimax strategy cans effectively mprove drive safety of vehicle by influencing wheel load.

VI. CONCLUSION

The current paper has described the performance comparison of passive system, control strategies for semiactive suspension systems using SILS method. From the results of simulations, skyhook control can achieves more reduction of resonant peak of the body mass than that of passive suspension and minimax controller and thus gives a good ride comfort. Otherwise, it is possible to purposefully increase or decrease the wheel load by using minimax controller to improve the safety of vehicle. Consequently, skyhook and Minimax strategies can be switched during the vehicle is running in proper moment for effectively improving both riding comfort and safety of vehicle.

ACKNOWLEDGMENT

I would like to thank my guide Dr.Murtaza, professor mechanical engineering department, The Oxford College of Engineering, Bangalore for his valuable support to develop this project

References

1. [1] Delay,s Matlab&Simulink by mathwork
2. [2] Karnopp, D.C., Crosby M.J. and Hardwood, R.A.,”vibration control using semi active force generators”
3. [3] Rosheila Binti Darus , Modeling and Control Of Active Suspension For A Full Car Model
4. [4] B.T.Fijalkowski ,”Automotive mechatronics:operational and practical issues”
5. [5] Sergio M. Savares, Charles Poussot-Vassal, Cristiano Spelta , Olivier Sename , Luc Dugard” Semi-Active Suspension Control Design for Vehicles “
6. [6] Peter gaspar, Soltamszabo, Joseph Boker ,” Active suspension in integrated vehicle control”