A Decomposition Algorithm for Solving A Class of Bi-Criteria Multistage Transportation Problem With Case Study

Abstract

In transportation problems with one or multistages, single criterion of minimizing the total cost is usually considered. But in certain practical situations two or more objectives are relevant. For example, the objectives may be minimizations of the total cost, consumption of certain scarce resources such as energy, total deterioration of goods during transportation, etc. Clearly, this problem can be solved using any of the multiobjectives linear programming techniques, but the computational efforts needed would be prohibitive in many cases. The computational complexity in these techniques arises from the fact that each of the methods finds the set of efficient extreme points in the decision space where such extreme points are, generally, many. Therefore, this paper develops a method of finding the nondominated extreme points in the criteria space, for a certain model of multistage transportation problems. This paper presents the mathematical formulation of different bi-criteria multistage transportation problem, and an algorithm for solving a class of them. This class can be solved using the decomposition technique of linear programming utilizing the special nature of the transportation problem and the method of finding the no-dominated extreme points in the criteria space. A case study is included in this paper to find the efficient distribution of wheat and flour in Middle Egypt mill-stones company.

Keywords

Transportation Problem, Multistage Transportation Problem. Bi-Criteria Transportation Problem, Multiobjective Decision Making, Decomposition Technique.

INTRODUCTION

The standard form of the transportation type of linear program with a single objective of minimizing the total cost was first formulated and solved by Frank L. Hitchock and T.C. Koopmans in the 1940s. Multiplicity of criteria is relevant in a variety of linear programming problems. In certain transportation problems two or more objectives are relevant. For example, the two linear objectives may be minimization of the total cost and minimization of the total deterioration. Deterioration is relevant in the case of certain perishable or decaying items. The degree of deterioration may be dependent on the route, mode and time of transportation.

Practically, the transportation processes are done in many stages and the optimal solution for these problems differs when, using the optimal solution for each single stage.

Ivan Brezina and Andriana Istvanikova [1] presented a way of solving two-stage transport problem. Osman M.S.A. and Ellaimoney E.E.M. [2] presented an algorithm for solving a class of multistage transportation problems. Different multistage bicriteria transportation problems can be arise practically depending on the type of transportation whether classical or not, number of stages, the connection between transportations at each subsequent stage and so on.

Intensive investigation on multiobjective linear transportation problems (MOLTP) have been made by several researchers. Aneja and Nair [3] presented a bicriteria transportation problem model. Lee and Moor [4] studied the optimization of transportation problems with multiobjectives. Diaz [5,6] and Iserman [7] proposed the procedures to generate all non-dominated solutions to the MOLTP. Current et al [8] prepared a review of multiobjective design of transportation networks. Ringuest J.L. and Rinks D.B. [9] proposed the interactive solutions for linear multiobjective transportation problem. Recently, Yousria Abo-elnaga et al (2012) [12] introduced a trust region globalization strategy to solve multi-objective transportation, assignment, and transshipment problems. Khurana et al (2011) [13] studied a transshipment problem with mixed constraints. Also. In (2012) Khurana et al [14] they introduced an algorithm for solving time minimizing capacitated transshipment problem.

In this paper formulations of different bicriteria multistage transportation problems, and an algorithm for solving a class of them are presented, this class of bicriteria multistage transportation problems can be solved using the decomposition technique of linear programming [10,11] utilizing the special nature of the transportation problems. The presented algorithm determines the points of the nondominated set in the objective space instead of in the decision space. The method consists of solving the same multi stage transportation problem repeatedly but with different objectives and each iteration gives either a new nondominated extreme point or changes the direction of search in the objective space. Also the method consists of decompose the bicriteria multistage transportation problems into:

- Subproblems corresponding to every stage

- A master program which ties together the subproblems.

Every subproblem constitutes a bicriteria transportation problem, and the algorithm terminates when no more new nondominated extreme point is available.

FORMULATION OF BICRITERIA MULTI-STAGE TRANSPORTATION PROBLEMS

The formulations of different bicriteria multistage transportation problems which are presented in this paper almost cover several real situations. The proposed formulations enable the decision maker discussing such transportation problems to find his goal.

A. BICRITERIA MULTISTAGE TRANSPORTATION PROBLEMS OF THE FIRST KIND (BMTP 1):

This case represents bicriteria multistage transportation problems without any transportation restrictions on the intermediate stages. In order to obtain the mathematical formulation of the problems representing this case let us assume that:

cij: minimum transportation costs between the first stage sources and the last stage destinations.

dij: minimum deterioration of a unit while transporting from first stage sources to last stage destinations.

ai: Availabilities of the first stage sources.

bj: Requirements of the last stages destinations.

xij: Amounts transported from i to j.

Then the problem takes the form:

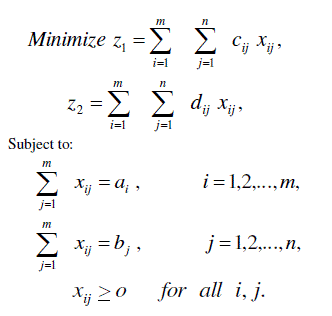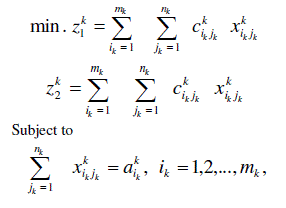C. BICRITERIA MULTISTAGE TRANSPORTATION PROBLEMS OF THE THIRD KIND (BMTP 3):

This case represents bicriteria multistage transportation problems with some additional transportation restrictions on the intermediate stages which does not effect the bicriteria transportation problem formulation at each stage.

The mathematical formulation of the problem representing this case is given us:

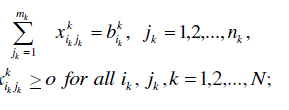D. BICTERIA MULTISTAGE TRANSPORTATION PROBLEMS OF THE FOURTH KIND (BMTP4):

This case represents bicriteria multistage transportation problems in which the subtraction between the input and the output transportation commodity is known at the sources (destinations) of each intermediate stage. The assumed transportation restrictions in this case affect the transportation formulation of each individual stage.

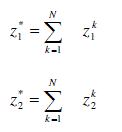(BMTP1) Is solved as a single stage bicriteria transportation problem.

(BMTP2) Can be solved as N single stage bicriteria transportation problems and the nondominated solutions can be obtained from the sum of the solutions for each individual stage.

(BMTP3) Can be solved using the decomposition technique utilizing the special nature of the transportation problems for determining the points of the nondominated set in the objective space.

(BMTP4) Can be solved using any algorithm for solving multiobjective linear programming problems.

An efficient solution for any model is defined as that point in the feasible domain of that model for which there is no other feasible point which dominates it for all the objectives. Its image in the objective space is called a nondominated solution.

In the following we will present an algorithm for determining all nondominated extreme points of the (BMTP3) model from which the solution of the (BMTP1) and the (BMTP2) models can be deduced as special cases from it.

Let: for independent constraints:

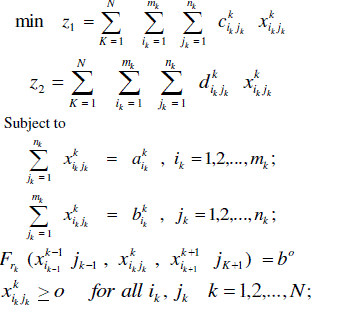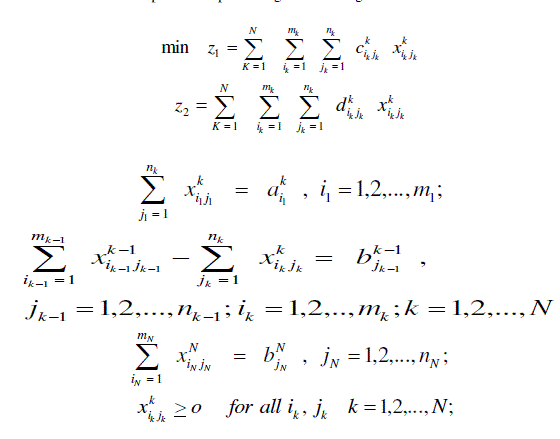Phase II:

Phase II Is the decomposition algorithm which can be found in [2]. Since the special structure of the (BMTP3) model may allow the determination of the optimal solution by, first decomposing the problem into small subproblems and then solving those subproblems almost independently, then the decomposition algorithm for solving large scale linear programming problems utilizing the special nature of transportation problem can be used to solve it.

A. Phase I:

Step 1: Go to phase II, find

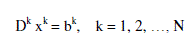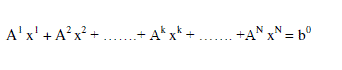B. Phase II:

Step 1: Reduce the original problem to the modified form in terms of the new variables βk

Step 2: Find an initial basic feasible solution to the modified problem.

Step 3: Solve the subproblems

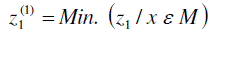Otherwise, go to step 5.

Step 5: Introduce the variable k L βcorresponding to into the basic solution. Determine the leaving variable using the feasibility condition and compute the next B-1 using the revised simplex method technique, go to step3.

A CASE STUDY: EFFICIENT DISTRIBUTION OF WHEAT AND FLOUR IN MIDDLE EGYPT MILLSTONES CO.

A. DATA COLLECTION

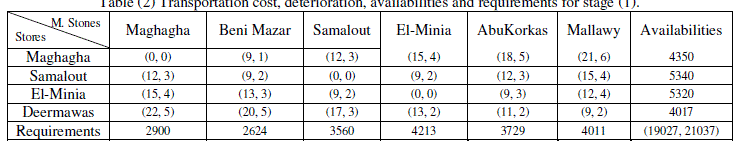
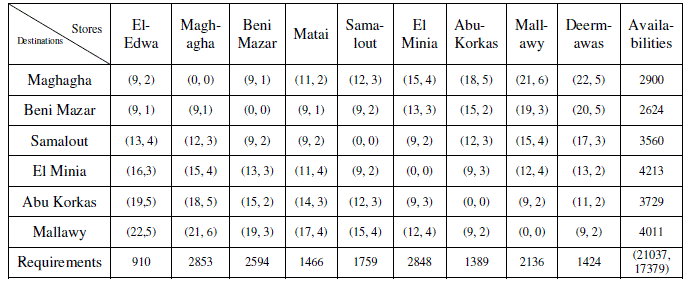
The presented algorithm is applied to Middle Egypt Millstones Company (El-Minia Sector) to obtain the nondominated extreme points in the objective space for transporting wheat and flour. The problem is a bi-criteria two-stage transportation problem to transport wheat and different types of flour between main stores (suppliers) to millstones (warehouses) and finally to destinations (customers). The collected data for transportation cost (LE/ton), transportation deterioration (losses) (LE/ton), availabilities of main sources, requirements of warehouses, and destinations (ton) are presented in Tables (2), (3) for the first and the second stages respectively.

B. APPLICATION RESULTS

The problem is solved by the presented algorithm and Tables (4), (5) illustrate the non-dominated extreme points as well as the efficient distribution accompanying each iteration. Choosing a non-dominated point and its related distribution from Tables (4), and (5) should be done according to the decision maker point of view.

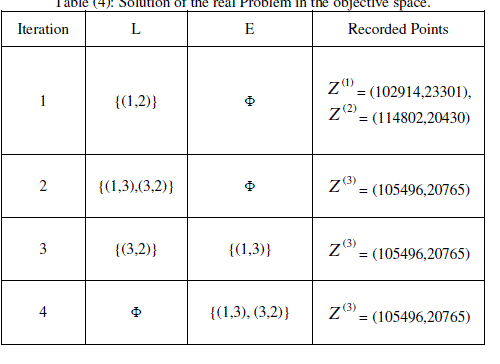CONCLUSION

In certain situations, two objectives are relevant in transportation problems, also, the goods transportation may not operate always directly among suppliers and customers. In such problems, it is possible to optimize the transportation on two stages. The presented algorithm in this paper enables solving such problems more realistically. It can be used for determining all efficient extreme points. The main advantage of this approach is that the bi-criteria two stage transportation problem can be solved using the standard form of a transportation problem at each iteration. From the application, decision maker will have all efficient extreme points and their related distributions. Therefore, he can choose any point which provides his policy.

References

1. [1] Berzina, Istranikova, “The way of solving two-stage transportation problems”, Mathematical Methods in Economics, 39 – 44, 1999.
2. [2] Osman M.S.A., Ellaimony E.E.M., “On bi-criteria multi-stage transportation problems”, Proceedings of the first ORMA conference, pp 143 – 157, 27 – 29 Nov. 1984.
3. [3] Aneja Y.P., Nair K.P.K., “Bi-criteria transportation Problems”, Management Science, vol. 25, pp 1 – 11, , 1979.
4. [4] Lee S.M., Moore L.J., “Optimizing transportation problems with multiple objectives”, AIIE Transactional, vol. 5, pp 332 – 338, 1973.
5. [5] Diaz J.A., “Solving multi-objective transportation problem”, Ekonomicko- Matematicky Obzor, vol. 14, pp 267 – 274, 1978.
6. [6] Diaz J.A., “Finding a complete description of all efficient solutions to a multi-objective transportation problem”, Ekonomicko- Matematicky Obzor, vol. 15, pp 62 – 73, 1979.
7. [7] Isermann H., “The enumeration of all efficient solutions”, Naval Research Logistic Quarterly, vol. 26, pp 123 – 139, 1979.
8. [8] Current J., Min H., “Multi-objective design of transportation networks: Taxonomy and annotation”, European Jornal of Operations Research, vol. 26, 1986,.
9. [9] Ringuest, J.L., Rinks, D.B., “Interactive solutions for the linear multiobjective transportation problem”, Eur. J. Oper. Res. 32, 96 – 106, 1987.
10. [10] Taha H.A., “Operations Research, An Introduction”, Seventh Edition, Prentice Hall, ISBN 0-13-048808-9, 2003.
11. [11] Hillier F.S., Lieberman G.J., “Introduction to Operations Research”, Seventh Edition, Mc Graw-Hill, ISBN 0-07-118163-6, 2001.
12. [12] Yousria A., Bothina E. and Hanadi Z., “Trust region algorithm for multi-objective transportation, assignment, and transshipment problems”, Life Science Journal, 9 (3): Page 1765-1772, 2012.
13. [13] Khurana A. and Arora S., “Solving transshipment problems with mixed constraints”, International Journal of Management Science and Engineering Management, 6 (4): Page 292-297, 2011.
14. [14] Khurana A., Tripti V. and Arora S., “An algorithm for solving time minimizing capacitated transshipment problem”, International Journal of Management Science and Engineering Management, 7 (3): Page 192-199, 2012.