Keywords
|
| stochastic flow networks; capacity; system reliability; genetic algorithm; meta-heuristics. |
| |
 |
ASSUMPTIONS
|
| Following are the assumptions for the rest of the sections |
| 1. All the arcs and nodes have several possible capacities and can fail |
| 2. Two type of commodity are transported / transmitted from s to t. |
| 3. Current capacity xi takes values from {0, 1, 2, …,Mi}, i = 1, 2, …, n+q . |
| 4. The capacities of different components are mutually and statistically independent. |
| 5. Flow of each commodity must conserve Σmj=1 fjk = dk, k = 1,2 |
INTRODUCTION
|
| The reliability of a network is a measure of probability of connectivity between source node s and terminal node t. From the quality management and decision makingpoint of view, it becomes imperative not only to define the load carrying capacity of each node and arc of the network but also to develop some measures in order to evaluate the system performance [1], [2]. Many real life systems such as computer systems, telecommunication systems, transport systems, urban traffic systems, electrical power transmission systems, logistic supply chains and internet etc. fall under the category of flow networks and are mostly linked with performance. In flow networks each transmission line consists of several physical lines between s and t, and each physical line has several successful states and can fail also; hence the capacity of each branch has several values.Such networks are called stochastic-flow networks. The performance of stochastic flow networks, under the condition that each arc flow capacity is deterministic, is not only associated with network reliability but it is also the measure of maximum flow capacity per unit time between sources to terminalt [3]. |
| In a binary-state flow network, the capacity of each branch (the maximum flow passing the branch per unit time) has two levels: 0, and a positive integer. For the perfect nodes case without budget constraint, [4] computed the system reliability, the probability that the maximum flow of the network is not less than the demand, in terms of MP. A MP is an ordered sequence of branches from the s totthat has no cycle. Note that a MP is different from the so-called minimum path. The latter is a path with minimum cost [5]. Researchers in [6], [7] extended the system reliability problem to stochastic flow networks. A stochastic-flow network is also called a multistate network because it is composed of multistate arcs. Themaximum flow between s to t is not a fixed number in these networks. Several authors [8-15] had presented algorithms to generate all minimum paths (lower boundary points) for the demand d in order to evaluate the system reliability. The lower boundary point for d is a minimal system state meeting the demand constraint. The flow networks can allow single as well as multicommodity (multiple types of commodity) to be transmitted through it. Such a network is called a multicommodity capacitated-flow network [5]. Modern systems like a broadband computer network(audio files, video files, multimedia, etc.) and urban traffic controletc. are the examples of multicommodity flow systems. In all such systems the arc capacity / bandwidth is shared simultaneously by multicommodity. The pioneer work in this field is attributed to authors [16], [17], discussed the multicommodity minimum cost flow problem to minimize the total cost of multicommodity by assuming the capacity of each arc is a constant(i.e., the arc is deterministic). Besides, some authors [18], [19] have solved the multicommodity maximal flow problem to find the maximal total flow assuming the arc is deterministic. However, the maximal total flow is not an appropriate performance index especially in case different type of commodity consumes the arc capacity differently [1]. For instance, let’s consider a case of a telecommunication network through which different type of information, like data, audio, video and pictures are transmitted simultaneously from s to t. For clear understanding let’s consider that two commodities, one consisting of 150 data files of 100KB each (commodity 1) and other having 100 video files of 200KB each (commodity 2) have to be routed. Further it is assumed that there exists no direct path between s to t. The each route from s to t must pass through some intermediate nodes. All or any of the arc connecting source to terminal can fail, may be under maintenance or be occupied by some other transportation. Due to multiplicity of routes between source and terminal, the capacity of each arc is multistate. If at least two data packets of each commodity must be transported simultaneously (i.e. d1= 2 and d2 = 2) in the form of packets of 1000KB through the network. It is evident that both the commodities consume different capacities of each branch. It clearly shows that different commodities consume different capacities arcs of flow network.Further there is a budget constraint within that all this transportation has to be accomplished. The cost of transportation is bound to increase with the increase in number of containers. Thus, the objective of the flow networks is to maximise the flow and minimize the cost. |
| The present work proposes a continuous integer genetic algorithm (GA) based model to evaluate the reliability of multicommodity stochastic flow network under budget constraint. The proposed model is motivated from the work of author [3] and is based on two major characteristics 1) each node or arc has several possible capacities and may fail; 2) the capacity weight varies with arc, nodes and types of commodity. To implement the proposed algorithm a flow network is modelled as a broad band telecommunication network allowing mixed mode of information (i.e. audio, video and data etc.) to flow through it. For convenience a two commodity multistate flow network problem (TCMFN) is considered for illustration purpose i.e. the network allows to flow two commodities (audio files as commodity 1 and video files as commodity 2) concurrently share the bandwidth (capacity) of the network. |
PROBLEM FORMULATION
|
| A path is an ordered sequence of arcs and nodes connecting sto t. The paths whose proper subsets are no longer the path are called minimal path. The system reliability is the probability that the given demand (d1, d2) within the budget Bcan be transmitted through source to destination. Hence, the necessary conditions to be obeyed by the current capacity vector Xto be a (d1, d2, B) minimal flow path (i.e. (d1, d2, B)-MP) are1)the Xmust belong to a feasible set of flow |
 |
 |
 |
| A. Generating all (d1,d2,B) - MP |
| To generate all (d1,d2,B)- MP set a new continuous genetic algorithm based has been suggested. The development of GA can be termed as an adaptation of a probabilistic approach based on principles of natural evolution. Nature observes the principle of survival of fittest, weak and unfit species within their environment are faced with extinction by natural selection. The strong ones have greater opportunity to pass their genes to future generations via reproduction [20], [21]. The genetic algorithms follow the process in which populations undergo continuous change through cross breeding, mutation and natural selection. To generate all the (d1,d2,B)- MP (performance measure)and evaluate the Rd1, d2, B MP efficiently the objective function for the GA is formulated by considering X be a d1,d2,B)- MP implies that there exists a flow assignment (F1, F2) satisfying the demand constraints such as; |
 (9) (9) |
 |
| B. Proposed Genetic Algorithm |
| To evaluate all the d1, d2, B − MP a new continuous GA has been proposed in this section. Success of any GA depends onthe values of its parameters, such as; chromosome formation (i.e. coding technique), population size, crossover rate, mutation rate etc..The values of these parameters can be appropriately chosen to balance both the quality of the solution and the computational work. An initial population of a fix number of solutions is randomly generated to form the first generation population of the GA. Crossover and mutation operators are then performed on the population members to produce subsequent generations. An effective GA depends on complementary crossover and mutation operators. The crossover operator dictates the rate of convergence, while the mutation operator prevents the algorithm from prematurely converging. Each member of the population is evaluated in accordance with its objective function, which is used as basis for selecting parent solutions and also for culling inferior solutions to from the different evolution of population [25].In case of GA’s, if the values of the variables are continuous then it requires many bits to represent it. Further, if the number of variables is large, the size of the chromosome is also large. When the variables are naturally quantized, the binary GA fits nicely and the precision is limited to the binary representation of variables. However, when the variables are continuous, it is more logical to represent them by floating-point numbers. In addition, using floating point numbers allows chromosome representation to the machine precision and requires less storage than the binary GA. The continuous GA’s also have better inherent temporal efficiency because the chromosomes decoding prior to the evaluation of the objective function is not needed at all. |
| The reliability evaluation problem of a flow network under budget constraints when each node or arc has several possible capacities and may fail and the capacity weight varies with arc, nodes and types of commodity through the network is termed as a multiobjective optimization (MOO) of the stochastic flow network. In MOO there is usually no single solution that is optimum with respect to all objectives and consequent set of optimal solutions is known as Pareto optimal solutions. Without additional information, all these solutions are equally satisfactory. The goal of MOO is to find as many of these solutions as possible. If reallocation of resources cannot improve one cost without raising another cost, then the solution is Pareto optimal. The author [23] first introduced a multi-objective evolutionary algorithm called the vector-evaluated GA or VEGA. Later author [24] suggested using a nondominated sorting procedure coupled with a niching strategy called sharing. Sharing takes into account that individuals in the same niche must share the available resources. Later the work of [25] suggested that the multi-objective genetic algorithm (MOGA) can be implemented by finding all nondominated chromosomes of a population and give them a rank of one. These chromosomes are removed from the population. Next all the nondominated chromosomes of this smaller population are found and assigned a rank of two. This process continues until all the chromosomes are assigned a rank. |
| C. Steps of GA |
| A new continuous genetic search algorithm using a nondominant chromosome shorting based approach to optimize the stochastic flow network and to evaluate its reliability is proposed in the following section. |
| 1) Chromosome Representation: Chromosome representation is a crucial part of any genetic algorithm. There are several ways of representingchromosome for any given problem. Generally GA works with the binary encodings, but for many industrial problems binary string is not a natural coding. Hence various non-string techniques such as: real number coding for constrained optimization problems and integer coding for combinatorial problems have been used to establish the chromosome. For the nonlinear integer programming problems of the type given by (3) above, the continuous integer encoding as a vector representation is more efficient |
| 2) Generation of Initial Population: A fixed number of chromosomes are randomly generated to form an initial population. In a chromosome, a gene at any locus is randomly generated integer between the lower and upper limits defined for each subsystem. A population size of 2000 is taken for each of the test problem. |
| 3) Evaluating the Fitness of Chromosomes: The fitness of the chromosomes is calculated by using the objective function of (9). All the chromosomes satisfying the flow demand and constraints are arranged in descending order of their fitness and ascending order of the cost of transportation and are associated as rank 1 capacity vectors. A copy of these chromosomes is maintained as a pool of (d1,d2,B) - MP solutions. Rest all the solutions are ranked in terms of their ascending order of violation of flow constraints and cost starting from 2. The population thus obtained is considered as the first generation population. |
| 4) Genetic Operators: Two genetic operators Crossover and Mutation are the backbone of any GA. Using these two operators new off springs of the genes are created at each generation |
| • Crossover Operator: It provides a thorough search of regions of the sample space to produce good solutions. Rank based weighted random pairing technique is used to perform the crossover/ mating operation. The probabilities assigned to the chromosomes in the mating pool are inversely proportional to their rank. This approach do not depends on the nature of problem and determines the crossover probability from the rankn, of the chromosome. The rank probability pnis determined as |
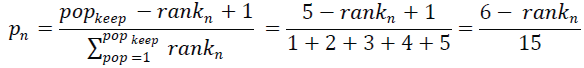 (14) (14) |
| popkeep represent the total number of chromosomes to be kept for next generation out of a given population in each iteration. If the rankn is the rank of the population and popkeep = 5 is the number of chromosome to keep then the cumulative probability assignment Σrank npop =1 ppop is show in Table 1. |
| The cumulative probabilities listed in column 4 are used in selecting the chromosome for mating purpose. A random number pis generatedbetween limits 0 ≤ p≤ 1 0. Starting from the top of the list, the first chromosome with a cumulative probability that is greater than or equal to the random number p is selected for the mating pool. For instance, if the random number is p= 0.437, then 0.333 <p ≤ 0.60, so chromosome2 is selected. The process is repeated to create the complete mating pool. Two-point crossover method is used to mate the parents and cut positionsare generated randomly from the interval [1, n]. |
| • Mutation: Random mutations alter a certain percentage of the bits in the list of chromosomes. Mutation is the other way to explore the search space exhaustively. The mutation ratepmis the ratethe rate at which new genes are introduced into the population for trial. If it is too low, then some genes that would have been useful are never tried out, but if it is too high, then there will be much random perturbation and the off springs will start losing their resemblance to the parents and the algorithm will lose the ability to learn from history. For the present GA,pmis taken as 0.20. Random number pis generated for each gene within the interval from interval 0 ≤p≤ 1. If p<pmthen the gene is randomly flipped to another gene from the corresponding set of alternatives. |
| 5) Selection: Each generation after undergoing genetic operations produces good or bad solutions. All the solutions (initial population, children and off springs) are arranged in descending order of fitness and the population is selected for the next generation. There after the steps (3) to (5)are iterated till either the stopping criteria is reached or maximum numbers of iteration are touched. |
ILLUSTRATION
|
| To illustrate the proposed, a benchmark problem used by [1] is considered. Figure 1 shows a bridge network consisting of 4 nodes and 6 arcs and multicommodity are to be transported through the flow network from s to t. Each route from s to t must pass through either node a7 or node a8. Considertwo commodities, one consisting of 150 data files of 100KB each (commodity 1) and other having 75 video files of 200KB each (commodity 2) have been considered for routing from s to t. The each route from s to t must pass through some intermediate nodes a7 and a8. All or any of the arc connecting source to terminal can fail, may be under maintenance or be occupied by some other transportation. Due to multiplicity of routes between source and terminal, the capacity of each arc is multistate. If at least two data packets of each commodity must be transported simultaneously (i.e. d1= 2 and d2 = 2) in the form of packets of 1000KB each through the network. It is evident that the commodity 1 consumes 15 packets (a wj1 = 1 1) and respectively commodity 2 consumes 30 packets (a wj1 = 1 1). Further the transportation has to be accomplished within a budget constraintC(X) ≤ B. The cost of transportation is bound to increase with the increase in number of containers. Thus, the objective of the flow networks is to maximise the flow and minimize the cost. The data of the example flow network of Fig. 1 is given in Table 2 with the objective to find the probability that system capacity is more or equal to demand (2, 2) under budget constraint B = 4400. The evaluation procedure of the problem is described in the following three Parts: |
 |
 |
 |
 |
CONCLUSIONS
|
| The proposed method is a GA based methodto evaluate the reliability of the stochastic flow network under budget constraints. It evaluates all the capacity vectors of the flow network satisfying the given flow and budget constraints using a new continuous GA based algorithm. The algorithm can easily be implemented by establishing the constraints (flow and budget etc.) inequalities in the algorithm without the knowledge of complicated mathematical inductions formulation. Hence, it can be easily implemented for determining the performance index of larger flow networks efficiently and find its utility in all modern transportation networks. |
Tables at a glance
|
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
|
Figures at a glance
|
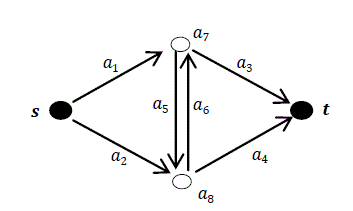 |
| Figure 1 |
|
References
|
- Y. K.Lin,“Reliability of a computer network in case capacity weight varying with arcs, nodes and types of commodity”, Reliability Engineering and System Safety, Vol. 2(5), pp. 1-7, 2006.
- Y. K. Lin, “Reliability of Flow Network subject to budget constraints”, IEEE Trans. Reliab., Vol. (56), pp. 10-16, 2007.
- Y. K. Lin, “System Reliability Evaluation for a Multistate Supply Chain Network with Failure Nodes Using Minimal Paths”, IEEE Trans.Reliab., Vol. 58(1), pp. 34-40, 2009.
- K. K. Aggarwal, Y. C. Chopra, and J. S. Bajwa, “Capacity consideration in reliability analysis of communication systems,” IEEE Trans.Rel., vol. 31, pp. 177-180, 1982.
- Y. K. Lin, “Reliability of kSeparate Minimal Paths Under Both Time and Budget Constraints”, IEEE Tran. On Reliab., Vol. 59(1), 183-190,2010.
- W. J. Rueger, “Reliability analysis of networks with capacity-constraints and failures at branches and nodes,” IEEE Trans. Rel., vol. 35, pp.523–528, 1986.
- D. W. Lee and B. J. Yum, “Determination of minimal upper paths for reliability analysis of planar flow networks,” Reliab. Eng. Syst. Saf.,vol. 39, pp. 1-10, 1993.
- J. Xue, “On multistate system analysis”, IEEE Trans Reliab., Vol. 34, pp. 329–37, 1985.
- W. C. Yeh, “A revised layered-network algorithm to search for all d-minpaths of a limited-flow acyclic network”, IEEE Trans. Reliab., Vol.47, pp.436–42, 1988.
- J. S. Lin, C. C. Jane and J. Yuan,“On reliability evaluation of a capacitatedflownetwork in terms of minimal pathsets”,Networks, Vol. 3,pp.131-138, 1995.
- Y. K. Lin,“A simple algorithm for reliability evaluation of astochastic-flow network with node failure”, Computer and Operation Research,Vol. 28(13), pp.1277-1285, 2001.
- W. C. Yeh,“A simple approach to search for all d-MCs of a limitedflownetwork”,Reliab. Engi. System Safety, Vol. 71(1), pp.15-19, 2001.
- Y. K. Lin,“Study on the multicommodity reliability of a capacitatedflownetwork”, Compu. Math.with Applications, 42(1-2), pp.255-264,2001.
- Y. K. Lin,“Using minimal cuts to evaluate the system reliability of astochastic-flow network with failures at nodes and arcs”, Reliab. Engi.System Safety, Vol. 75(1), pp.41-46, 2002.
- W.C. Yeh,“A simple algorithm to search for all d-MPs withunreliable nodes,” Reliab. Engi. System Safety, Vol. 73(1),pp.49-54, 2003.
- J. E. Cremeans, R. A. Smith, G. R.Tyndall, “Optimal multicommodity network flows with resource allocation”, Naval Res Logistics Q,Vol.17, pp. 269–279, 1970
- J. R. Evans, “A combinatorial equivalence between a class of multicommodity flow problems and the capacitated transportation problem”,Math Programming, Vol.10, pp. 401–404, 1976.
- L. R. Ford, D. R. Fulkerson, “A suggested computation for maximal multicommodity network flows”, Manage, Sci. Vol. 20, pp.822- 844,1974.
- A. A. Assad, “Multicommodity network flows-a survey”, Networks, Vol. 8, pp. 37-91,1978.
- P. Kumar, D. K. ChaturvediandG. L. Pahuja,“Constrained Reliability Redundancy Optimization of Complex Systems using GeneticAlgorithm”, MIT Int. J of Electrical and Instrumentation Engineering, Vol. 1, No. 1,pp. 41-48, 2011.
- P. Kumar, “Constrained Reliability Redundancy Optimization of Flow Networks using Genetic Algorithm”, Int. J. Adv. Res. Elec. , Electro.and Inst. Engineering, Vol. 2(5), pp. 1885-92, 2013.
- D. Coit, and A. Smith, “Reliability optimization of series-parallel systems using a genetic algorithm”, IEEE Trans. Reliab., Vol. 45(2), pp.254–60, 1996.
- J. D. Schaffer, et al., “A study of control parameters affecting online performance of genetic algorithms for function optimization”, in J.D.Schaffer (ed.), Proc. 3rd Int.Conf. on Genetic Algorithms. Los Altos, CA: Morgan Kaufmann, pp. 51–60, 1989..
- D. E. Goldberg, and J. Richardson, “Genetic algorithms with sharing for multimodal function optimization”, in J. J. Grefenstette (ed.),Genetic Algorithms and Their Applications: Proc. 2nd Int. Conf. on Genetic Algorithms, Hillsdale, NJ: Lawrence Erlbaum, pp. 41–49,1987.
- C. M. Foneseca, and P. J. Flemming, “Genetic algorithms for multi-objective optimization: Formulation, discussion, and generalization”,Proc. 5th Int. Conf. on Genetic Algorithms. San Francisco, CA: Morgan Kaufmann, pp. 416–423, 1993.
|