Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

A Hybrid Approach for Image Data Security

Aswathy Elma Aby
Lecturer, Dept. of ECE, College of Engineering, Kottarakara, Kerala, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Image data security plays an eminent role in personal identification. They are needed in different fields like banking, passport control etc. Suitable countermeasures are to be employed to make the enrolled data inaccessible to intruder,; unless security of the approach cannot be ensured. This work introduces a technique for providing template image data secure by using Visual Cryptography Scheme (VCS), Grey level Extended Visual Cryptography Scheme (GEVCS), Principal Component Analysis (PCA) and Euclidian distance approach. The results show that the reconstructed image as well as the share images are similar in appearance to the original target image and the host images respectively.

Keywords
Biometric database, Euclidian distance, GEVCS, PCA

INTRODUCTION
Biometrics refers to identifying human features for personal authentication. Multimodal biometric approaches are preferred over unimodal biometrics since the later has design limitations such as noise in input data, intra-class variation, interoperability, vulnerability against spoof attacks, inter-class similarities etc. To make the data inaccessible for imposter, some countermeasures are to be employed (e.g. encryption or anonymous techniques). Unless, storing biometric features in servers will not be secure.
For protecting privacy of biometric data enrolled in database, Davida et al. [1] and Ratha et al. [2] proposed a technique to store transformed biometric template in the database, instead of original biometric template. A three-step hybrid approach is proposed by Feng et al. [3] that combined the advantages of cancelable biometrics and cryptosystems. Other than these methods, researchers suggest various image hiding approaches [4]–[6] to provide anonymity to the stored biometric data. A face swapping technique which protects the identity of a face image by automatically substituting it with replacements taken from face images of a public dataset is proposed by Bitouk et al [7]. However, in case of face swapping and aggressive de-identification, there are chances of original face image to be lost.
Naor and Shamir [8] introduced a secure way to allow secret sharing of images without using cryptographic schemes and is called Visual Cryptography Scheme (VCS). In this scheme, encryption is performed such that decryption can be done by the human visual system. Later, Nakajima and Yamaguchi [9] presented a 2-out-of-2 extended VCS known as the gray-level extended visual cryptography scheme (GEVCS) for natural image encoding. Recently, Arun Ross and Asem Othman [10] explored the possibility of using GEVCS for imparting privacy to biometric face images using Active Appearance Model (AAM) [11].
A biometric data hiding technique which addresses template protection requirements such as diversity, revocability, security and better recovery performance along with reduced computational complexity and easier decryption is preferable. This work explores the possibility of using GEVCS along with PCA and Euclidean distance approach to satisfy these requirements. Privacy to biometric face image is ensured by decomposing original image into two images such that the original image can be recovered only if both images are simultaneously available. Also, any information about the original image cannot be revealed from individual component images. It provides successful matching of face images reconstructed from the sheets and also less cross-database matching for determining identities.
Biometric processing includes enrollment and authentication/identification. The private biometric data is sent to a trusted third party after enrollment. Once the trusted entity receives the data, the image is then decomposed into two images known as sheets. The decomposed components are then transmitted and stored in two different database servers. Thus it prevents revealing the identity of private data to either server. Upon the request of the trusted entity to each server, the corresponding sheets are transmitted to it during the authentication process. In order to reconstruct the private image, sheets are superimposed.
In case of face images, after decomposing each private image,they are encrypted into two different public host face images. While using non-face images as hosts, it results in visually revealing the existence of a secret face. Decomposing the face image into random noise structures may also pique the interest of an eavesdropper by suggesting the existence of secret data in it.
The rest of the paper is organized as follows. Section II gives an idea about the Visual Cryptographic technique, section III and IV explains the proposed approach for securing fingerprint templates and face images respectively. Section V shows the experimental results and section VI concludes the paper.

VISUAL CRYPTOGRAPHY
A. Visual Cryptography Scheme (VCS)
The visual cryptography scheme (VCS), proposed by Naor and Shamir [8] provides a simple and secure way to allow the secret sharing of images without any cryptographic algorithms. The basic scheme of VCS is referred as the k-outof- n VCS which is also denoted as (k, n) VCS [8] and it deals with binary images. In this scheme, the original binary image T is encrypted in ‘n’ images, such that
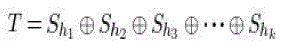equation (1)
where + is a Boolean operation, k ≤ n , ‘n’ is the number of noisy images, Shi; hi Є (1,2,…,k), is a share image, and it appear as white noise. Using individual Shi’s, it is difficult to decrypt the secret image T [8]. The encryption is done such that ‘k’ or more out of ‘n’ generated images are necessary to reconstruct the original private image T.
B. Gray-Level Extended Visual Cryptography Scheme (GEVCS)
In VCS, the sheets appear as a random set of pixels. They may generate curiosity of an interceptor by suggesting the existence of a secret image inside. To mitigate this problem, Naor and Shamir [8] suggested an approach to reformulate the sheets as natural images. Such a framework was introduced by Ateniese et al. [12] known as the extended VCS. A theoretical framework to apply extended visual cryptography on grayscale images (GEVCS) is proposed by Nakajima and Yamaguchi [9]. They also introduced a method to enhance the contrast of the target images in it. For GEVCS, the dynamic range of the original and host images are at first changed and then a Boolean operation is applied on the halftoned pixels of the two hosts and the original image.
During encryption, the sub pixel arrangement in the shares of both hosts has to be controlled to obtain required transparency (the number of white sub pixels) of target pixel. But there are cases when the required transparency for the corresponding pixel in the target image cannot be obtained, however the shared sub pixels are rearranged.
Nakajima and Yamaguchi [9] described a method to decrease the number of violated triplets by performing an adaptive dynamic range compression and thus enhance the image quality (contrast). The error generated while adjusting the gray levels of the conflicting triplets are diffused to nearby pixels. Thus to facilitate this adjustment, both halftoning and encryption are done simultaneously.

SECURING FINGERPRINT TEMPLATES
Visual cryptography is used for securing fingerprint templates. The superimposing operation in visual cryptography is computationally modelled as binary OR operation which causes the contrast level of target image to be lowered. Loss in contrast in target images could be addressed by substituting the OR operator with the XOR operator.
Furthermore, the target image can be down-sampled by reconstructing one pixel from every 2 x 2 block. Thus, the reconstructed image will be visually appealing with less storage space requirement.

SECURING FACE IMAGES
Let H be the desired private face image and R={P1, P2 … PN} the public dataset containing a set of host images. At first two host images Pi and Pj, i≠j where i,j =1,2…N are to be selected from R that can hide the private face image. Variations in face geometry and texture between the private face image and the images in the public dataset may result in perceptibility of the impact of the target image on the sheet images and vice versa. By carefully choosing host images for a particular private image, this issue can be mitigated. The steps for this approach will be explained in detail in the following subsections.
A. Principal component analysis (PCA)
Host images are to be selected such that they are most likely to be compatible with the private image. For this we here used principal component analysis with “Eigenface” [13] approach. To determine the similarity between private face image and candidate host images, the design of the face recognition system is based upon “eigenfaces”. By means of PCA the features of the original images of the training set are transformed into a set of eigenfaces E. For each image of the training set, the weights are calculated and are stored in a set W. Upon observing an unknown image Y, the weights for that particular image is calculated and stored in the vector WY. For host selection, WY is compared with the weights of images of W, the training set.
B. Selection of Hosts
Selection of hosts is done by Euclidean distance[14]. If A and B are two vectors of length D, the distance between them is determined as:
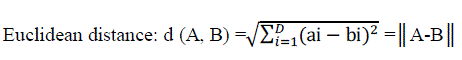equation (2)
The distances are then sorted in order to locate two suitable host images, HS1 and HS2.
C. Secret Encryption and Reconstruction
To encrypt the secret image H in the two host images PS1 and PS2, GEVCS is used. It generates two data encrypted sheet images denoted as S1 and S2, respectively. In order to reveal the secret private image, S1 and S2 are superimposed. To retain the original image size while reconstructing the final target image, pixel expansion step is reversed.

EXPERIMENTAL RESULTS
We used MATLAB simulation to evaluate the performance of proposed technique.Fig.1 shows a fingerprint and the corresponding shares generated from it by applying VCS. The share image provides no information about the original image.
In case of face images, we assigned a public dataset containing a set of candidate host images that can hide the assigned private face image. Fig.2 shows the assigned public dataset for host selection. For analysis, we took a dataset consisting of images of four persons each with three images.
The first task is to train the images of each person in the dataset to generate corresponding eigenface, and it is done using PCA. Fig. 3 and fig.4 shows an example of the dataset images of a person and the corresponding eigenface respectively.
Selection of two host images from the public dataset to encrypt the private face image is done by analyzing these eigenfaces. The images are selected such that, they are most likely to be compatible with the private face image. Face images that have minimum Euclidian distance with the private face image are selected as host images. Fig.5 shows the process of host selection.
The private face is then encrypted in selected host images. It is then halftoned and stored in two different database servers. The halftoned private face image which is then encrypted in host images is shown in fig.6. The reverse process is performed during the decryption. Fig.7 shows the encrypted share images stored in database and the recovered private face from them.
The reconstructed image as well as the share images is similar in appearance to the original target image and the host images respectively. Thus it prevents the intruders not to have any idea of the existence of a secret face image in the share images.

CONCLUSION
This work explored the possibility of using VCS, GEVCS and PCA for imparting privacy to biometric templates. To protect the privacy of a face image in the database, the input private face image is decomposed and encrypted in two independent host images. The private face image can be reconstructed only when both sheets are simultaneously available. It is able to obtain the reconstructed images from sheet images similar to original private image. Also it is computationally hard to obtain the private biometric image from the individual stored sheets due to visual cryptography, which enhance the system security.

Figures at a glance


Figure Figure Figure Figure
Figure 1 Figure 2 Figure 3 Figure 4
Figure Figure Figure
Figure 5 Figure 6 Figure 7

References