A Hybrid approach for PNN-Based MRI
Brain Tumor Classification and Patient
Detail Authentication Using Separable
Reversible Hiding

Ms.K.Kothavari; R.Keerthana; M.Mariselvam; S.Kaveya; L.Mekala

A Hybrid approach for PNN-Based MRI Brain Tumor Classification and Patient Detail Authentication Using Separable Reversible Hiding

Ms.K.Kothavari¹, R.Keerthana², M.Mariselvam²,S.Kaveya² and L.Mekala²

Associate Professor, Department of ECE, Dr.N.G.P. Institute of Technology, Coimbatore, TamilNadu, India
U.G.Student, Department of ECE, Dr.N.G.P. Institute of Technology, Coimbatore, TamilNadu, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The objective of this study is to employ Probabilistic Neural Network with MRI image and data processing techniques to implement an automated brain tumor classification and to propose a novel scheme for separable reversible data hiding in encrypted MRI images. Medical Resonance images (MRI) contain a noise caused by operator performance which can lead to serious inaccuracies in classification. The use of artificial intelligent techniques for instant, neural networks, and fuzzy logic show great potential in this field. Hence, in the classification process, Probabilistic Neural Network is applied. Decision making is performed in two stages: feature extraction using the principal component analysis and the Probabilistic Neural Network (PNN).In authentication phase, the medical practitioners can encrypt the original uncompressed image using an encryption key. Then, data-hiding is performed by compressing the least significant bits of the encrypted image to create a sparse space to accommodate patient information. If the receiver has the encryption key, the additional data and the original content can be encrypted and recovered without any error by exploiting the spatial correlation in natural image. Probabilistic Neural Network gives fast and accurate classification and isa promising tool for classification of the tumors and separable reverse hiding technique is an entrusted technique for information authentication.

Keywords

PNN, Neural Network, PCA, MRI, Classification, Image Encryption, Reversible Data Hiding.

INTRODUCTION

Brain tumors are considered as one of the most lethal and difficult to identify and to be treated forms of cancer. Although the WHO grading scheme provides accurate definitions for tumor grade determination, every pathologist gives different relative importance to each of the grading criteria. Thus, there is significantly promoting inter and intra observer variability that has been shown to significantly influence the quality of diagnosis. Computer based techniques, have been extensively examined for improving grade diagnosis and until today remains an active research area. But even in automated systems, pre-processing and classification with less computational time with increased efficiency is being a major drawback..The purpose of artificial intelligence technique is to implement an automated brain tumor classification with increased accuracy and speed. This is performed in three stages: pre-processing for removal of impulse noise and image enhancement, feature extraction for image recognition and compression and pattern classification for classification of tumors. Reversible data hiding is a technique which enables images and personal details of patients to be authenticated and then restored to their original form by giving a secret key. This would make the images acceptable for legal purposes.

PRE- PROCESSING

MR images are generated by a complex interaction between static and dynamic electromagnetic fields and the tissue of interest, namely the brain that is encapsulated in the head of the subject. Hence, the raw images contain noise from various sources -- namely head movements that can hardly be corrected or modeled, and bias fields. So to avoid those noises, pre- processing is necessary. Pre- processing includes removal of noise and image enhancement. Several filters have been implemented to reduce impulse noise.

A. Removal of Noise

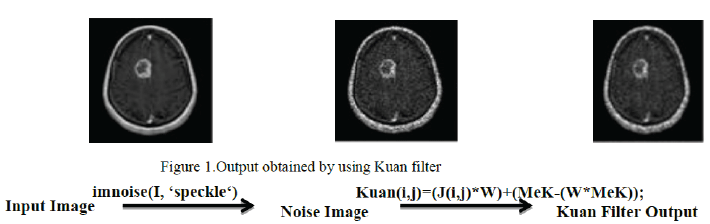
For removal of impulse noise, the filter which have been implemented in Kuan filter,Kuan filter smoothens the image without removing edges or sharp features in the images. Kuan filter first transforms the multiplicative noise model into a signal-dependent additive noise model. Then the minimum mean square error criterion is applied to the model. Because Kuan filter made no approximation to the original model, it can be considered to be superior to the Lee filter. The resulting grey-level value R for the smoothed pixel is:

R=I_c*W +I_m* (1−W) where,

I_c= centre pixel in filter window,I_m = mean value of intensity within window and W=weighting factor ,the output of kuan filter is shown in figure 1

B .Image Enhancement

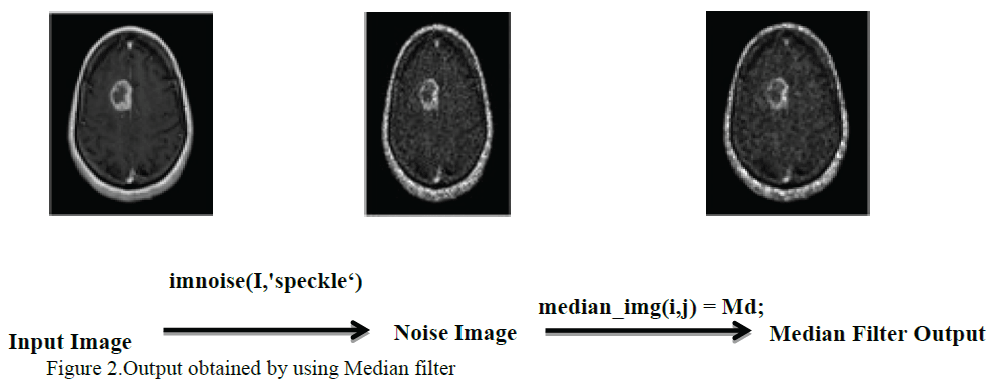
Image enhancement refers to accentuation, sharpening of image features such as boundaries, or contrast to make a graphic display more useful for display & analysis. It includes grey level & contrast manipulation, noise reduction, edge crisping and sharpening, filtering, interpolation and magnification and pseudo coloring. The enhancement filters used for better interpretation of the image is Median Filter.

A median filter is a non-linear filter and is efficient in enhancing the image. Median preserves the sharpness of Image edges while removing noise. It can effectively remove speckle noise at the expense of blurring of edges.The output obtained by using median filter is given in figure.2.

Table 1 illustrates the comparison of denosing filters and Table 2 illustrates comparison of enhancement filters

FEATURE EXTRACTION USING PRINCIPAL COMPONENT ANALYSIS (PCA)

The principal component analysis (PCA) is used as a feature extraction algorithm. The principal component analysis (PCA) is one of the most successful techniques that have been used in image recognition and compression. The purpose of PCA is to reduce the large dimensionality of the data.

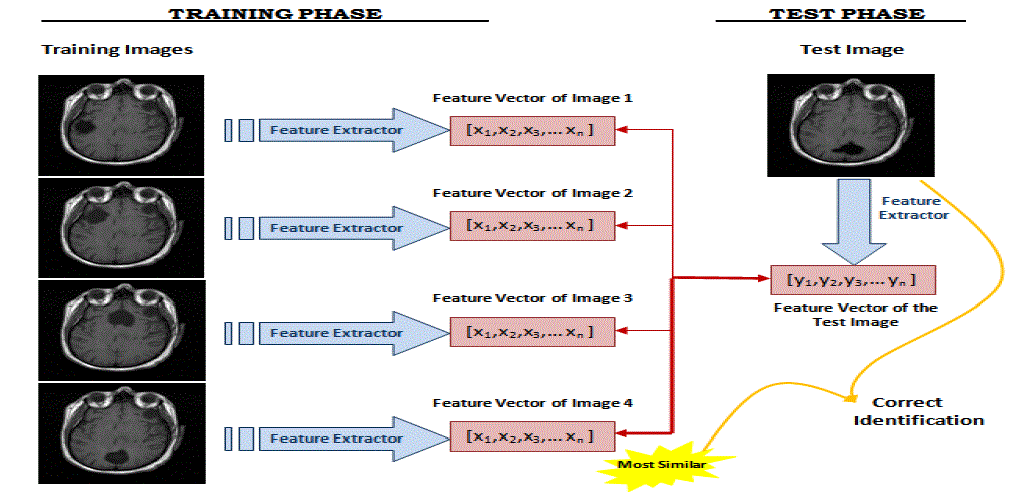
Phases of Principal Component Analysis: It has two phases namely the training phase and the test phase.MR image recognition systems find the identity of a given test image according to their memory. The task of an image recognizer is to find the most similar feature vector of a given test image.In the training phase, feature vectors are extracted for each image in the training set. Let Ω1 be a training image of image 1 which has a pixel resolution of M x N (M rows, N columns). In order to extract PCA features of Ω1, first image is converted into a pixel vector Φ1 by concatenating each of the M rows into a single vector. The length (or, dimensionality) of the vector Φ1 will be M x N. Here, the PCA algorithm is used as a dimensionality reduction technique which transforms the vector Φ1 to a vector ω1 which has a dimensionality d where d << M x N. For each training image Ωi, these feature vectors ωi are calculated and stored.In the testing phase, the feature vector ωj of the test image Ωj is computed using PCA. In order to identify the test image Ωj, the similarities between ωj and all of the feature vectors ωi’s in the training set are computed. The similarity between feature vectors is computed using Euclidean distance. The identity of the most similar ωi is the output of the image recognizer. If i = j, it means that the MR image j has correctly identified, otherwise if i ≠ j, it means that the MR image j has misclassified.

Schematic diagram of the MR image recognition system that is implemented is shown in figure.3

PROBABILISTIC NEURAL NETWORK

The probabilistic neural network was developed by Donald Specht. This network provides a general solution to pattern classification problems by following an approach developed in statistics, called Bayesian classifiers Probabilistic Neural Network gives fast and accurate classification and is a promising tool for classification of the tumors. Existing weights will never be alternated but only new vectors are inserted into weight matrices when training. So it can be used in real-time. Since the training and running procedure can be implemented by matrix manipulation, the speed of PNN is very fast.

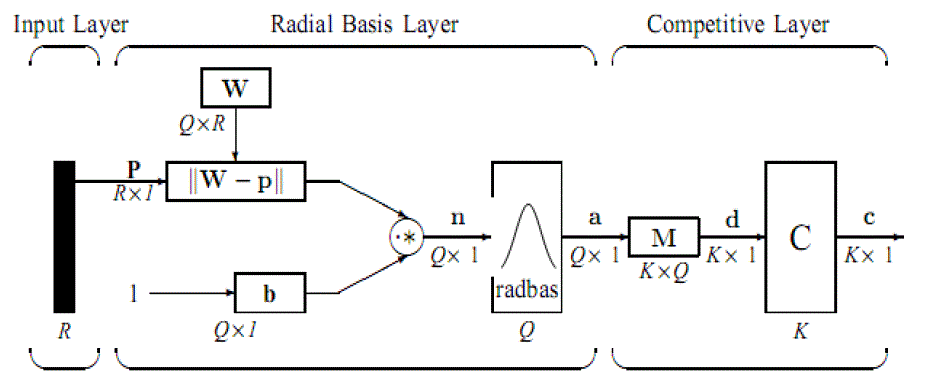
Structure of Probabilistic Neural Network:The network classifies input vector into a specific class because that class has the maximum probability to be correct. The PNN has three layers: the Input layer, Radial Basis Layer and the Competitive Layer. Radial Basis Layer evaluates vector distances between input vector and row weight vectors in weight matrix. These distances are scaled by Radial Basis Function nonlinearly. Then the Competitive Layer finds the shortest distance among them, and thus finds the training pattern closest to the input pattern based on their distance. The network structure is illustrated in figure.4

1) Input Layer: The input vector, denoted as p, is presented as the black vertical bar in Fig. 4.9. Its dimension is R × 1.

2) Radial Basis Layer: In Radial Basis Layer, the vector distances between input vector p and the weight vector made of each row of weight matrix W are calculated. Here, the vector distance is defined as the dot product between two vectors. Assume the dimension of W is Q×R. The dot product between p and the i-th row of W produces the i-th element of the distance vector ||W−p||, whose dimension is Q×1, as shown in Figure. 4.9. The minus symbol, “−”, indicates that it is the distance between vectors. Then, the bias vector b is combined with ||W− p|| by an element-by element multiplication, represented as “.*” in Figure. 5. The result is denoted as n = ||W− p|| .*p.The transfer function in PNN has built into a distance criterion with respect to a center. It is defined as

radbas(n) =e−n2 ………………………………………………………………………………………(1)

Each element of n is substituted into Eq. 1 and produces corresponding element of a, the output vector of Radial Basis Layer. The i-th element of a can be represented as

a_i = radbas(||W_i− p|| .*b_i)…………………………………………………………………………….. (2)

where W_i is the vector made of the i-th row of W and b_i is the i-th element of bias vector b.

3) Some characteristics of Radial Basis Layer: The i-th element of a equals to 1 if the input p is identical to the ith row of input weight matrix W. A radial basis neuron with a weight vector close to the input vector p produces a value near 1 and then its output weights in the competitivelayer will pass their values to the competitive function. It is also possible that several elements of aare close to 1since the input pattern is close to several training patterns.

4) Competitive Layer: There is no bias in Competitive Layer. In Competitive Layer, the vector a is firstly multiplied with layer weight matrix M, producing an output vector d. The competitive vector of competitive function is denoted as c. The index of 1 in c is the number of tumor that the system can classify.

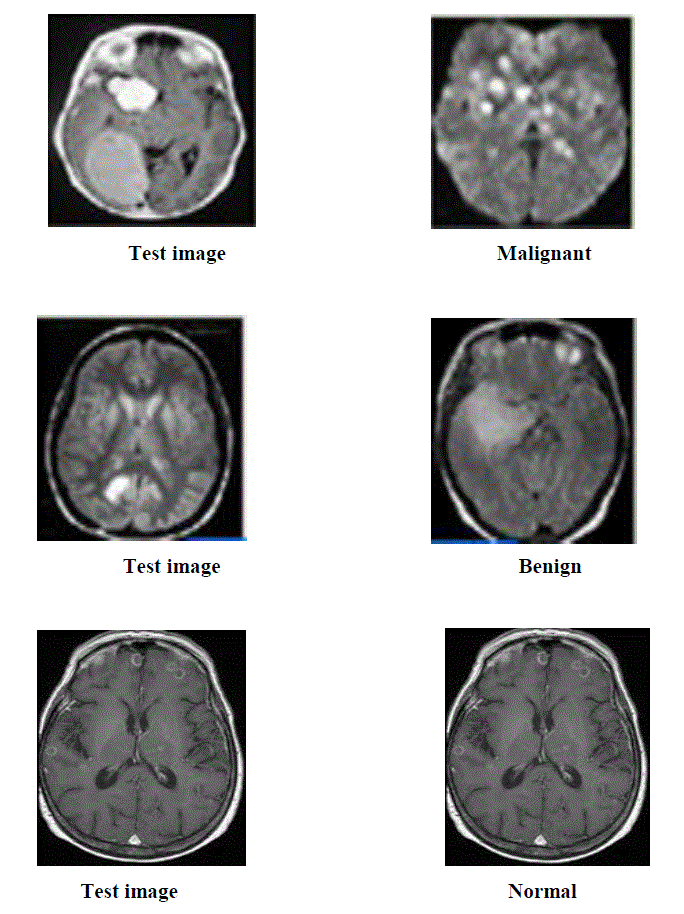
The output for classification of brain tumors asmalignant, beningn and normal using Probabilistic Neural Network is given in figure.5

SEPARABLE REVERSIBLE DATA HIDING IN ENCRYPTED IMAGES

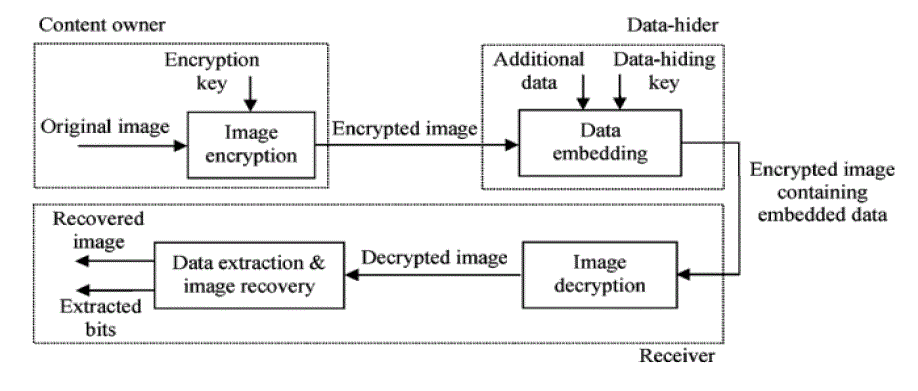
Separable Reversible data hiding is a technique which enables images to be authenticated and then restored to their original form by removing the digital watermark and replacing the image data that had been overwritten to their original form by removing the digital watermark and replacing the image data that had been overwritten. The steps involved in separable reversible data hiding in encrypted images are Image Encryption, Data Embedding, Image Decryption, Data Extraction and Image Recovery.

The schematic diagram of separable reversible data hiding is given in figure 6.

A. Image Encryption

Image encryption is the process of encoding the pixels of the image in such a way that eavesdroppers or hackers cannot read it, but that authorized parties can. In an encryption scheme, the cover image is encrypted using an encryption algorithm, turning it into an unreadablestego image. This is usually done with the use of an encryption key, which specifies how the message is to be encoded. An authorized party, however, is able to decode the stego image using a decryption algorithm, that usually requires a secret decryption key,that adversaries do not have access to. For technical reasons, an encryption scheme usually needs a key-generation algorithm to randomly produce keys. This is done by assuming each pixel with gray value of the original image falling into [0, 255] represented by 8 bits and denoting the gray value as p i,j ,where ( i , j) indicates the pixel position, and bits of a pixel as b i,j,0 , b i,j,1 ,…, bi,j,7for k=0,1,2

B. Data Embedding

In the data embedding phase, some parameters are embedded into a small number of encrypted pixels, and the LSB of the other encrypted pixels are compressed to create a space for accommodating the additional data and the original data at the positions occupied by the parameters. It is done bysegmenting the encrypted image into non-overlapping blocks sized by s × swhere Bi,j,k should satisfy

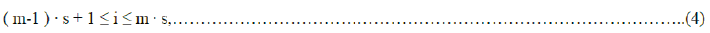C. Image Decryption

Image Decryption is simply the reverse of encryption, the process by which ordinary data, or stego image, is converted into the original cover image. With an encrypted image containing additional data, a receiver may first decrypt it according, and then extract the embedded data and recover the original image by using the encryption key. At the receiver side, the data embedded in the created space can be easily retrieved from the encrypted image containing additional data according to the encryption key. Since the data embedding only affects the LSB, a decryption with the encryption key can result in an image similar to the original version.

D. Data Extraction

E. Image Recovery

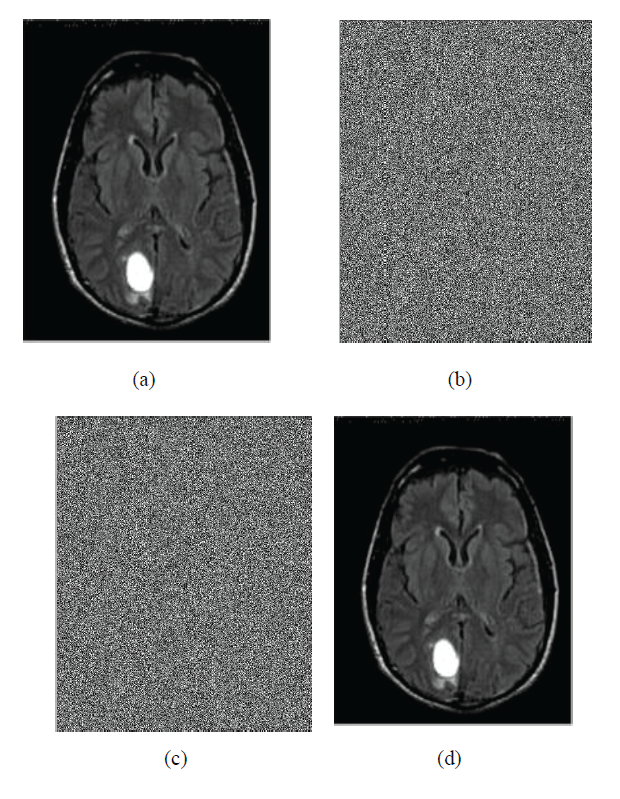
If f0< f1 ,H0 is the original content ,the extracted bit be 0. If f0> f1,H1 is the original content , the extracted bit be 1. The extracted bits are concatenated and the recovered blocks are collected.The output for seperable reversible data hiding is given in figur7.The figure7(a) is the original image, figure.7(b) is the image obtained as a result of encryption, figure7(c) represents the encrypted image containing embedded data and the figure7(d) gives the directly decrypted image which is the original image.

CONCLUSION

In this paper, PNN has been implemented for classification of MR brain image. PNN is adopted for it has fast speed on training and simple structure. Twenty images of MR brain were used to train the PNN classifier and tests were run on different set of images to examine classifier accuracy. The developed classifier was examined under different spread values as a smoothing factor. Experimental result indicates that PNN classifier is workable with an accuracy ranged from 100% to 85% according to the spread value[5]. Separable Reversible Data Hiding in Encrypted images after classification of brain tumor is implemented for the purpose of authentication and integrity. In authentication phase, the medical practitioners can encrypt the original uncompressed image using an encryption key. Then, data-hiding is performed by compressing the least significant bits of the encrypted image to create a sparse space to accommodate patient information. If the receiver has the encryption key, the additional data and the original content can be encrypted and recovered without any error by exploiting the spatial correlation in natural image[1].

Tables at a glance


Table 1	Table 2

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4

Figure 5	Figure 6	Figure 7

References

Xinpeng Zhang , ”Separable Reversible Data Hiding in Encrypted Image”, ieee transactions on information forensics and security, vol. 7,no. 2, April 2012.

Booma Devi Sekar, Ming Chui Dong, Jun Shi, and Xiang Yang Hu, “Fused Hierarchical Neural Networks for Cardiovascular DiseaseDiagnosis”, ieee sensors journal, vol. 12, no. 3, March 2012.

P. Georgiadis et al, “Quantitative combination of volumetric MR imaging and MR spectroscopy data for the discrimination ofmeningiomas from metastatic brain tumors by means of pattern recognition”, magnetic resonance imaging 29 525–535, Elsevier B.V, 2011.

Nikola K. Kasabov, Fellow, IEEE, ReinhardSchliebs, and Hiroshi Kojima, “Probabilistic Computational Neurogenetic Modeling:From Cognitive Systems to Alzheimer’s Disease”,ieee transactions on autonomous mental development, vol. 3, no. 4, December 2011.

MohdFauzi Othman and MohdAriffananMohdBasri, “ Probabilistic Neural Network for Brain Tumor Classification”, second internationalconference on intelligent systems, modeling and simulation, 2011

T. Bianchi, A. Piva, and M. Barni, “Composite signal representation forfast and storage-efficient processing of encrypted signals,” IEEETrans.Inform. Forensics Security, vol. 5, no. 1, pp. 180–187, Feb. 2010.

7 W. Liu, W. Zeng, L. Dong, and Q. Yao, “Efficient compression of encryptedgrayscale images,” IEEE Trans. Image Process., vol. 19, no.4,pp. 1097–1102, Apr. 2010.

Mrs.MamataS.Kalas, “ An Artificial Neural Network for Detection of Biological Early Brain Cancer”, international journal of computerapplications(0975 – 8887) vol. 1 – no. 6, Elsevier B.V, 2010.

Jian-Bo Yang, Kai-QuanShen, Chong-Jin Ong, and Xiao-Ping Li, “Feature Selection for MLP Neural Network: The Use of RandomPermutation of Probabilistic Outputs”, ieee transactions on neural networks, vol. 20, no. 12, December 2009.

Fe´ lix F.Gonza´ lez-Navarro, “ Feature and model selection with discriminatory visualization for diagnostic classification of braintumors” , Elsevier B.V, 2009.

E.I. Papageorgiou, “ Brain tumor characterization using the soft computing technique of fuzzy cognitive maps”, Elsevier B.V, 2009