Keywords
|
| Hybrid particle swarm optimization (HPSO), optimal power flow, cost minimization, two step initialization, power systems. |
INTRODUCTION
|
| Optimal power flow plays an important role in power system operation. It simply attempts to find the optimal settings of a given power system network that optimize a certain objective function while satisfying its power flow equations, system security and equipment operating limits. Several control actions, some of which are generator’s real power outputs and voltages, transformer tap changing settings, phase shifters, switched capacitors and reactors, are adjusted to achieve an optimal network setting based on the problem formulation. One of the main difficulties of the OPF problem is the nature of the control variables since some of them are continuous (real power outputs and voltages) and others are discrete (transformer tap setting, phase shifters and reactive injections). The overall fuel cost function is by far the most common objective used in OPF studies. However, other traditional objectives are minimization of active power loss, bus voltage deviation, emission of generating units, number of control actions and load shedding. |
| In the past conventional methods were employed for the solution of OPF problem. H.W.Dommel and W.F.Tinney [1] firstly presented the solution of optimal power flow.Various non-classical optimization tools have emerged to cope with some of the traditional optimization algorithms. The main modern optimization techniques are Genetic Algorithm (GA) [2-4], Evolutionary Programming (EP) [5], Artificial Neural Network (ANN), Simulated Annealing (SA), Ant Colony Optimization (ACO), Particle Swarm Optimization (PSO) [6] and Intelligent Search Evolutionary Algorithm (ISEA) [7]. Most of these relatively new developed tools mimic a certain natural phenomenon in its search for an optimal solution like species evolution (GA and EP), human neural system (ANN), thermal dynamics of a metal cooling process(SA), or social behaviour (ACO and PSO). They have been successfully applied to wide range of optimization problems in which global solutions are more preferred than local ones. |
| PSO has been previously used to solve the OPF problem. Researchers in references [8-10] have attempted to utilize PSO to solve the OPF problem considering different objective functions. In the aforementioned work, only continuous control settings were considered as optimization variables which restrict its applicability to real power systems. M.R.Al Rashidi and M.E.EI.Hawary [11] has reported a hybrid particle swarm optimization algorithm as a modern optimization tool to solve the discrete optimal power flow problem with valve loading effect. |
| In this paper, a HPSO algorithm capable of handling both discrete and continuous optimization variables is used to solve the OPF problem. The OPF problem was formulated as an optimization problem and solved using HPSO algorithm. The objective function is to minimize the fuel cost. A load flow model is used by incorporating Newton- Raphson iterative technique within the HPSO algorithm to minimize the total fuel cost. This model is further modified to incorporate TCSC [12-15] into the network and HPSO technique is applied to the model to enhance the performance of the power system. The effectiveness of the method was tested on standard IEEE 14 bus test system and the results are presented. |
THYRISTOR CONTROLLED SERIES CAPACITOR
|
| Series capacitive compensation was introduced decades ago to cancel a portion of the reactive line impedance and thereby increase compensation is highly effective in both controlling power flow in the lines and in improving stability. Thyristor Controlled Series Compensator (TCSC) is one of the important members of FACTS family that is increasingly applied with long transmission lines by the utilities in modern power systems. |
| The basic thyristor controlled series capacitor proposed in 1986 by Vithayathil with others as a method of “rapid adjustment of network impedance”. It consists of the series compensating capacitor shunted by a thyristor controlled reactor. In a practical TCSC implementation, several such basic compensators may be connected in series to obtain the desired voltage rating and operating characteristics. The basic idea behind the TCSC scheme is to provide a continuously variable capacitor by means of partially cancelling the effective compensating capacitance by the TCR. The basic scheme of TCSC is shown in Fig. 1 |
| TCSC is a device consisting of capacitor and thyristor controlled reactor (TCR) connected in parallel. This TCSC is one of FACTS equipment, which are used for active power flow control in electric power systems and to increase the transmission lines capability. The change of impedance of TCSC is performed by thyristor switched reactor connected in parallel to capacitor. Inductive reactance is defined by firing angle of thyristors. TCSC usually connects in series with line and allows changing impedance of transmission line and by this change to influence power flows. Control is fast, efficient and increase limits of transmitted power. |
MATHEMATICAL PROBLEM FORMULATION OF OPF WITH TCSC
|
| Mathematically, the OPF problem with FACTS to minimize fuel cost generation is solved by maintaining thermal and voltage constraints can be formulated as follows |
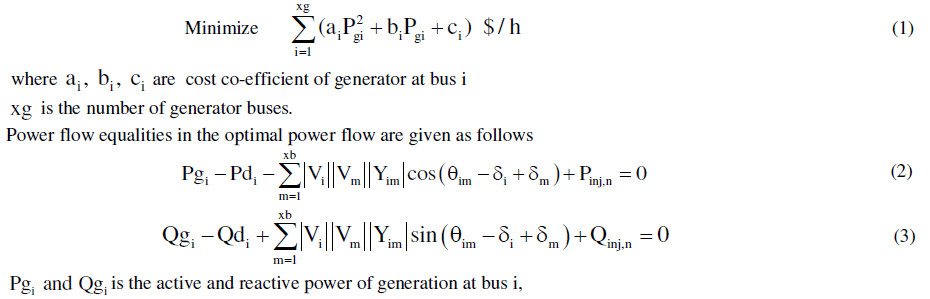 |
 |
HYBRID PARTICLE SWARM OPTIMIZATION
|
| A. Overview |
| Hybrid particle swarm optimization is a heuristic global optimization method put forward originally by Kennedy and Eberhart in 1995. It is developed from swarm intelligence and is based on the research of bird and fish flock movement behaviour. The original PSO model was intended to handle only continuous nonlinear optimization problems. However, further improvement elevated the PSO capabilities to solve a wider class of problems. The concept behind this optimizer came from early attempts conducted by Eberhart and Kennedy to model the flocking behavior of many species, like birds or school of fish in their food hunting. A swarm consists of number of particles that evolve or fly throughout the problem hyperspace to search for optimal or near optimal solution. |
| In N-dimensional search space, Xi = [xi1 ,xi2 , . . . xiN ] and vi = [vi1 ,vi2 , . . . viN ] are the two vectors associated with each particle i which indicates the initial position and velocity. During their search, particles interact with each other in a certain way to optimize their search experience. Throughout their flying experience, the particle with the best solution shares its position coordinates information with the rest of the swarm. Then, each particle updates its coordinates based on its own best search experience (pbest) and gbest. |
| This HPSO approach combines PSO technique with two step initialization approach in which the former technique is used as a global optimizer to find the best combinations of the mixed type control variables while the latter serves as a solver to the nonlinear power flow equations with better convergence characteristics. The HPSO employs a population of particles or possible solutions to explore the feasible solution hyperspace in its search for an optimal solution. Each particle’s position is used as a feasible initial guess for the power flow subroutine. This method of multiple initial solutions can provide better chance of detecting an optimal solution to the power flow equations that would globally minimize the objective function. |
| Similar to other evolutionary methods HPSO also starts with an initial population. Application of this algorithm to some benchmark functions and a real problem has proven its capability in solving complex, nonlinear and nonconvex optimization problems. The key features of the HPSO are faster convergence rate reduction in computational complexity. |
| B. HPSO algorithm |
| The major stages of the HPSO algorithm are briefly described as follows |
| • Initialization. |
| Two step initialization is used for generating initial population |
 |
| In this article, a two step initialization process is adopted. The two step initialization process provides better probability of detecting an optimal solution to the power flow equations that would globally minimize a given objective function. In the first step, initial population is generated as a multi-dimensional vector of size (ps × ncv) and it is considered as a village. All the control variables in the village must satisfy the constraints. Evaluate the value of cost function for each string in the village. Select the best string from the village corresponding to minimum cost. Repeat the procedure for number of villages (nv). In the second step, combine all the best strings from each village to form multi-dimensional vector [X] of size (nv ×ncv) and this new population is used for evolutionary operations. |
| • Weight updating |
| The weight is updated by using the following equation |
 |
| where |
| w is the inertia weight and it is a linearly decreasing function of the iteration index. |
| k is the iteration index. |
| • Velocity updating |
| By using the individual best and global best of the each particle. The jth particle velocity in the kth dimension is updated |
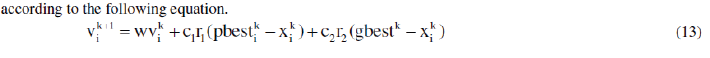 |
| where |
| c1 and c2 are two positive constants, they keep balance between the particle’s individual and social behaviours. |
| r1 and r2 are two randomly generated numbers with a range of [0,1] added in the model to introduce stochastic nature. |
| • Position updating |
| Based on the updated velocities, each particle changes its position according to the following equation. |
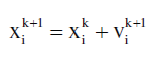 (14) (14) |
| • Selection |
| The population with best profit values are selected. Memorize the best solution achieved so far. |
| • Stopping criteria |
| Individual best population and global best population are copied to next generations until stopping criteria is satisfied. |
| In the current work, when the number of generations reaches the given maximum number of generations is used as stopping criterion. |
RESULTS AND DISCUSSIONS
|
| This paper has presented an OPF model incorporating FACTS controller which is TCSC using the HPSO algorithm for enhancement of system performance. This model is able to solve power networks of any size and converges with minimum number of iterations and independent of initial conditions. The standard IEEE 14-bus system has been used to demonstrate the proposed method over a wide range of power flow variations in the transmission system. |
| Simulation studies are carried out in this section to investigate the effects of the TCSC on the power system. The method is implemented using MATLAB software package on a personal computer with Intel Pentium dual core 2.6 GHz processor and 2 GB RAM. The HPSO algorithm is employed to solve OPF problem by incorporating TCSC for enhancement of system performance. The HPSO parameters used for the simulation are summarized in Table.1 |
| The network and load data for this system is taken from [16]. To test the ability of the HPSO algorithm one objective function is considered that is minimization of cost of generation. In order to show the effect of power flow control capability of the TCSC in HPSO algorithm, two case studies are carried out on the standard IEEE 14-bus system. |
| Case 1: OPF without TCSC |
| Case 2: OPF with TCSC. |
| From the Table 2 and Table 3, it can be seen that the installation of TCSC in the network gives the good performance of the system in terms of reduction in cost of generation, power loss reduction and better voltages. It also gives that HPSO algorithm is able to enhance the system performance while maintaining all control variables and reactive power outputs within their limits. |
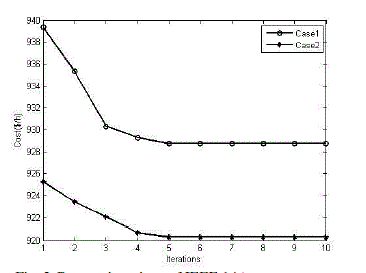
| The convergence characteristics with and without TCSC by using HPSO algorithm is shown in Fig.2. From the characteristics it can be seen that the convergence tendency is better with TCSC compared to without TCSC. |
CONCLUSIONS
|
| This paper incorporates the TCSC in OPF problem to minimize the fuel cost of generation and enhance the system performance. The HPSO algorithm is used for solving the OPF problem. The OPF problem is formulated as a nonlinear optimization problem with equality and inequality constraints. The results of the HPSO algorithm were compared with and without TCSC. Among the two test cases, test case 2 had the less fuel cost of generation, power loss reduction as well as voltage improvements. The convergence tendency of the HPSO algorithm shows that the algorithm relatively converges in less number of cycles. |
Tables at a glance
|
|
|
Figures at a glance
|
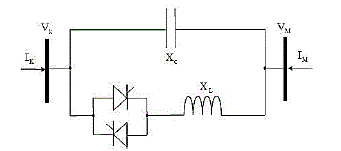 |
 |
| Figure 1 |
Figure 2 |
|
References
|
- H.W.Dommel and W.F.Tinney, “Optimal power flow solutions,” IEEE Transactions on power apparatus and systems, Vol.PAS-87, pp.1866-1876, Oct.1968.
- M. Melanie, “An introduction to genetic algorithms,” MIT Press, Massachusetts,1999.
- S.N. Sivanandam and S.N. Deepa, “Introduction to genetic algorithms,” Springer-Verlag, Berlin, Heidelberg, 2008.
- R.L. Haupt, S.E. Haupt, “Practical genetic algorithms,” seconded., John Wiley & Sons, New Jersey, 2004.
- R.Gnanadass, P.Venkatesh and Narayana Prasad Padhy, “Evolutionary programming based optimal power flow for units with non-smooth fuelcost functions,” Electric Power Components and Systems, Vol.33, pp.349-361, 2005.
- J. Kennedy and R. C. Eberhart, “Particle swarm optimization,” in Proc. IEEE Int. Conf. Neural Netw., Perth, Australia, Vol. 4, pp.1942–1948,1995.
- A.V.NareshBabu and S.Sivanagaraju, “A solution to the optimal power flow problem: A new approach based on two step initialization,” Proc.of IEEE India International Conference (INDICON) on Engineering Sustainable Solutions, BITS, Hyderabad, India, Dec. 2011.
- C. Wang, H. Yuan, Z. Huang, J. Zhang, and C. Sun, "A modified particle swarm optimization algorithm and its application in optimal powerflow problem," Proceedings of International Conference on Machine Learning and Cybernetics., vol. 5, pp. 2885-2889, Guangzhou, China,2005.
- R. Ma, P. Wang, H. Yang, and G. Hu, "Environmental/Economic Transaction Planning Using Multiobjective Particle Swarm Optimizationand Non-Stationary Multi-Stage Assignment Penalty Function," IEEE/PES Transmission and Distribution Conference and Exhibition: Asiaand Pacific, pp. 1-6, Dalian, China, 2005.
- B. Zhao, C. X. Guo, and Y. J. Cao, "Improved particle swarm optimization algorithm for OPF problems," IEEE/PES Power SystemsConference and Exposition, pp. 233-238, New York, USA, 2004.
- M.R.AI-Rashidi and M.E.EI-Hawary, “Hybrid particle swarm optimization approach for solving the discrete OPF problem considering thevalve loading effects,” IEEE Trans. Power Syst.,Vol.22, No.4, Nov.2007.
- N. G. Hingorani and L. Gyugyi, “Understanding FACTS-concepts and technology of flexible AC transmission systems,” IEEE press, FirstIndian Edition, 2001.
- Ghawghawe a ND, Thakre KL. Computation of TCSC reactance and suggesting criterion of its location for ATC improvement. Int J ElectrPower Energy Systems pp.86–93, 2009.
- Kazemi A, Badrzadeh B. “Modeling and simulation of SVC and TCSC to study their limits on maximum loadability point,” Int J ElectricPower Energy Syst. pp.381-8, 2004
- Canizares CA, Faur Z. “Analysis of SVC and TCSC controllers in voltage collapse,” IEEE Trans Power Systems, Vol.14, pp.1–8, 1999.
- IEEE 14-bus system data available at http://www.ee.washington.edu/research/pstca
|