Business Administration Department, Universidad Nacional del Sur San Andrés 800, Bahía Blanca, 8000, Argentina
Received: 13/08/2015 Accepted: 08/09/2015 Published: 18/09/2015
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
The main objective of this article is to analyze the average internal rate of return (AIRR) and the standard average internal rate of return (SAIRR) metrics on ambiguity contexts where fuzzy logic prevails. Either AIRR or SAIRR are employed improving the traditional IRR problems while determining cash flow returns. Having this in mind, we analyze, through a didactic hypothetical case, different AIRR aspects: its consistency in setting in order mutually exclusive projects of different size or scale; it congruency with the expected rate or the expected cash flow rate; and its versatility to adapt itself to fuzzy logic while keeping its coherence with net present value in setting in order alternatives.
Average internal rate of return, Fuzzy logic, Ambiguity contexts, Standard average internal rate of return, Scale.
The Average Internal Rate of Return (AIRR) is an innovative metric in order to determine cash flow returns related to investments and financing [1]. Its main attribute is its capacity to solve classical inconsistencies that the Internal Rate of Return (IRR) presents in comparison to the Net Present Value (NPV). Though, AIRR does not lose the interpretation advantages that IRR presents related to NPV. Among those inconsistencies, we could mention having multiple rates of returns, setting in order mutually exclusive projects, mutually exclusive projects that have different size scales and reference effects such as value additivity, and different results between expected value from a stochastic IRR and the expected IRR of the investment [2,3]
Besides the importance behind the financial calculator selection while estimating return and value, we must study how we determine uncertainty or ambiguity. In particular, we ought to analyze situations where we do not face complete capital markets. These situations could be faced when we are considering new technologies investments, resource allocation on research and development projects, closed capital real asset investments, or technology-based firms. On these cases where we do not have market information, risk abandons its market condition to be private. Authors classify risks in “market” and “private.” Market risk prices come out of replicating financial portfolio volatility (standard deviation) that imitates project cash flow expected movements. Private risk prices are those where replicating portfolios does not exist since capital markets are not complete. Thus, there is not enough information for its quantification [4]. Indeed, either ambiguity or vague data available are the usual and restrictions of financial valuation. This situation makes it difficult to implement classical probabilistic metrics [5] used while quantifying investment uncertainty (risk). This is how its treatment from a fuzzy logic perspective [6,7] emerges as a complementary alternative to the probabilistic approach. On these adaptations, traditional financial models are adjusted to the mathematical fuzzy logic [2,8-13].
As a motivation to solve this inconvenient, we pretend to develop a didactic article introducing the AIRR [1-3] metric and using it under a fuzzy approach. Our paper follows the following structure: we present main concepts related to AIRR and some of their variants. Afterwards, we summarize fuzzy numbers concepts and their main operations in order to, then, advance into the fuzzy AIRR. Through a hypothetical case analyzes, we study: the congruence of AIRR and NPV while facing different scale exclusive projects; and setting inconsistencies of the expected IRR on expected cash flow IRR. This last situation is solved by the AIRR. Continuing with the selected case, we apply fuzzy AIRR comparing obtained results with those of NPV and fuzzy IRR.
Starting from a sequence of capital and benefits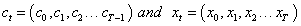 
related to an investment, its result could be expressed as the following:
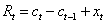(1)
Where term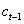 
represents invested capital (borrowed) on period
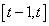and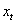 
is cash flow on each period, being 
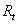the result of the period, subjected to
Period t capital is equal to the product between previous period capital and its rate of return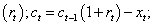 
Initial cash flow is equal to initial investment on the project cash flow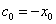
Capital value at the end of the life investment is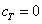 
We assume that in final state (T) there is not growth from reinvestment, and we recover the investment, thus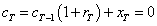 
Periodic rate of return related to the investment comes out from the following expression: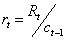 
We assume that invested capital experience increments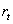 
, explained by 
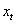being the cash flow measure (obtained/payed). From a given capital flow (c) and cash flow (x), we set the following equality:
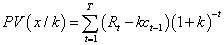(2)
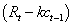expresses extraordinary earnings from the investment which is, in other words, the surpassing between the expected period benefits and normal earnings. These normal earnings are calculated as the product between market rate of return k for investments having similar risk and initial capital 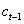. This precedent concept is related to a group of firm valuation models known as residual income [14,15] Reordering previous equation, we get the following expression:
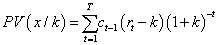(3)
From a formal point of view, the mathematical argument where AIRR is based on is given by the Chisini mean [15]1. Applying the mean concept, AIRR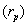 
indicates average returns related to rate rt from equation (3). In order to derive AIRR, it requires the following equality:
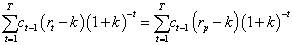(4)
Mean value on the equation is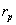 
which is the periodic returns weighted average rt , where these weights are explained by the required capital present value. The decision rule depends on:
If 
If 
Considering the residual income flow from equations (2) and (3), we reach the following expression:
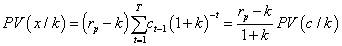(5)
AIRR is different from the Hazen proposal [18,19] because the residual margin is represented by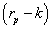 
and not by the difference 
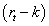. This is a consequence that IRR 
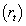is substituted by AIRR 
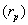.Since it is a mean, AIRR 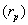does not vary on capital magnitude changes 
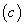as long as 
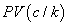remains constant. Proceeding to clear our previous equation based on our 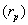variable, we arrive to the operative format of the measure:
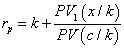(6)
AIRR is a hyperbolic function of 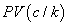,and it is associated with infinite cash flow combinations which generates the same 
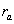for every 
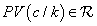In contrast to IRR, 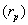is defined for every value
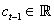.Also,
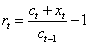is not defined for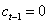 
This return alternative measure is expressed as the project earnings present value divided by capital cash flow present value:
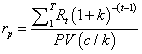(7)
One of the most important characteristics is that AIRR allows us to solve one of the main IRR weaknesses while setting in order mutually exclusive projects with different magnitude. IRR criteria are equal to the NPV ones [1] Considering two projects with cash flow x and y, cash flow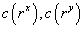 
,and 
its NPV is determined by 
and 
,respectively. IRR election criteria determine that the higher the return, the better position the project gets. However, this measure presents serious inconsistencies while setting in order mutually exclusive projects with different magnitudes under the NPV method. AIRR solves these inconsistencies making congruence with the NPV order criteria. When different magnitudes appear, we proceed to scale the measure. In order to do this, we must estimate capital present value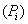 
related to 
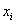projects i =1,2…n.Also, we must define comparable capital magnitude 
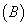also known as minimum investment unit. Standard AIRR (SAIRR) measure is expressed as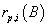 
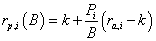(8)
Where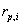 
represents the project AIRR congruent with the NPV order criteria since it is under the condition 
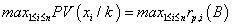.This result must be interpreted as the adjusted weighted average return per comparable capital unit (B).
An inconvenient that we do not take into account very often appears when we study risky alternative investments. On these cases, there is not concord between expected value of the stochastic IRR calculated
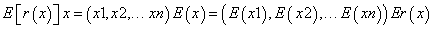
and expected investment cash flow IRR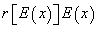 
. The question is: should we first determine expected value of cash flows and then calculate IRR, or should we first determine IRR for each cash flow and then estimate expected value of IRR? These different analyzes lead us to different rates. These inconsistencies while working with capital and cash flow NPV division is not presented between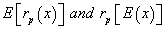 
Fuzzy Average Internal Rate of Return (FAIRR)
Through this section, we will develop AIRR and SAIRR adapting them to fuzzy logic in order to use these return metrics in those situations where data is ambiguous or vague. Firstly, we expose basic operations with triangular fuzzy numbers. Then, we develop the fuzzy version with return measures.
Fuzzy Number and Operations in 
Fuzzy math knowledge is supported by a multivalent logic, in contrast to the bivalent logic of conventional math and probability calculations. Fuzzy math recognizes that a magnitude could adopt wide values of grays between black and white from Aristotle’s logic. Among useful concepts, we must highlight an extremely important one in order to estimate under uncertain environments: the triangular fuzzy number (TFN).
A fuzzy number could be presented in two manners [20]. First, we could assign an interval 
to every level a of presumption (possibility), such as:
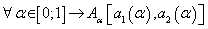(9)
Alternatively, we could present it as a function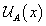 
that represents levels of trust α from a fuzzy number for each value 
. We must determine function 
from central value to the left, and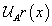 
from central value to the right. These resultant functions are 
:
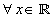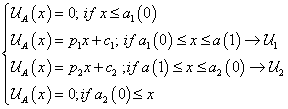(10)
Clearing2 x from membership function to the left and right, respectively, related to α, we obtain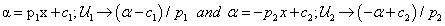 
. If we replace α by the expected number, we get 
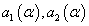thus, the fuzzy number is represented as
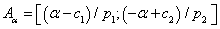(11)
Subsequently, we will present basic operations for a cuts.
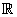
Given two fuzzy numbers
,its addition is set in the following manner:
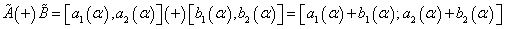(12)
We calculate interval inferior and superior limits, and we proceed to add the resulting values .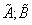
Fuzzy numbers subtraction in
The subtraction3 , 
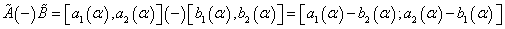(13)
Fuzzy numbers multiplication in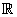
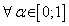
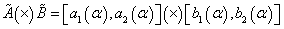
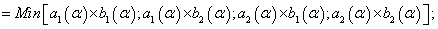
The multiplication4,
(14)
Fuzzy number multiplication by a real number (k)
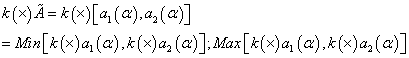(15)
Fuzzy number inverse
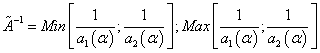(16)
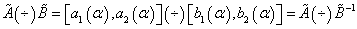
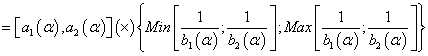
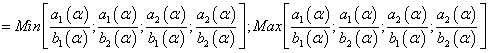(17)
Fuzzy number division by a real number (k)
(18)
From equation 6, we improve AIRR into a new fuzzy version. Its synthetic expression is
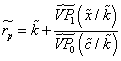(19)
Fuzzy variables are constituted by fuzzy cash flows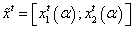 
, fuzzy discount rate 
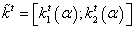, and its fuzzy capital flow 
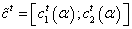. To the previous expanded version, we arrive by applying these operations with fuzzy numbers. We calculate them using the following equation:
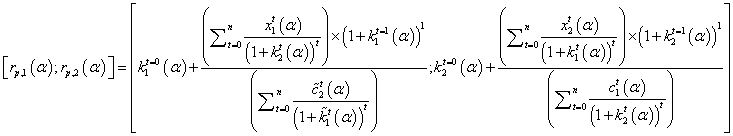(20)
In case we standardize this expression for a capital magnitude B while facing mutually exclusive alternative (i=1, 2, …, n) which have different magnitudes, this is set as
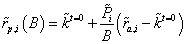(21)
Since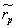 
is a fuzzy number in terms of equation (9), it is interesting to know its crisp mean value (CMV). This is determined by calculating coefficient λ ε [0,1] and solving the defined integral
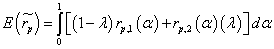(22)
Coefficient λ is known as a pessimism-optimism weighted index [21]. Since it is a TFN, previous expression is reduced to
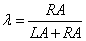(23)
Being RA the “optimism” triangle right area and LA the “pessimism” triangle left area. Once we estimate this index, we are ready to calculate the AIRR mean fuzzy value:
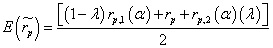(24)
We should not miss that, in contrast to a regular mean, this incorporates the highest area value (RA, LA) related to the TFN.
On this section, we illustrate AIRR behavior while facing IRR and its consistency with NPV criteria onmutually exclusive projects of different size or scale. Next, we will compare consistency between AIRR expected value and project expected cash flows of AIRR. Finally, we will present how it works in mutually exclusive fuzzy project selection related to investments where decision makers face vagueness, ambiguity, and lack of data.
Table 1 presents cash flow (x) and capital flow (c) related to two mutually exclusive investments alternatives (A and B) with different size.
Table 1: presents cash flow (x) and capital flow (c) related to two mutually exclusive investments alternatives (A and B) with different size.
Assuming a cost of capital (k) of 5% per period for both projects, we set in order alternatives applying NPV and IRR criteria: NPVa=$165.10; NPVb=$85.26; [selection using NPV; A> B] ra=17.87%, rb=26.97% [selection using IRR; B> A ]. In order to determine AIRR and SAIRR, we apply equations (6) and (8), respectively. We define $100 as comparable capital unit (B). Results are presented on Table 2.
As we observe on Table 2, even though AIRR presents similar inconvenient to IRR on different size cases, these problemsare solved measure scaling by determining comparable capital unit (B). SAIRR results set projects in order consistent with NPV, A > B .
Table 2: Net Present Value, AIRR, and SAIRR.
Once we selected project A, we analyze value and return variability facing three possible scenarios (optimistic, base, and pessimistic). Occurrence probability associated to each scenario, cash flow, return rates, and expected cash flow are exposed on Table 3. Expected IRR is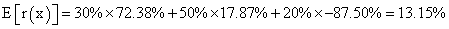 
.Expected cash flow rate of return is 
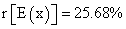. Depending on the cost of capital, an ambiguous situation is generated by the measure inconsistency since 
.
Table 3: Project cash flow and possible scenarios.
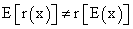This problem is solved by AIRR. On Table 4, we illustrate calculations for project A on the three proposed scenarios, assuming a capital flow c0=800; c1=242.96 c2=186.37 c3=169.68.
Table 4: Expected AIRR.
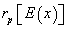is determined from the expected cash flow E(x)= x1=595; x2=290; x3=85; x4=250. On Table 5, we present calculations.
Table 5: Expected cash flow AIRR.
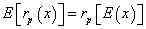and, therefore, it does not drive to reference rate problems in making the accept-reject decision. On this case, with k=5%, project is accepted.
In order to estimate the fuzzy rate, we must determine cash flow and investment cash flow variabilities for the projects, and consequently, its value-intervals. We will determine these intervals through experts’ judgments. With the aim of doing this, we assume that the interval explains variability related to xi and, consequently, ci is given by [α1=1-σ; a=σ; α2=1+σ; α1=0.7; a=0.3; α2=1.3].
We define TFN, as we show in equation (9),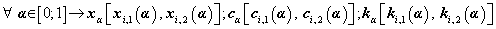 
.On the annex, we present values related to α - cuts of variables 
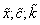.Cost of capital remains constant through all periods. In order to estimate fuzzy NPV, we use the following expression: 
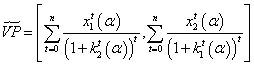.Fuzzy IRR is estimated by
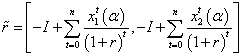. For AIRR and SAIRR, we use equations (20) and (21). On the following Tables 6 and 7, we present different values for the alpha-cuts. On Tables 6 and 7, we present results related to TFN of each metric. In particular, because of the scope of this paper, we illustrate these fuzzy values with AIRR and SAIRR criteria for each project in Figures 1 and 2.
Figure 1: Triangular fuzzy AIRR for each project.
Figure 2: Triangular fuzzy SAIRR for each project.
Table 6: Project A alpha-cuts NPV (x/k), IRR, NPV (c/k), AIRR, and SAIR.
Table 7: Project B alpha-cuts NPV (x/k), IRR, NPV (c/k), AIRR, and SAIRR.
As we can see, both metrics are consistent with setting projects in order criteria. On Table 8, we place these results in order.
Table 8: Capital flow present value, cash flow, IRR, AIRR and SAIRR.
On the PV case, values are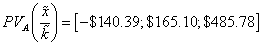 
and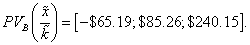 
SAIRR values are (E)rpA = [−141.80%;178.36%;681.42%] , and finally (E)rpB = [−63.2%;94.52%;265.24%] .
On we determine coefficients λ (equation 23), we estimate CMV through equation (24).
On this preceding Table 9, we present how λ>(1-λ), contrary to a probabilistic mean, CMV captures TFN positive bias contained in a defined value.
Table 9: CMV, cash flow present value, capital, IRR, AIRR, and SAIRR.
This paper makes a contribution by connecting tools to measure projects’ returns. It presents AIRR and SAIRR in order to improve IRR weakness as a financial indicator. It used fuzzy logic which is of great importance in contexts of vagueness, ambiguity, lack of information, among others, that affect its capacity of forecasting cash flow precisely.
On the one side, AIRR and SAIRR solve IRR problems without losing its communication and comprehension ability. On the other side, a fuzzy analyzes offers additional information to traditional project valuation. It would only give us results according to presumption α = 1, related to the most possible scenario.
Even though we could find papers that approach these traditional return metric problems and the advantages of a mean rate [1,3]), this article contributes from numerous perspectives. It develops, from a didactic point of view, metric consistency while setting in order mutually exclusive projects of different size or scale; its congruency as an expected rate or a rate over an expected cash flow; and its versatility to adequate itself to the fuzzy logic, keeping its coherence in setting alternatives in order with the NPV.
Menu