ISSN: E 2347-226X, P 2319-9857
ISSN: E 2347-226X, P 2319-9857
Olalere Olusegunbayomi*,lara Oluwaseun Ruth, Mohamed Saad Bala, Mohamed Farag Twibi
Chemical & Natural Resources Engineering, University Malaysia Pahang, Lebuhraya Tun Razak, 26300 Kuantan, Pahang, Malaysia
Received date: 08/06/2016; Accepted date : 02/08/2016; Published date: 09/08/2016
Visit for more related articles at Research & Reviews: Journal of Agriculture and Allied Sciences
The development of feed formulation is essentially a problem of optimization which involves selecting the best alternative, starting from a specified set of possibilities. This study is aimed at developing a generic decision supporting system for optimizing the poultry feed production through the application of multi-objective proximal bundle approach, taking into consideration the energy optimization, limiting the amino acid variation and providing a least cost of production. A non-differentiable interactive multi-objective bundle-based optimization method was used in solving this problem. This technique provided a wide range of alternatives choices for the decision maker to formulate an effective and optimum feed that will minimize the costs, achieve more balanced ration, limit the methionine variation for growth, and optimize the metabolized energy based on feed at his/her disposal. The algorithm of this method is based on the objective functions classification. According to this classification, a new (multi-objective) optimization problem was formed and solved by a Multi-objective Proximal Bundle method. The method in turn generated different alternative formulations from which the decision maker arrived at the final decision. The results were displayed as value path according to their range of values, and from the lists of alternatives, it is clear that none of the alternatives can be better improved without impairing others. At this point the decision maker will now make a choice from the list, based on his preference. This is done by ranking the three objectives according to the decision maker’s order of preference. The decision maker must therefore be willing to sacrifice something. This work therefore provided a platform to provide solution to the problem of conflicting objectives of energy optimization, limiting amino acid variation and ration cost minimization in feed formulation.
Optimization, Feed, Chick-Mash, Poualtry feeding, optimal solutions.
Feed is one of the factors which playn integral role in determining successful development of livestock production. Feed formulation on the other hand is the process of measuring the quantity of feed ingredients that need to be put together, to form single uniform mixture (diet) that suppliesll of poualtry nutrient requirements [1]. It is one of the fundamental operations of the poualtry production, which ensures that feed ingredientsre economically harnessed for optimum growth of the chickens. This requires a good knowledge of poualtrynd feed ingredients [2].non [3] investigated the factors involve innimal feed ration formulating to include the Cost of feed Ingredients, feedcceptability to thenimal,bility of thenimal to digest the formulated feednd the percentage of toxic substances in the feed. The development of feed formulation is essentially problem of optimization which involves selecting the bestalternative, starting from specified set of possibilities. Due to the various constraints that needed to be considered, the feed mix has been increasingly difficualt. It is then critical to produce the bestnimal diett minimum cost in order to trim down the operational costnd gain more profit. The development of satisfactory diet in livestock production, demands comprehensive understanding of their nutritional requirementsnd the quality of the ingredients that comprise the feed [4]. Nutritional characteristics of the diet formulated include ingredient selectionnd the nutrient level.
The followingre the problemsssociated with feed formulation ingredient variability, price variability,nd nutrient imbalances of different ingredients [5].
Waugh [6] was the first researcher whottempted to solve the feed mix problem using mathematical programming. For the first time he optimized livestock ration in economic terms using linear program. This method had been employed in feed production to determine the minimum cost formulation that will respect the specified constraints. Hence, linear program is used for feed formulation of single criterion. In search for the best formulation, the main objective is to determine the optimum levels of the components or key ingredients. The ingredients (feed inputs)re the independent variablesnd the dependent variables (quality performance measure or responses)re the factor to be optimized (maximized or minimized). When various responses are involved, the term combined response optimization is preferable
The primaryim of using mathematical program tool is tossist breeders, in formulating ration that is both from nutritional nd from economic viewpoint more efficient. It could inddition be usedlso tossess the variable cost of feed used. The minimum cost formulation, frequently sacrifices the quality of the products productcceptability is not, usually, linear function of the ingredients.n important complicating factor present in most problems concerning feed formulations is the existence of limitations or constraints. The mualti-objective optimization problems usually have many optimal solutions, knowns pareto optimal solutions. Each parent optimal solution represents different compromisemong design objectives. Hence, the designer is interested in finding many pareto optimal solutions in order to select design compromise that suits his preference structure. Therere number of different methodsvailable for solving mualti-objective optimization problems. One popularpproach is condensing mualtiple objectives into single, composite objective function by methods suchs the weighted sum, geometric mean, perturbation, tchybeshev, min-max,nd goal programming.notherpproach is to optimize one objective while treating other objectivess constraints. Thesepproaches give one pareto optimal solution in each simulation.
The extreme cold weather condition is the major cause of death in poualtry farms.nd in spite of the measures been taken to control this; the problem keeps unabated.nccuratend efficient maximization of metabolizable energy is therefore necessity when formulating poualtry feed [7]. Energy maximization should therefore be considered moresn objective rather thans constraint. The limiting essentialminocid (methionine) islso of paramount important due to its function in body proteins synthesis. It is constituent of many body parts, suchs muscles, organs, integumentnd feathers.ll the three objectivesre put together in order to meet the nutrient required of thenimal, bearing in mind the cost of production. In line with thebove statement the mualtiple-objective programming (MOP) model is flexiblealternative when handling these conflicting objectives [2].
The energy in poualtry feed is expressed world-wide in terms ofpparent metabolizable energy, The energy contents of components for complete dietsre commonly expressed in kJ or MJ (occasionally in kcal).
Andequate supply of energyt lowmbient temperatures islways major challenge.nd with decreasingmbient temperature, chicks energy demand increases resistance ton extreme cold .Hence the energy demand by the chick mash is in inverse proportion tombient temperature.t low temperature, when the daily intake islready low, the hens will reduce their intake less in response to increased energy concentration of feed, with the net effect of increased energy intake [8]. Lazo etl. [4] proposed range of energy systems that might be considered for the formulation of poualtry feeds, these include digestible energy, metabolizable energy,nd net energy.
On the other hand, the sulphurminocid isn integration of methioninend cysteinend thesere involved in complex metabolic processes [9]. Methionine performs the function of proteins body synthesisnd is constituent of many body parts, suchs muscles, organs,nd feathers. It islso involved in functions unrelated to protein synthesis, suchs the synthesis of polyamines [10].nd despite the important role played by methioninend lysine in poualtry feed formulation, it is not without side effects, hence the need to optimize them such that we will not under-formulate or over-formulate their diets [11].
This paper shows the development of web-based generic decision support system for poualtry feeding. This study isimed t developing generic decision supporting system for optimizing the poualtry feed production through thepplication of mualtiobjective proximal bundlepproach, taking into consideration the energy optimization, limiting theminocid variationnd providing least cost of production. The benefit ofpplying this method is that, it offers more efficient solution for the optimal combination of ingredients, when compared to linear programmingpproach [12].
Many methods of formulating chick feeds exist. The methodpplied in this project is the non-differentiable interactive mualtiobjective Bundle-based (NIMBUS) optimization method. Thelgorithm of NIMBUS method is based on the objective functions classification. The optimization of the metabolizable energy; ration cost,nd limitingmino-acid is solved iteratively using this method. For the individual iteration, the decision maker (user) issked to classify the objective functions into up to five different classes. The development of mualti-objective programming model for feed formulation model that will maximize metabolized energy, minimize ration costndminocid is therefore the focus of this chapter. NIMBUS is one of the most commonly used mathematical optimization model required to solve conflicting objectives for the decision maker has beendopted. The feed formulation problem was studied for insight into the underlining interactions. Systems variables were identifiednd constraints characterized. The problem consists of eight variables, seven constraints,nd three criteria.
The respective quantities of feed ingredient (i.e., the decision variables) in the formulation of poualtry feedres defined in Table 1
| Decision Variable Symbols | Feed Ingredients |
|---|---|
| x1 | Whole Corn |
| x2 | Sorghum |
| x3 | Soya |
| x4 | Groundnut |
| x5 | PKC |
| x6 | Bone Meal |
| x7 | Rice bran |
| x8 | Oyster |
Table 1: The decision variables representing the quantities of feed ingredients
The three functions taken intoccount in this problem include the cost, energynd methionine variation Functions.
• Energy Function
According to Olomu [13], the metabolizable energy is the easiestnd most convenient to derive in poualtry. It is derived from the formula, ME=DE-UE, Where UE is the urinary energynd DE is the digestible energy. Hence, the objective of this model is to maximize the energy contentgainst extreme cold. This is givens:
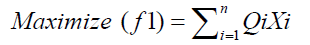 (1)
(1)
• Ration Cost Function
The cost functionsn objective is given by:
 (2)
(2)
• Limitingminocid Variation
The minimization ofminocid in the feed is given by:
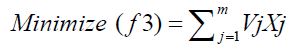 (3)
(3)
• The Problem Constraints
The constraints interval of the minimum to maximum nutrient requirements is givens:
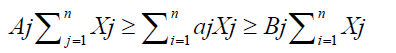 (4)
(4)
The compositional Constraints is the sum total ofll the ingredients in the formulation. It could be expressed in terms of percentage or the total.
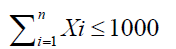 (5)
(5)
Where i=1…..n, j=1……..m
This involves the gathering of feed data needed for study. The nutrient content of the feed ingredients, the range of values of feedstuff, the required specificationnd the cost of ingredients were obtainednd prepared. Ration cost of the ingredients were gotten from the current market price of feed ingredient in Nigeria. Different nutrients were provided with individual maximum and minimum dietary inclusions for fat, fiber, calcium, phosphorus, proteinnd lysine. The data gotten is presented in Tables 2-5.
| Nutrients | Fat | Fiber | Calcium | Phosphorus | Protein | Lysine |
|---|---|---|---|---|---|---|
| Percentage Value | 3.5 | 5.0 | 1.0 | 0.45 | 20 | 1.0 |
Source: Feed Formulation Guide (1998)
Table 2: Productionims for chick mash
| Ingredients | Corn Grain | Sorghum | Soya Bean | Groundnut | PKC | Bone Meal | Rice Bran | Oyster |
|---|---|---|---|---|---|---|---|---|
| Cost(Naira per Kg) | 54 | 50 | 78 | 61 | 13 | 33 | 12 | 12 |
Table 3: Cost of ingredient per kilogram
| Raw Nutrient | Corn | Sorghum | Soya | GroundNut | PKC | BoneMeal | Rice Bran | Oyster Shell |
|---|---|---|---|---|---|---|---|---|
| Fat | 4.00 | 5.00 | 2.00 | 6.00 | 6.00 | - | 12.50 | - |
| Fiber | 2.00 | 6.00 | 6.50 | 5.00 | 12.00 | - | 12.50 | - |
| Calcium | 0.01 | 0.10 | 0.20 | 0.20 | 0.21 | 37.00 | 0.04 | 38 |
| Phosphorus | 0.09 | 0.09 | 0.60 | 0.20 | 0.16 | 1.50 | 0.48 | - |
| Protein | 10 | 9 | 45 | 45 | 18 | - | 12 | - |
| Lysine | 0.25 | 0.25 | 2.8 | 1.6 | 0.64 | - | 0.5 | - |
Source: Feed Formulation Table; National Research Council (NRC) 1994
Table 4: The nutrient level in each ingredient (Constraints Table)
| Raw Obj.Fn | Corn | Sorghum | Soya | Ground Nut | PKC | Bone Meal | Rice Bran | Oyster Shell |
|---|---|---|---|---|---|---|---|---|
| Cost Function | 54 | 50 | 78 | 61 | 13 | 33 | 12 | 12 |
| Energy Function | 3434 | 3300 | 2700 | 2640 | 2175 | - | 2860 | - |
| Methionine Function | 0.18 | 0.18 | 0.59 | 0.48 | 0.39 | - | 0.24 | - |
Source: Feed Formulation Table; National Research Council (NRC) 1994
Table 5: Criterion table.
The chick-mash mualti-objective feed formulation model
The above generalized feed formulation model is a generic model that can be applied using the values from Table 2-5. The mualti-objective function is drawn from Tables 2 and 3 to obtain the following sets of equations shown below. The methionine function is a non-linear function since it represents a variance in the limiting amino-acid, while both the cost and energy functions are linear in nature. The mualti-objectives are given below:
Minimize Cost (f1)=54x1+50x2+78x3+61x4+13x5+33x6+12x7+12x8;
Maximize Energy (f2)=3434x1+3300x2+2700x33+2640x4+2175x5+2860x7; (6)
Minimize Methionine (f3) = 0.18x12+0.18x22+0.59x32+0.48x42+0.39x52+0.24x72;
Using the generalized model the following constraints were obtained as shown below:
Fat: 4x1+5x2+2x3+6x4+6x5+33x6+12.5x7≤3.5;
Fiber: 2x1+6x2+6.5x3+5x4+12x5+12.5x7≤5.0
Calcium: 0.01x1+0.10x2+0.20x3+0.20x4+0.21x5+37x6 +0.04x7+38x8≤1.0
Phosphorus: 0.09x1+0.09x2+0.60x3+0.20x4+0.16x5+1.50x6+0.48 x7≤0.45 (7)
Protein: 10x1+9x2+45x3+45x4+18x5+12x7≤20
Lysine: 0.25x1+0.25x2+2.8x3+1.6x4+0.64x5+0.5x7≤1.0
Composition: x1+x2+x3+x4+x5+x6+x7+x8≤ 1000;
The above is then solved using the NIMBUS web-based database.
Non-differentiable interactive mualti-objective bundle-based optimization system (NIMBUS) approach
The NIMBUS is a mualti-objective optimization system that has the capacity to handle non-differentiable functions and optimize several objectives at the same time, thereby creating a group of different solutions [14]. The decision maker (user) now selects the best solution from a list of Pareto solutions available. This approach allows the decision maker to guide the search by aalternating optimization and preference articulation iteratively [15].
This non-differentiable interactive mualti-objective Bundle-based (NIMBUS) optimization method is therefore suitable in solving this non-linear, feed formulation problem with conflicting objectives [16]. Its algorithm is based on the objective functions classification .With the individual iteration, the decision maker (user) is asked to classify the objective functions into up to five different classes [17].
• Those to be improved,
• Those to be improved till some aspiration level,
• Those to be accepted as they are,
• Those to be impaired till some bound, and
• Those allowed changing freely.
According to the classification, a new (mualti-objective) optimization problem is formed and is solved by an MPB (Mualti-objective Proximal Bundle) method. The MPB method is a generalization of Kiwiel’s proximal bundle approach for non-differentiable single objective optimization into the mualti-objective case. The mualtiple objective functions are treated individually without employing any scalarization [18]. The method is capable of handling several non-convex locally Lipschitz continuous objective functions subject to nonlinear (possibly non-differentiable) constraints [19]. The decision maker is therefore the one to makes the final decision which of the solution is best suitable goals.
Merits of NIMBUS approach
The following are the advantages of NIMBUS method over other mualti-objective optimization methods [17]:
It can balance between several conflicting criteria subject to equality and inequality constraints.
It can analyze the inter-relationship among different objectives.
It has the ability to handle non-differentiable and complicated functions.
A strong point in NIMBUS method is that Pareto optimal solution can be obtained.
It can solve local and global Pareto optima.
Interpretation of resualts
Classification of objectives
Classifying functions is necessary here since we have more than one objective functions to deal with. For one objective function, the optimal resualts will be displayed directly.
Because the solution process with NIMBUS is iterative there is usually not only one absolutely right solution. Hence you are asked to 'guide the solver to a desired direction'. The classification is a process in which the desires of the user are expressed. You can choose which of the function values should be decreased from the current level and which of the functions are less important (i.e., their values can be increased). If the second or the fourth aalternative is selected, you are asked to specify the bounds for the function values; that is, aspiration levels and upper/lower bounds, respectively [17].
Aspiration level: Defines a desired value for the objective function.
Upper/lower bound: Defines the limit value that the function should not exceed, if possible.
Solution concepts used in NIMBUS
• Pareto optimality
A criterion vector z* (consisting of the values of the objective functions at a point x*) is Pareto optimal if none of its components can be improved without impairing at least one of the other components. In this case, x* is also called Pareto optimal. Synonyms for Pareto optimality are efficiency, non-interiority and Edge worth-Pareto optimality [15].
Ideal Criterion Vector and Nadir Vector
• ICV=Ideal criterion vector
The ideal criterion vector consists of the best possible values each objective function can achieve. The ICV represents the lower bounds of the set of Pareto optimal solutions. (That is, Pareto optimal set). From this problem the ICV for each objective is given as:
| Objective Functions | Ideal Criterion Vector (estim.) |
|---|---|
| Cost Function (f1) | 10.00000*E+3 |
| Methionine (f2) | 4.188456E-7 |
| Energy (f3) | 1000.00 |
For minimized functions the ICV was given as the Lowest Value and for maximized functions as the Highest Value.
• Nadir vector.
The Nadir vector estimated the upper bounds of the solutions in the Pareto optimal set. It represented the worst values that each objective function can attain in the Pareto optimal set. The Nadir values for the three objectives are:
| Objective Functions | Nadir Vector (estim.) |
|---|---|
| Cost Function (f1) | 48.92774*E+3 |
| Methionine (f2) | 0.133824 |
| Energy (f3) | 3031.73 |
• For minimized functions the Nadir is given as the Highest Value and for maximized functions as the Lowest Value.
• Since we are dealing with Pareto optimal solutions (compromises) we must be willing to give up something in order to improve some other objective. That is why the classification is feasible only if at least one objective function is in the first two classes and at least one objective function is in the last two classes.
There were five sets of new aalternatives generated by the system. These aalternatives are labeled Aalternative 1….Aalternative 6, as shown in Figures 1-4. From which the decision maker is free to select four that is suitable for him, before a final decision is made. The selected aalternatives are given below:
Aalternative 1 (Criterion vector: (20.31445*E+3, 5.491057E-2, 1772.162))
Aalternative 2 (Criterion vector: (13.37071*E+3, 1.533576E-2, 1019.42))
Aalternative 3 (Criterion vector: (20.34011*E+3, 3.209189E-2, 1658.513))
Aalternative 4 (Criterion vector: (16.36793*E+3, 1.199876E-2, 1086.065))
Aalternative 5 (Criterion vector: (20.09646*E+3, 5.468131E-2, 1780.108))
The aalternative solutions are displayed in Figure 2 as value path according to their range of value for easy consideration by the decision maker. From the lists of aalternatives, it is clear that none of the aalternatives can be better improved without impairing others. At this point the decision maker will now make a choice from the list, based on his preference. This is done by ranking the three objectives according to the decision maker’s order of preference. For instance, if the most preferred criterion vector z* is the cost, then the aalternative 2 with the least cost i.e., (Criterion vector: (13.37071*E+3, 1.533576E-2, 1019.42)) is selected. Here the aalternative2 is selected as the most Pareto optimal based on the least cost. But it should be noted that aalternative2 has energy function from the list of Pareto optimal solution. The decision maker therefore must be willing to sacrifice something.
However if the growth of the chicks is of paramount important to him, then aalternative 1(Criterion vector: (20.31445*E+3, 5.491057E-2, 1772.162)) with the highest criterion amino acid is preferred. However this will increase the cost of feed ingredients. This method was employed by Žgajnar & Kavčič [20] to formulate a nutritionally balanced and economically acceptable ration that also fulfills conditions in pig farming.
The development of feed formulation is essentially a problem of optimization which involves selecting the best aalternative, starting from a specified set of possibilities. The sets of possibilities presented in this work enabled the decision maker to forecast in advance ingredients required for each sets of possibilities.
This technique therefore provides a wide range of aalternatives for the decision maker in order to make an effective and optimum feed formulation.