Keywords
|
| Direct Power Control, Power Factor, PWM Rectifier, Power Quality, THD. |
INTRODUCTION
|
| In recent decades, the increasing use of non linear loads during these last decades induces severe problems. The problem consists on the distortion in current and voltage wave forms. |
| Several harmonics cancellation methods were proposed; the typical one was the connection on the ac side of shunt passive filters. However they are bulky, expensive and resonant. Recently, active filtering and PWM conversion (rectification) are taking their places in industry plants. |
| Development of control methods for active boost rectifiers was possible thanks to advances in power semiconductor devices and digital signal processors, which allow fast operation and cost reduction. It offers possibilities for implementation of sophisticated control algorithms. Appropriate control can provide both the rectifier performance improvements and reduction of passive components which is very important for high power systems. |
| Three-phase pulse with modulated (PWM) rectifiers (AC/DC converters) has grown rapidly due to some of their important advantages such as: power generation capabilities, control of dc bus voltage, low harmonic distortion of input current and high power factor (usually near unity). In recent years different strategies have been proposed [1] [2] for controlling PWM converter. The main goal of these control strategies is to obtain the high power control and sinusoidal current estimated flux signal is used in the control system. |
| Therefore their principles are different. One of these methods the voltage oriented control (VOC), guarantees high dynamics and static performance via an internal current control loops; several papers are published in this field. Consequently, the final configuration and performance of this control largely depends on the quality of the applied current control strategy [3]. The classical Direct Power Control (DPC) is based on the instantaneous active and reactive power control loops [4] [5] [6]. In this method, there are no internal current control loops and no PWM modulator block, because the converter switching states are appropriately selected by a switching table based on the instantaneous errors between the commanded and estimated values of active and reactive power. this method requires a good estimate of the active and reactive powers. |
| This paper covers the existing solution of Direct Power Control and presents a new solution based on Virtual Flux estimation [2]. Theoretical principle of the proposed method is discussed. The steady state and dynamic behaviour of VF-DPC are presented, illustrating the operation and performance of the proposed system as compared with a conventional DPC method. This strategy is also investigated under variation of load and DC voltage reference. It is shown that the VF-DPC exhibits several advantages; particularly it provides sinusoidal line current when the supply voltage is non-ideal. Test results show excellent performance of the proposed system. |
VIRTUAL FLUX ESTIMATION
|
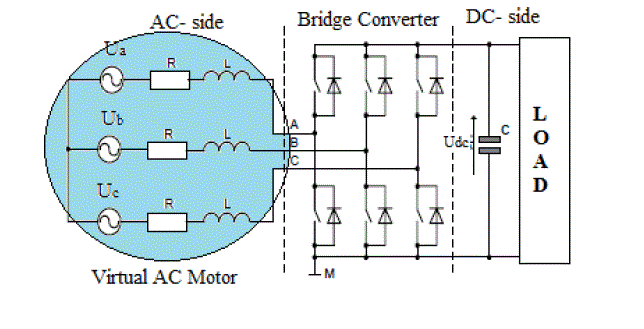
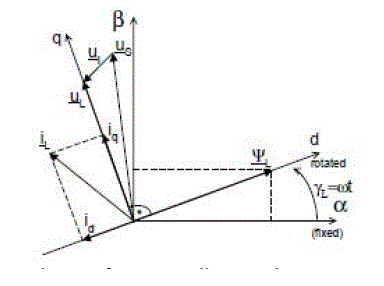
| The voltage imposed by the line power in combination with the AC side inductors are assumed to be quantities related to a virtual AC motor as shown in Fig. 1. |
| Thus, R and L represent the stator resistance and the stator leakage inductance of the virtual motor and phase-to-phase line voltages: Uab, Ubc, Uca would be induced by a virtual air gap flux. In other words the integration of the voltages leads to a virtual line flux vector ΨL, in stationary α-β coordinates (Fig.2). |
| ΨL-virtual line flux vector, US - converter voltage vector, UL - line voltage vector, UI - inductance voltage vector, iLline current vector. |
| A virtual flux equation can be presented as [7], [8] (Fig.3): |
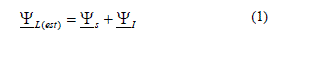 |
| Based on the measured DC-link voltage Udc and the converter switch states Sa, Sb, Sc the rectifier input voltages are estimated as follows: |
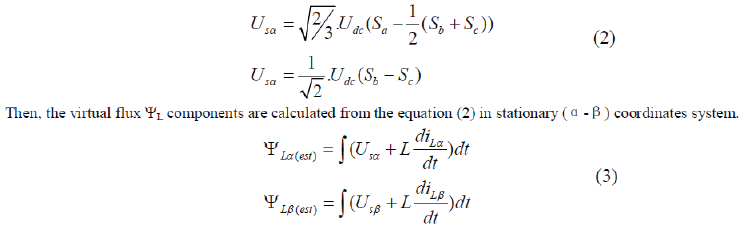 |
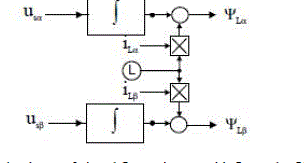
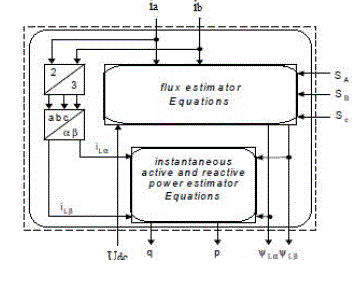
| The virtual flux components calculation is shown in Fig. 4. |
DIRECT POWER CONTROL (DPC)
|
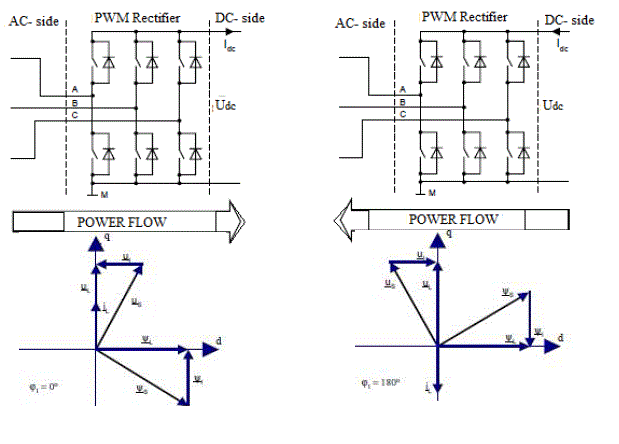
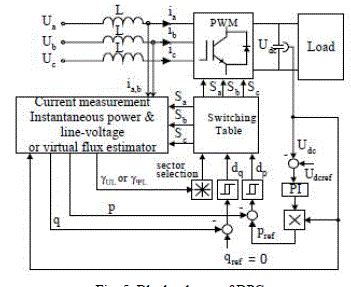
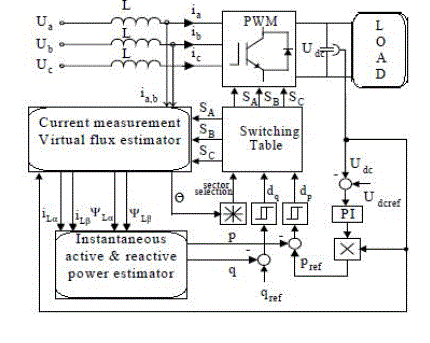
| The main idea of DPC proposed in [10] and next developed by [9] is similar to the well-known Direct Torque Control (DTC) for induction motors. Instead of torque and stator flux the instantaneous active (p) and reactive (q) powers are controlled (Fig.5). |
| The commands of reactive power qref (set to zero for unity power factor) and active power pref (delivered from the outer PI-DC voltage controller) are compared with the estimated q and p values, in reactive and active power hysteresis controllers, respectively. |
| The digitized output signal of the reactive power controller is defined as: |
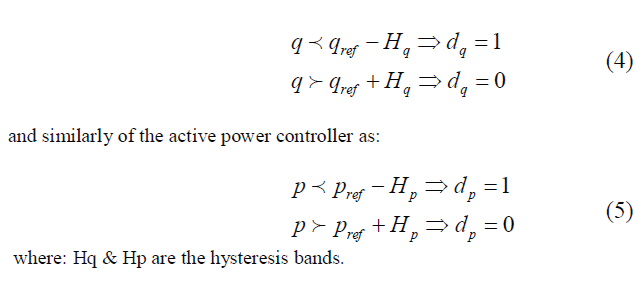 |
| The digitized variables dp, dq and the voltage vector position γUL = arc tg (ULα/ULβ) or flux vector position γΨL = arctg (ψLα/ψLβ) form a digital word, which by accessing the address of the look-up table selects the appropriate voltage vector according to the switching table (Table I). |
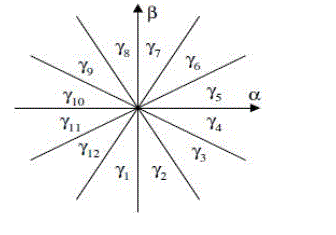
| The region of the voltage or flux vector position is divided into twelve sectors, as shown in Fig. 6 and the sectors can be numerically expressed as: |
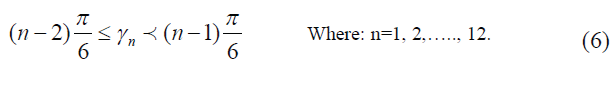 |
| Note that the sampling frequency has to be about few times higher than the average switching frequency. This very simple solution allows precisely control of instantaneous active and reactive power and errors are only limited by the hysteresis band. No transformation into rotating coordinates is needed and the equations are easy implemented. This method deals with instantaneous variables, therefore, estimated values contain not only a fundamental but also harmonic components. This feature also improves the total power factor and efficiency [10]. |
| Further improvements regarding VF-DPC operation can be achieved by using sector detection with PLL (Phase-Locked Loop) generator instead of zero crossing voltage detectors (Fig. 7). This guarantees a very stable and free of disturbances sector detection, even under operation with distorted and unbalanced line voltages. |
POWER ESTIMATION BASED ON VIRTUAL FLUX
|
| The Virtual Flux (VF) based approach has been proposed by Author to improve the VOC [11], [12]. Here it will be applied for instantaneous power estimation, where voltage imposed by the line power in combination with the AC side inductors are assumed to be quantities related to a virtual AC motor. |
 |
 |
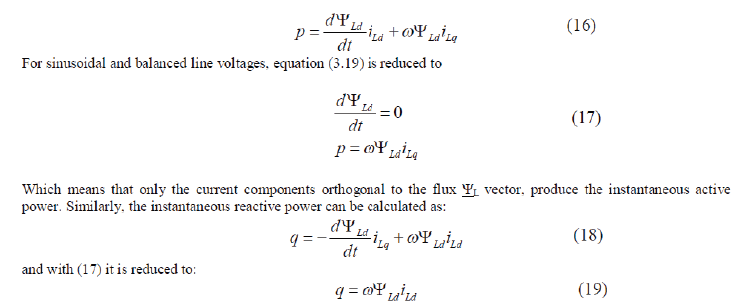 |
| However, to avoid coordinate transformation into d-q coordinates, the power estimator for the DPC system should use stator-oriented quantities, in α-β coordinates (Fig.4). |
| Using (14) and (15) |
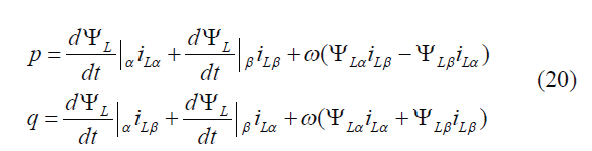 |
| For sinusoidal and balanced line voltage the derivatives of the flux amplitudes are zero. The instantaneous active and reactive powers can be computed as [13], [14]. |
| The measured line currents ia, ib and the estimated virtual flux components ΨLα, ΨLβ are delivered to the instantaneous power estimator block (PE) as depicted in Fig.8. |
DC VOLTAGE REGULATION
|
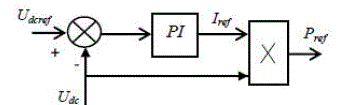
| In the proposed DPC scheme, magnitude of fundamental input currents is delivered from the outer proportional-integral (PI) dc-bus voltage controller and will be multiplied by the dc voltage to obtain the reference of the instantaneous active power. |
| To have unity power factor condition, reference reactive power must be equal to zero. |
| The regulation function is ensured by a PI corrector shown in the figure below: |
| Where Kp and Ki are the proportional and integral controller gains respectively. |
| To determine the parameters of the PI controller, we make the following mathematics development. |
| The relationship between the power absorbed by the capacitor and the terminal voltage can be written: |
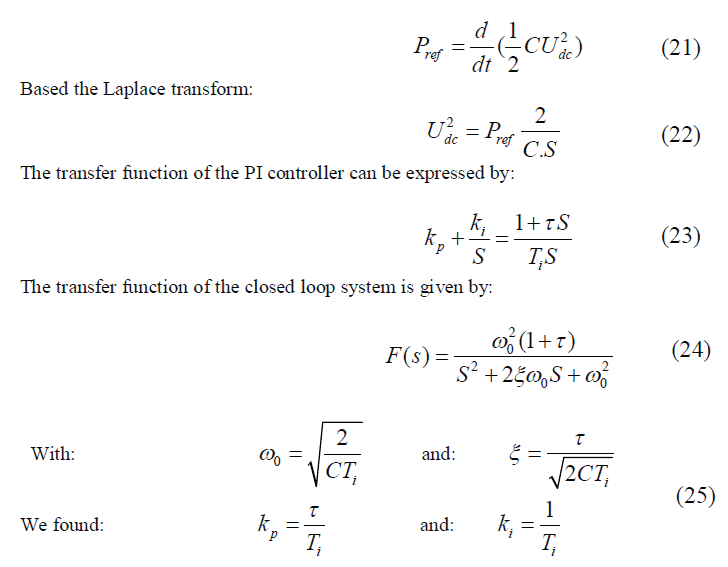 |
RESULTS AND DISCUSSION
|
| To study the operation of the virtual flux based DPC/PWM rectifier, it is implemented in MATLAB/SIMULINK environment. The simulation results obtained for different conditions show in fig 10 to 12. Simulations have been carried out using the main electrical parameters of power circuit and control data showed in Table II. |
| Several tests were conducted to verity feasibility of the proposed technique. Fig 10 shows the simulated waveforms under unity power factor operation in the steady for purely sinusoidal supply line voltage. |
| From this figure, it can be seen that the line currents are very close to sine wave (Fig. b) and in phase with the power source voltages (Fig. c) because the reactive power command qref is set to zero (Fig. f). The active power is constant on average (4.6KW). The reactive power is zero on average because of the unity power factor operation. |
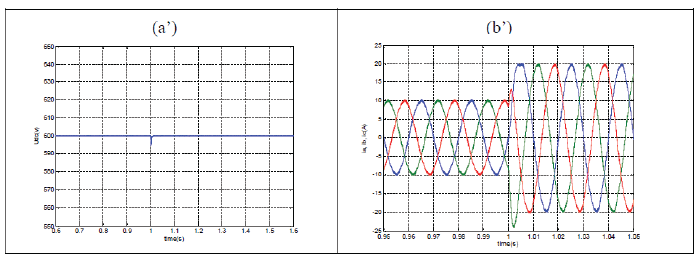
| The effect of dc side load on the operation of system is shown in figure 11. As shown in these figure the change in load don’t affect DC link voltage and only change the amplitude of the line current and the line side active power. |
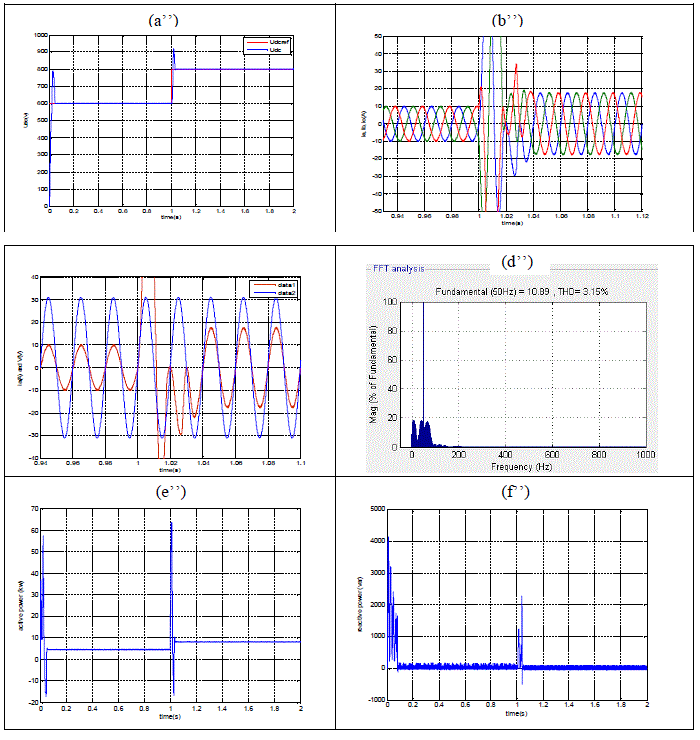
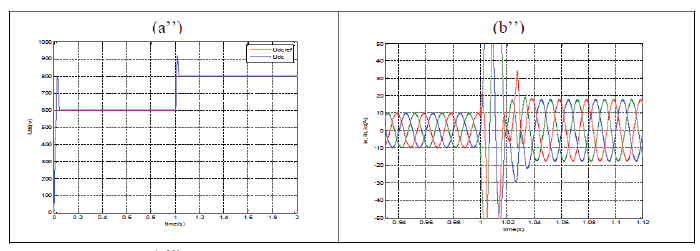
| Fig.12 Show that when the DC voltage reaches the new reference value (Fig. a’’), the active power and consequently the line current increase (Fig. b’’). At the moment of DC step variation reactive power is sensibly reduced. The line voltage and current are almost in phase (fig .c’’), and thus the power-factor is almost equal to 1. In the case the wave shape of the line current close to the sinusoid, and hence the THD= 3.15%. In order to maintain the continuous bus charged, the DC voltage variation involves a reference variation in the instantaneous active power. |
CONCLUSION
|
| Regarding the advantages of PWM rectifier, in this paper a new control strategy of PWM rectifiers is presented and discuted. To predict behaviour of DPC/PWM rectifier in different load, dynamic model is implemented in matlab/simulink. This method uses the estimated Virtual Flux (VF) vector instead of the line voltage vector. Consequently, voltage sensorless line power estimation is much less noisy thanks to the natural low-pass behaviour of the integrator used in the calculation algorithm. Also, differentiation of the line current is avoided in this scheme. So, the presented VF-DPC of PWM rectifier has the following features and advantages: |
| - no line voltage sensors are required, |
| - lower sampling frequency (as conventional DPC), |
| - sinusoidal line currents (low THD), |
| - no current regulation loops, |
| - high dynamic, decoupled active and reactive power control, |
| - Simple algorithm |
| It is an important advantage of this converter particularly in speed control drive system that the operation of drive should be robust for line voltage disturbed conditions. As simulation results show, the reactive power is programmable in this system and can be set to obtain unity power factor. Also the lines current have sinusoidal wave form. |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
 |
 |
 |
 |
 |
| Figure 6 |
Figure 7 |
Figure 8 |
Figure 9 |
Figure 10 |
 |
 |
| Figure 11 |
Figure 12 |
|
References
|
- J.L. Duate, A, Van Zwam, C, Wijinands, A.Vandenput “Reference frames fit for controlling PWM rectifiers”. IEEE Trans. On Ind.Electronics, Vol.46, No.3, pp. 628-630, 1999.
- S.Hansen, M.Malinowski, F.Blaadjerg, M.P. Kazmiekowski, ”Cotrole strategies for PWM rectifiers without line voltage sensors”, IEEEAPEC,2000.
- M.P. Kazmierkowski, L.Malesani, “Current control techniques for three phase voltage source PWM converters: a survey”, IEEE Trans. On Ind. Electronics, Vol.45,No,5,pp.691-703,1998.
- L. Angquist, L. Lindberg, “Inner phase angle control of voltage source converter in high power application” in proc. IEEE-PESC Conf., pp. 293-298,1991
- M. Malinowski, M.P. KaÃâ¦Ãºmierkowski, S. Hansen, F. Blaabjerg, G. D. Marques, “Virtual flux based Direct Power Control of three-phase PWM rectifier” , IEEE Trans. on Ind. Applications, vol. 37, no. 4, pp. 1019-1027, Jul/Aug 2001.
- V. Manninen, “Application of Direct Torque Control modulation technology to a line converter”, in Proc. EPE Conf., Sevilla, pp.1.292-1.296, 1995.
- V. Valouch, J. Skramlink, “Analysis of direct self control in voltage type PWM rectifier” in proc. EPE Conf., pp.3.195-3.199, 1997.
- M. Weinhold, “A new control scheme for optimal operation of a three-phase voltage dc link PWM converter”, in proc. PCIM Conf., pp.371-3833, 1991.
- S. Bhattacharya, A. Veltman, D. Divan, R.D. Lorenz, “Flux-based active filter controller” IEEE Trans. on Ind. Application, vol. 32, no.3, pp.491-502, May/June 1996.
- T. Noguchi, H. Tomiki, S. Kondo, I. Takahashi, “Direct Power Control of PWM converter without power-source voltage sensor” IEEE Trans. on Ind. Applications, vol.34, no. 3, pp. 473-479, May/June 1998.
- T. Ohnishi, “Three-phase PWM converter/inverter by means of instantaneous active and reactive power control” In proc. IEEE-IECON Conf.,pp. 819-824, 1991.
- J. L. Duarte, A. Van Zwam, C. Wijnands, A. Vandenput, “Reference frames fit for controlling PWM rectifiers” IEEE Trans. on Ind.Electronics, vol. 46, no. 3, pp. 628-630, 1999.
- P. J. M. Smidt, J. L. Duarte, “An unity power factor converter without current measurement”, in proc. EPE Conf., Sevilla, pp. 3.275-3.280,1995.
- M. Malinowski, M.P. KaÃâ¦Ãºmierkowski, S. Hansen, F. Blaabjerg, G. D. Marques, “Virtual flux based Direct Power Control of three-phase PWM rectifier”, IEEE Trans. on Ind. Applications, vol. 37, no. 4, pp. 1019-1027, Jul/Aug 2001.
- M. Malinowski, M. P. KaÃâ¦Ãºmierkowski, A. Trzynadlowski, “Direct Power Control with virtual flux estimation for three-phase PWM rectifiers”In proc. IEEE-ISIE Conf., Puebla, pp. 442-447, 2000.
|