A New Piecewise Dynamic Constitutive Equation of Powder Metallurgy High Speed Steel

Abstract

In order to optimize the hot working technology of powder metallurgy high speed steel, The hot deformation behavior of powder metallurgy (PM) high speed steel was investigated by Gleeble-1500D simulation at the temperature range of 1000-1150°C, strain rates between 0.001 s-1 and 1.0 s-1 and deformation rate of 60% of the samples. The flow stress under different temperatures and strain rates were analyzed. The results show that the flow stress is influenced strikingly by deformation temperature and strain rate. Both the peak stress and the corresponding strain decrease with the increase of temperature and the decrease of strain rate. Deformation temperature, strain rate and deformation activation energy have a great affect on the microstructure. The value of deformation activation energy is 750.67 kJ/mol. The mathematical model of the strain corresponding to the peak stress was set up. The relationship between the strain corresponding to the peak stress and the strain corresponding to the critical stress can be described as: εc=0.606 εp. The segmental dynamic constitutive equation under different strain was established based on the idea of subsection.

Keywords

Powder metallurgy, High speed steel, Hot deformation, Flow stress, Dynamic recrystallization, Segmental constitutive equation

Introduction

The high-speed steel is a kind of steel with special performance, it has good performance and excellent combination of stable hardness and good toughness [1,2]. It is used mostly to manufacture complex thin blade and metal cutting tool, also can be produced high temperature bearing and cold extrusion mould. However, this alloy is rather difficult to deform because of a high content of alloy elements. Its hot workability is sensitive to deformation temperature and strain rate. With the development of the industry, the powder metallurgy (PM) high-speed steel came next. The PM high-speed steel has the advantage of avoiding the mechanical properties degradation and heat treatment deformation caused by alloy elements and carbide segregation.

The hot deformation behaviors and constitutive equation for traditional high-speed steel have been studied [3,4]. But, the PM high-speed steel is relatively less investigated. In the deformation process, constitutive equation as an important part of hot deformation has been researched in a great number of steels and alloys [5-16]. Constitutive equation can be used to describe the relationship of deformation temperature, true strain, strain rate and flow stress. However, the dynamic softening mechanism has a great effect on the flow stress. When building the constitutive equation, the dynamic softening mechanism should be thought about. In this paper, in order to describe dynamic recrystallization, a new dynamic constitutive equation was put forward to study this PM high-speed steel. Based on the thermal simulation of compression under different deformation temperatures and strain rates, we preliminarily studied the peak stress and the corresponding strain, the critical stress and the corresponding strain, and finally established the new dynamic constitutive equation. All of them are benefit for the hot deformation study of the PM highspeed steel.

Experiments

The high-speed steel used in this investigation was produced by hot isostatic press (HIP). The original powder particles are procured by argon atomization, and its diameter range from 20 to 50 μm. The chemical composition (wt,%) is: C, 1.15; Cr, 4.00; V, 3.00; W, 6.00; Mo, 5.00; Fe to balance. The powder was encapsulated in a stainless steel capsule, and then produced by HIP at the temperature of 1100-1150°C and the pressure of 110 MPa for 3 hours. Figure 1 presents the typical microstructure of this PM high-speed steel before hot deformation consisting of a tempered martensite matrix with fine and uniformly distributed carbides.

The cylindrical compression specimens of 8 mm in diameter and 12 mm in height were machined from the as-HIPed billet. Isothermal hot compression tests were conducted on a Gleeble-1500D thermo-simulation machine under the deformation temperatures of 1000, 1050, 1100 and 1150°C, and the constant strain rates were selected as 0.001, 0.01, 0.1 and 1.0 s^-1, respectively. All compression specimens were heated with a rate of 10°C/s and maintained for 3 minutes. The specimens were compressed by 60% of the original height followed by the spray quenching for microstructural observation. The whole processes of heating, heat preservation and hot compression were protected by the argon. After deformation, the grain structures of the deformed specimens were observed by an OLYMPUS-PMG3 optical microscope to analyze the microstructure.

Experimental Results and Discussion

Flow Stress Behavior

Figure 2 shows typical true stress-true strain curves of this PM high-speed steel under different deformation temperatures and strain rates. These curves can be used to show the effect of deformation temperature, strain rate and true strain on the flow stress. Most of the curves exhibited typical characteristics of dynamic recrystallization (DRX) [17]. The flow stress firstly increased to a peak value because of work hardening with the increase of true strain, then decreased and gradually turned to be stable later on. The peak stress appears at the strains range of 0.05-0.10. The strains corresponding to the peak stress increases with the decrease of temperature and the increase of strain rate. Consequently, DRX acts as the main softening mechanism. However, the decrease of temperature and the increase of strain rate will delay the onset of DRX. After the peak stress, the stress decreases with the increase of strain. Under certain conditions, a steady stress state is achieved in which the flow stress remains nearly constant with the increase of strain. Such a flow behavior indicates that the effect of softening mechanisms (DRX, DRV) is sufficiently enough to cancel out the effect of work hardening. This has a good agreement with the observations of other materials, such as super-alloys [18] and titanium alloys [19].

The Relationship of the Peak Stress and the Corresponding Strain

Based on the true stress-true strain curves of this PM high-speed steel, the peak stress and the corresponding strain can be got. The peak stress and the corresponding strain under different deformation temperatures and strain rates are shown in Figures 3 and 4. Based on the experimental results, deformation temperature and strain rate have a great effect on the peak stress and the corresponding strain. Both of them increase with the decrease of temperature and the increase of strain rate. There are two reasons that account for this phenomenon. On the one hand, with the increase of deformation temperature, the thermal activation of material increases, the average kinetic energy of atoms increases, and the critical cutting stress of crystal slip reduces, the blocking effect between the dislocation motion and slip reduces. On the other hand, with the increase of deformation temperature, dynamic softening is more likely to happen. It can reduce the dislocation density and offset the work hardening in the deformation process, thus promote the peak stress and the corresponding strain decrease [20]. Therefore, with the increase of deformation temperature, the peak stress and the corresponding strain decrease gradually. Under a low strain rate, the plastic deformation per unit time is reduced, and there is plenty of time for creep deformation. The reducing of the rate of dislocation proliferation leads to the decrease of dislocation density. The deformation twin, dislocations and other defects decrease in the process of deformation, they will lead to the decreases of the flow stress. At the same time, the extension of the deformation time is benefit for the fully DRX, and it leads to the decrease of the peak stress and the corresponding strain.

According to Sellers [17,18], the relationship among the strain corresponding to the peak stress ε_p, the deformation temperature T and the strain rate ε could be expressed as follows:

ε = a₂ ε^.m1 exp(Q₁ / RT) (1)

Where, Q₁ is the recrystal activation energy; R is the gas constant; and m₁ and a₂ are the constants.

The relationship among the strains corresponding to the peak stress and the critical stress could be expressed as follows:

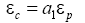(2)

Where, εc is the strains corresponding to the critical stress, a₁ is the constant.

According to the linear regression of the experimental data, it can be obtained that Q₁=86.09 KJ/mol, a₂=2.02 × 10^-5 and m₁=0.08795. Therefore, under the deformation conditions of the temperature range of 1000-1150°C, strain rates between 0.001 s^-1 and 1.0 s^-1, the strain corresponding to the peak stress can be expressed as follows:

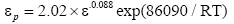(3)

The strain corresponding to the peak stress between simulation and experiment is shown in Figure 5, the error between the calculated value and experimental value is small, and the average value of error is less than 4%. Therefore, this established mathematical model can be used to calculate the strain corresponding to the peak stress under different temperature and different strain rate.

The Activation Energy for Hot Deformation

According to Sellers [21,22], the relationship among the flow stress, the deformation temperature and the strain rate could be expressed by a universal hyperbolic sine function as follows:

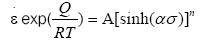(4)

Where, σ is the flow stress; Q is the hot deformation activation energy; A, а and n are the constants.

Zener-Hollomon parameter (Z parameter), known as temperature modified strain rate, was widely used to characterize the combined effect of strain rate and temperature on the deformation process. It can be expressed in the following equation:

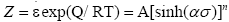(5)

The logarithm of eqn. (4) can be expressed by:

ln ε = ln A + nln[sinh(ασ )] − Q/ RT (6)

Taking partial derivative of both sides of eqn. (6) to strain rate and 1/T, the hot deformation activation energy can be expressed by:

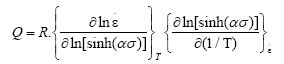(7)

Based on the eqn. (7), the hot deformation activation energy Q can be obtained. Table 1 shows the Q values at different deformation temperatures and strain rates. The results showed that the hot deformation activation energy is greatly affected by deformation temperature and strain rate. The average value of Q is 750.673 KJ/mol under different deformation conditions.

Table 1. The values of hot deformation activation energy Q at different temperatures and strain rates.

Besides, the intrinsic relationship between the deformation activation energy and the thermal-dynamic behavior has been studied. The value of deformation activation energy has a great effect on the microstructure. There is a great difference among the microstructures at different deformation temperatures and strain rates. Figure 6 shows typical deformation microstructures of this PM high speed steel under different deformation temperatures and strain rates. At the same deformation temperature, the deformation activation energy increases with the rising strain rate. Because of the high speed deformation and high deformation activation energy, the dynamical recovery and the dynamical recrystallization are difficult to happen, and the shot residence time under high temperature go against these softening mechanism, Figure 6b and 6c can be used to show this phenomenon in the hot deformation. At the same strain rate, the deformation activation energy decreases with the raising deformation temperature. Besides, the high temperature is beneficial for the dynamical recovery and the dynamical recrystallization. Based on the microstructures, the temperature increase is beneficial for the dynamical recovery and the dynamical recrystallization, as shown in Figure 6c and 6d. The continual dynamical recrystallization and grain growth would take place at a high deformation temperature and a low strain rate, as shown in Figure 6f. In a word, the crushing grains take place fully dynamic recrystallization with the increases of deformation temperature and the decreases of strain rate. As a result, the microstructure is fine and uniform.

The Relationship of the Strain Corresponding to the Peak Stress and the Strain Corresponding to the Critical Stress

The relationship between the strain corresponding to the peak stress and the strain corresponding to the critical stress can be expressed as eqn. (2), the constant of a₁ can be calculated based on the strain corresponding to the peak stress and the strain corresponding to the critical stress at different temperatures and strain rates.

The strain hardening rate at different temperatures and strain rates can be got based on the true stress-true strain curves. The relationship of work hardening rate with strain was obtained by fitting the linear. The strain hardening rate at temperature of 1100°C and strain rate of 0.01 s^-1 is shown in Figure 7. Based on this way, the strain hardening rate at temperature of 1100°C and different strain rates is shown in Figure 8. The strain hardening rate at strain rate of 0.01 s^-1 and different temperatures is shown in Figure 9.

Based on the work hardening rate curve, the strain corresponding to the critical stress under different temperatures and strain rates can be got (shown in Table 2), the strain corresponding to the critical stress decreased with the increase of temperature and the decrease of strain rate. Because, with the increase of deformation temperature and the decrease of strain rate, the mobility of grain boundary increases, and the time of accumulation of distortion energy and dislocation annihilation will delay, which is advantageous to softening mechanism such as the dynamic recrystallization [23].

Table 2. The strain corresponding to the critical stress of powder metallurgy high speed steel at different temperatures and strain rates.

According to the value of the strain corresponding to the peak stress and the strain corresponding to the critical stress, both of them can be fitted by linear (shown in Figure 10), the slop of linear is 0.606, eqn. (1) can be written as:

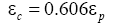(8)

Because the experimental materials is powder metallurgy high speed steel, the grain is small, it is easy for the dynamic recrystallization in the process of thermal simulation of compression, and the strain corresponding to the critical stress is small, the value of a₁ is not big.

Dynamic Recrystallization Constitutive Equation in Different Section

According to the true stress-true strain curves of this PM high speed steel, the dynamic softening mechanism are dynamic recovery and dynamic recrystallization, and the two mechanisms play different leading roles in the different strain range. When the strain reaches a certain value (the critical strain), the stress has a downward trend after reaching a peak stress, the dynamic recrystallization makes a leading role at this time. The dynamic softening mechanism should be fully considered when building a constitutive equation. The dynamic recrystallization constitutive equation in different sectionals can be built, and it is better for predicting the true stress-true strain curves of the PM high speed steel under the different temperatures and strain rates. When the thermal deformation is given priority to with work hardening and dynamic recovery, the relationship between stress and strain can be expressed as [24]:

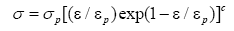(9)

Where, C is a constant.

The logarithm of the eqn. (4) can be shown by a linear relationship, the slope of the linear is the constant C in the eqn. (9). We can choose a number of points on the true stress-true strain curves and fitting these data by using a linear:

c = 0.8739 (10)

The peak stress in the eqn. (4) can be expressed by hot deformation equation:

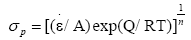(11)

The eqn. (2) can be expressed by another form:

Z = εexp(Q/ RT) = A[sinh(ασ)]ⁿ (12)

Using eqn. (12) in eqn. (6):

(13)

Carrying on linear regression analysis of the peak stresses under different temperatures and strain rates, the value of n, Q and A is determined respectively as n=8.192, Q=750.673 KJ/mol, A=9.6737 × 10⁹. So the peak stress can be expressed as:

(14)

Another expression is:

The eqn. (3) can be expressed by another form:

(15)

When the ε<ε_p, the piecewise constitutive equation can be expressed as:

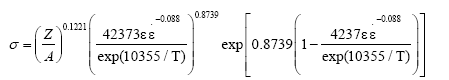(16)

When the ε ≥ p, based on the dynamic recrystallization mechanism, the flow stress after the occurrence of dynamic recrystallization can be described using Arrhenius equation, the piecewise constitutive equation can be expressed as:

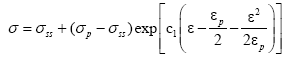(17)

Where, σ_ss is the steady state stress for dynamic recrystallization, C₁ is a coefficient which is associated with the degree of softening and the true stress-true strain curves.

Any point on the true stress-true strain curves before the steady state flow stress can be picked, the strain is εk and the corresponding stress is σ_k (σ_ss<σ_k<σ_p ), the coefficient C₁ can be got by putting the strain and the stress into the eqn. (17):

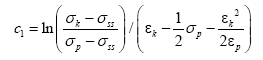(18)

In the process of calculation, the value of εk is 0.6, and the corresponding stress σ_k can be determined. Putting the εk and the σ_k into the eqn. (18), the values of C₁ under every temperature and strain rate can be obtained. In addition, in the process of selecting the value of εk, the value of C₁ is more appropriate when the value of εk is bigger. In the process of calculation, we select the value of εk is near 0.6 in this paper.

It is same as the calculation method of peak stress, the steady state of stress under different temperatures and strain rates can be expressed by hot deformation equation:

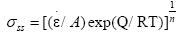(19)

By regression, the value of n is determined as n=5.1027, and the value of corresponding activation energy for the steady state stress is determined as Q=466.361 kJ/mol. The value of A depends on the temperature and the strain rate, the value of A under different conditions can be obtained by regression. So the eqn. (14) can be written as:

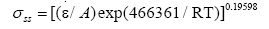(20)

The value of steady stress under a certain temperature and strain rate can be calculated by the above formula. Using eqns. (14), (15) and (20) and C₁ in eqn. (17), the constitutive equation can be obtained when ε ≥ ε_p.

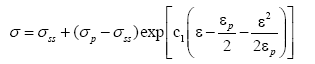(21)

Validation of the experimental model: the flow stresses under different temperature and strain rate can be obtained by the above sectional constitutive equation. Taking the strain rate of 0.01 s–1 for example, the comparison between the calculated values and experimental values can be obtained. The result is shown in Figure 11.

By the validation, the dynamic recrystallization constitutive equation with subsection coincide well with the experimental value, the average error is about 3.4%, especially under high temperature, the calculated flow stresses are more coincident with the results of experiments. Under a same deformation temperature, the values of error decrease gradually with the increase of the strain. The experimental value and calculated value is almost consistent after the strain reaches a certain value. Therefore, the dynamic recrystallization constitutive equation got in this paper can be used to predict the flow stress very well under the high strain.

Conclusion

1. The flow stress of this PM high-speed steel is influenced by strain during hot deformation. Because work hardening makes a main role in the initial stage (ε<0.1), the flow stress increases sharply and reaches peak quickly; The effect of dynamic softening is greater than the effect of work hardening with the continued increase of strain, and the flow stress gradually decreases, the flow stress tends to be stable with the further increase of strain. The flow stress decreases with increase of the deformation temperature or decrease of the strain rate.

2. The peak flow stress and the corresponding strain are strikingly influenced by deformation temperature and strain rate during hot deformation. Both of them decrease with increase of the deformation temperature or decrease of the strain rate. The mathematical model of the strain corresponding to the peak stress under different strain rate and deformation temperature is established as:

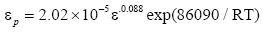
3. The strain hardening rate is extremely different in different deformation stages in the process of deformation. The strain hardening rate decreases sharply in the initial stage of deformation. When the strain reaches the critical strain, the speed of strain hardening rate reduction is slow, and the strain hardening rate reaches a negative value. The strain hardening rate increases gradually and gradually tends to zero with the further increase of strain, so the flow stress reaches a steady state. The relationship between the strain corresponding to the peak stress and the strain corresponding to the critical stress can be described as: εc=0.606 ε_p.

4. The softening mechanism of dynamic recrystallization should be considered in the hot deformation, and the dynamic recrystallization constitutive equation in different sectional for the PM high speed steel are established as:

When ε<ε_p:

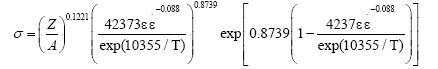
When ε ≥ ε_p:

Acknowledgement

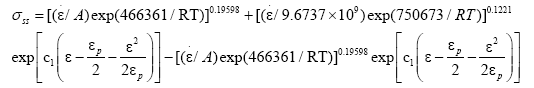
The work was supported by Natural Science Foundation of China (Grant No. 51775440), the National Natural Foundation of China (Grant No. 51175431) and China Postdoctoral Science Foundation (Grant No. 2012T50818).

References

1. Babul T, et al. Nitro-oxidation of tools manufactured from high-speed steel. Mater Manuf Process 2009;24:842-846.
2. Chaus AS. Microstructural and properties evaluation of M2 high speed steel after inoculating addition of powder W and WC. Mater Sci Techlond 2014;30:1105-1115.
3. Zhou B, et al. Breakdown Behavior of Eutectic Carbide in High Speed Steel During Hot Compression. J Iron Steel Res Int 2011;18:41-48.
4. Yang J, et al. Effect of Rare Earth on Microstructures and Properties of High Speed Steel With High Carbon Content. J Iron Steel Res Int 2007;14:47-52.
5. Chai RX, et al. Prediction of constitutive behaviour of 20CrMnTiH steel under hot deformation conditions. Mater Sci Technol 2012;28:857-863.
6. Guo B, et al. Constitutive Equations for Flow Behavior of Powder-forged Fe-0.5C-2Cu Steel under Hot Compression. J Iron Steel Res Int 2014;21:389-395.
7. Peng P, et al. Hot Deformation Behavior of a New 9%Cr Heat Resistant Steel G115. J Iron Steel Res 2013;20:73-79.
8. Tian L, et al. Effect of austenitic state on microstructure and mechanical properties of martensite/bainite steel. J Mater Res 2014;29:887-895.
9. Zhong J, et al. Constitutive modelling for high temperature behaviour of 12CrNiMoWV martensitic stainless steel. Mater Sci Technol 2012;28:719-726.
10. Guo B, et al. Flow Behavior and Numerical Simulation of Spray-Formed FGH95 Superalloy Under Hot Compression. J Iron Steel Res Int 2013;20:69-74.
11. Matlock DK and Speer JG. Processing opportunities for new advanced high-strength sheet steels. Mater Manuf Process 2010;25:7-13.
12. Yan T, et al. Modeling of Hot Deformation Behavior of 55SiMnMo Medium-Carbon Steel. J Iron Steel Res 2013;20:125-130.
13. Sun Y, et al. Modeling the Constitutive Relationship of Powder Metallurgy Ti-47Al-2Nb-2Cr Alloy During Hot Deformation. J Mater Eng Perform 2015;24:1313-1321.
14. Wang MH, et al. Quantitative analysis of work hardening and dynamic softening behavior of low carbon alloy steel based on the flow stress. Mater Design 2013;45: 384-392.
15. Yu JL, et al. A theoretical and experimental study on the constitutive model of aluminium foams. Mater Sci Forum 2010;638-642:1878-1883.
16. Bush AA, et al. Electrical properties of ceramic samples of (1–x)Ba(Ti1–yZry)O₃ ∙ xPbTiO₃ solid solutions. Inorg Mater 2017;53:318-325.
17. Xu Y, et al. Dynamic recrystallization kinetics model of X70 pipeline steel. Mater Des 2012;39:168-174.
18. Ning YQ, et al. Hot deformation behavior of Ti–5.0 Al–2.40 Sn–2.02 Zr–3.86 Mo–3.91 Cr alloy with an initial lamellar microstructure in the α+ β phase field. Mater Sci Eng A 2011;528:1812-1818.
19. Li H, et al. Flow behavior and processing map of PM Ti–47Al–2Cr–0.2 Mo alloy. Trans Nonfer Metal Soci China 2012;22:754-760.
20. Briottet L, et al. A mechanical interpretation of the activation energy of high temperature deformation in two phase materials. Acta Mater 1996;44:1665-1678.
21. Richardson GJ, et al. Recrystallization during creep of Nickel. Acta Metal 1996;14:1225-1236.
22. Jonas JJ, et al. Strength and structure under hot-working conditions. Metall Rev 1969;14:1-24.
23. Prasad YVRK, et al. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242. Metall Mater Trans A 1984;15A:1883-1892.
24. Laasraou A and Jonas JJ. Prediction of steel flow stresses at high temperatures and strain rates. Metall Mater Trans A 1991;22 A:1545-1558.