Department of Mathematics, Narayana Educational Institutions, Bangalore, India
Received date: 08/07/2016; Accepted date: 22/08/2016; Published date: 26/08/2016
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
The aim of this note is to prove some well-known results related to the Fermat-Torricelli point in a new prominent way.
First Fermat point, Fermat lines
The Fermat point is named for the point which is the solution to a geometric challenge that Pierre Fermat posed for Evangelista Torricelli, who was briefly an associate of the aged Galileo. Fermat challenged Torricelli to find the point P in an acute triangle ABC which would minimize the sum of the distances to the vertices A, B, and C. The triangle need not actually be acute, but if the largest angle reaches 120 degrees or more, then the vertex at the largest angle is the solution. For a general solution, one approach is to construct equilateral triangles on each side of the triangle (actually only two are needed) and draw the segments connecting the opposite vertices of the original triangle and the newly created equilateral vertices. They intersect in a point which is the solution. The point is called the Fermat point. The more details about this point and its generalizations is in [1-4].
In this note we will try to establish the very fundamental results related to this point.
Notations:
Let ABC be a triangle. We denote its side-lengths by a, b, c, its semi perimeter by 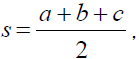 its area by Δ , its Circumradius by
its area by Δ , its Circumradius by 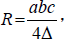 In radius by
In radius by 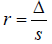
Let us define S2 , S2 and S3 as described below:
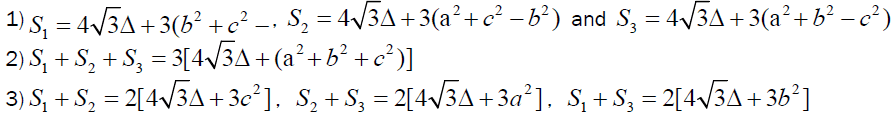
Some Basic Lemma’s:
Lemma -1
If S1, S2 and S3 are described as mentioned above then 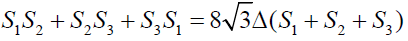
Proof:
Clearly 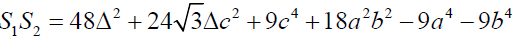
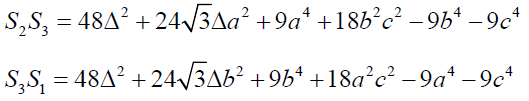
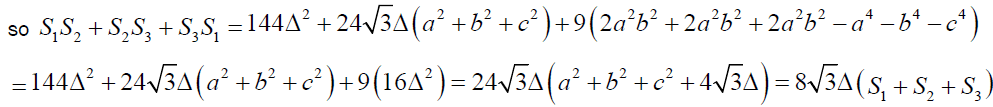
Hence proved.
Lemma -2
If S1, S2 and S3 are described as mentioned above then,
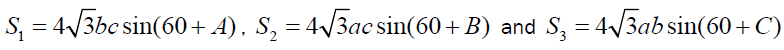
Proof:
We have sin(60+A) = sin60 cos A + sin A cos 60 = 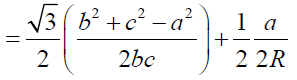
It implies sin(60+A) 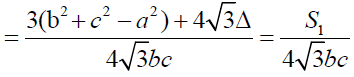
Further simplification gives required conclusions.
Theorem-1
If Triangle ABC is an arbitrary triangle (whose all angles are less than 120 degrees) let the triangles A1BC, B1CA and C1AB are equilateral triangles constructed outwardly on the sides BC, CA and AB of triangle ABC then AA1, BB1 and CC1 are concurrent and the point of concurrence is called as First Fermat Torricelli Point(T1) or Outer Fermat Torricelli Point (T1 ) .
Proof:
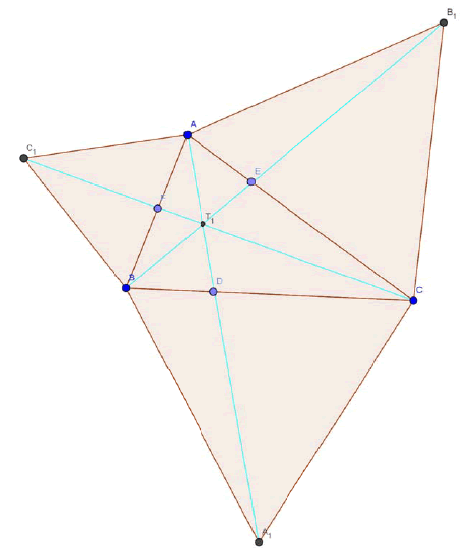
Let D, E and F are the point of intersections of the lines AA1, BB1 and CC1 with the sides BC, CA and AB.
Now clearly by angle chasing and using the fact “cevian divides the triangle into two triangles whose ratio between the areas is equal to the ratio between the corresponding bases.”
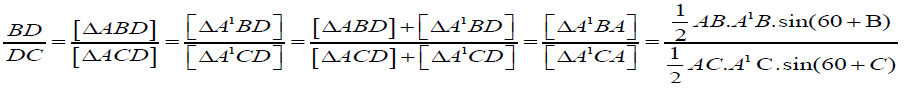
It implies 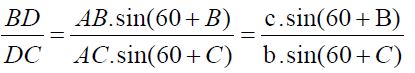
And we have 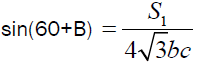
Hence 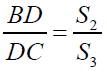
Similarly 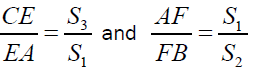
Now by the converse of Ceva’s theorem,
Since 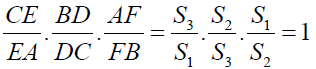
The lines AA1, BB1 and CC1 are concurrent and the point of concurrence is called as First Fermat Point (T1).
Theorem-2
Triangles A1BC, B1CA and C1AB are equilateral triangles constructed outwardly on the sides BC, CA and AB of triangle ABC then AA1, BB1 and CC1 are equal in length. (For the recognition sake let us call the lines AA1, BB1 and CC1 as Fermat Lines) [5].
Proof:
Clearly from triangle ABA1,
By cosine rule 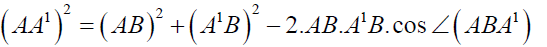
It implies 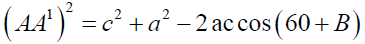
It further gives 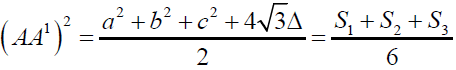
Similarly we can prove that 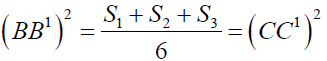
Hence 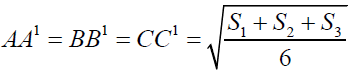
Theorem-3
Let D, E and F are the point of intersections of the lines AA1, BB1 and CC1 with the sides BC, CA , AB respectively and if T1 is the First Fermat Point then
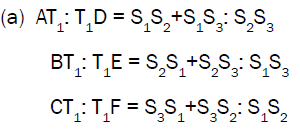
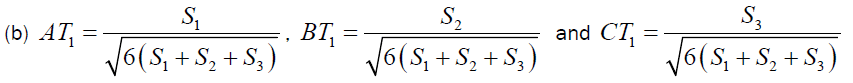
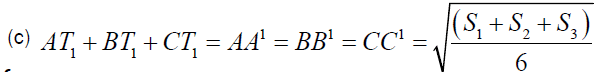
Proof:
Clearly we have, 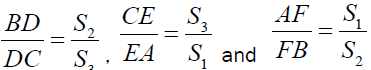
Now from triangle ABT, the line BT1E is acts as transversal so by Menelaus theorem we have:
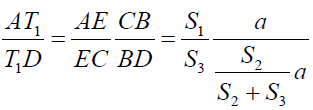
It implies 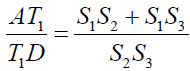
Similarly we can prove that 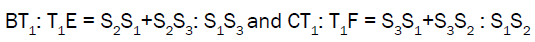
Hence the conclusion (a) follows:
Now from conclusion (a) we have 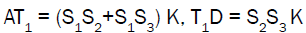 for some constant K
for some constant K
It follows that 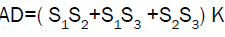
And clearly 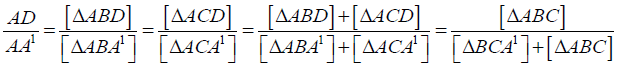
It gives that 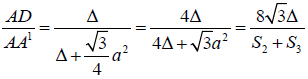
So 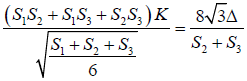
Using the above relation and lemma-1 we can find the proportionality constant K and by replacing the value of K in AT1 = (S1S2+S1S3) K we can arrive at the required conclusion (b).
Now using (b) we can prove the conclusion (c).
Theorem-4
Triangles A1BC, B1CA and C1AB are equilateral triangles constructed outwardly on the sides BC, CA and AB of triangle ABC then the circumcircles of the Triangles A1BC, B1CA and C1AB conccur at T1.
Proof:
We need to prove that set of the points 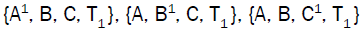 are concyclic.
are concyclic.
So it is enough to prove that by ptolemy’s theorem 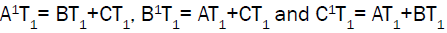
Clearly 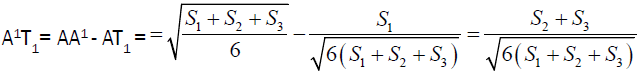
It implies that A1T1= BT1+CT1
Similarly we can prove the remaining two relations.
Corollary:
If T1 is the First Fermat point of triangle ABC then
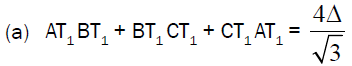
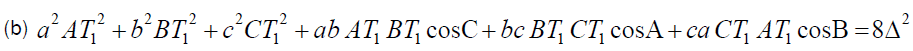
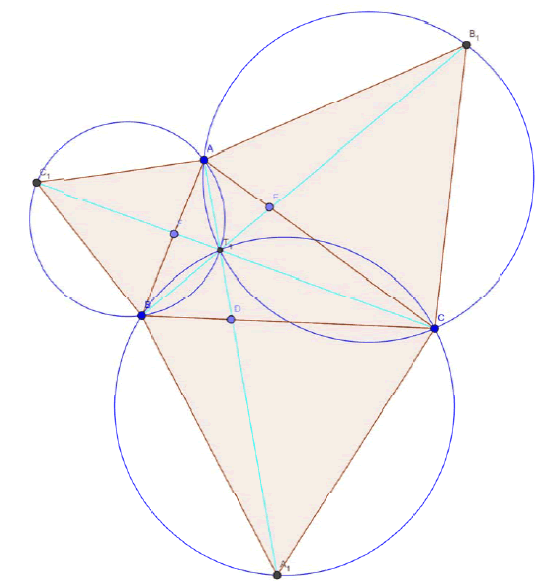
Proof:
For (a),
Clearly by Theorem-4 we have angle AT1B = angle BT1C = angle CT1A = 1200
So 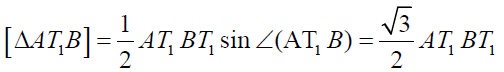 (p)
(p)
Similarly 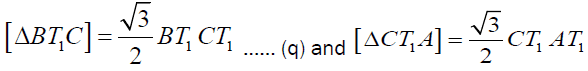 (r)
(r)
Now using the fact 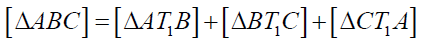 and (p), (q) and (r) we can prove conclusion (a).In the
alternative manner,
and (p), (q) and (r) we can prove conclusion (a).In the
alternative manner,
Using theorem – 3, lemma-1 and by little algebra we can prove the conclusion (a).
Now for (b),
Clearly by Theorem – 4 and by applying cosine rule for the triangles AT1B, BT1C and CT1A we can prove that
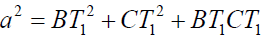 (x)
(x)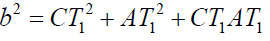 (y)
(y)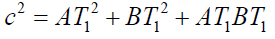 (z)
(z)Now consider
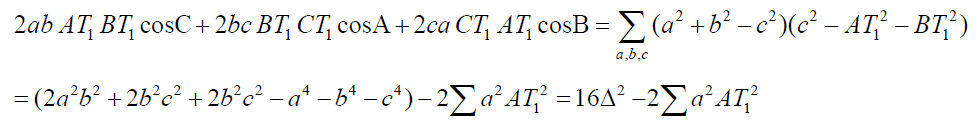
Equivalently,
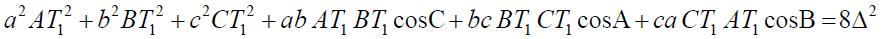
This finishes proof of conclusion (b).
When one of the angles of the triangle is 120° or greater, then the Fermat point (which still exists) is no longer the point that minimizes the sum of the distances to the vertices, but the minimal point is located at the vertex of the obtuse angle. Clearly Theorem-3 derives this fact.
The author is grateful to the creators of the free Geogebra software, without which this work would have been impossible and the author is would like to thank an anonymous referee for his/her kind comments and suggestions, which lead to a better presentation of this paper.