Keywords
|
| Direct integration of ultra-capacitors, dual inverter, energy storage interfacing, and non-integer voltage ratio. |
INTRODUCTION
|
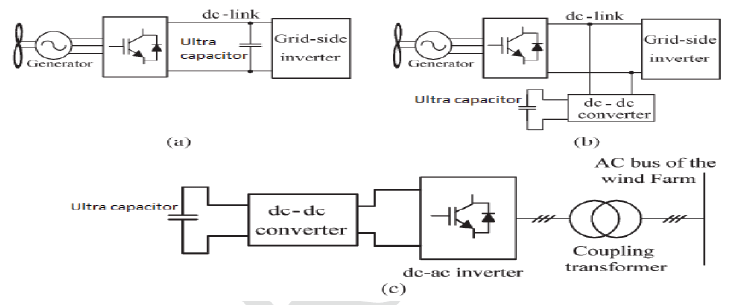
| Global warming, one of the most critical environmental problems arising in the world, must be taken into consideration. In an attempt to prevent the realization of these fears, we know that utilization of renewable energy has become very useful in the emissions of greenhouse effect gases (CO2, NOx, SOx , etc.). However, the generated power is always fluctuated due to an environmental status. In order to promote renewable energy and compensate the fluctuating power, though an energy storage system is effective, one must resolve a number of issues, including those related to efficiency, economy and environment. In recent years, Short-Term power exchange exploitation ultracapacitors is actively pursued in wind generation systems as evident from the massive variety of techniques according within the literature. These techniques may be divided into 2 major classes, looking on the means that ultra-capacitors square measure connected to the wind generation system. within the initial class, the ultra-capacitors square measure connected to the intermediate dc link of the consecutive convertor system as shown in Fig. 1(a) and (b). Despite the fact that the direct affiliation shown in Fig. 1(a) is that the simplest, it might be troublesome to urge the most use of the ultra-capacitor bank thanks to dc-link voltage limitations obligatory by the grid-side electrical converter. The effects of this issue will otherwise be reduced if associate degree intermediate dc–dc convertor is placed between the ultra capacitor and also the dc link as shown in Fig.1 (b) [10], [11]. This dc–dc converter has to possess two-way power flow capability and therefore needs a minimum of 2 quick change devices rated to the peak power. Moreover, the low-pass filter (LPF), comprising an inductor and a capacitor, degrades the dynamic response [12]. Therefore, the interfacing dc– dc converter increases the system cost, power losses, and complexity. In the second category, the common ac bus is used for power exchange, as shown in Fig. 1(c), and it requires an additional dc–dc converter, a dc–ac inverter, and a coupling transformer [13]. Therefore, in both cases, these additional converters essentially increase the overall cost and power losses, which would be absent if a direct integration scheme with full controllability is available. |
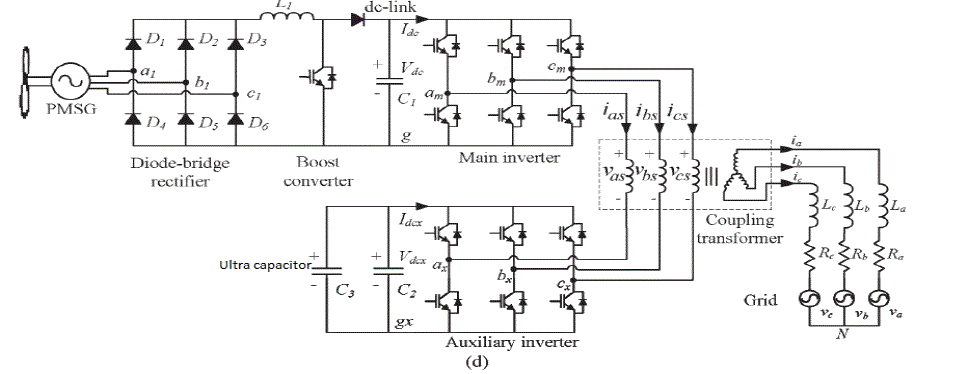
| This paper therefore presents a direct integration scheme for ultra capacitors with the use of the grid-side inverter. The proposed inverter system is shown in Fig. 1(d), and it is formed by cascading two two-level inverters through a coupling transformer. The two inverters are named as the main inverter and the auxiliary inverter. The ultra capacitor bank is directly connected across the dc link of the auxiliary inverter. The dynamic behavior of the ultra capacitor voltage is handled by the inverter controller, eliminating the need for an additional boost converter. The main inverter is a high-power low-speed inverter which operates at fundamental frequency, producing square wave outputs. Harmonics produced by the square wave output are compensated by the low-power high-speed auxiliary inverter. As the highpower main inverter operates at the fundamental frequency, it can be constructed using devices like gate turn-off thyristors (GTOs), emitter turn-off thyristors (ETOs), or integrated gate-commutated thyristors (IGCTs).On the other hand, the auxiliary inverter can be constructed using more commonly available devices like insulated gate bipolar transistors (IGBTs). This particular power and frequency splitting arrangement helps to reduce power losses in the inverter system [14], [15]. |
ANALYSIS ON ULTRA CAPACITOR CHARGINGAND DISCHARGING PROCESS
|
| In the proposed system, the dc-link voltages of both the main inverter and the auxiliary inverter are allowed to vary independently and dynamically. |
 |
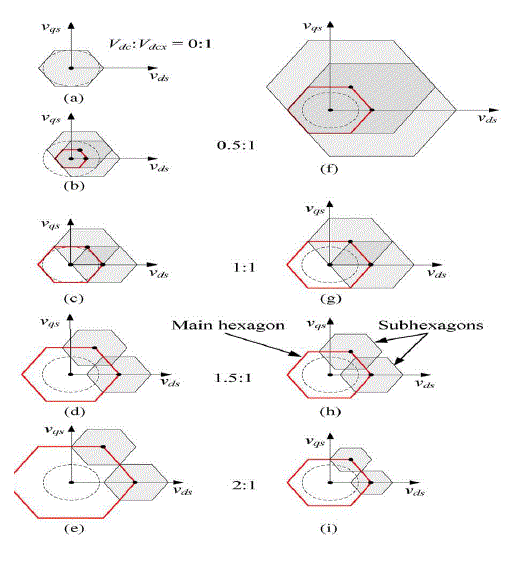
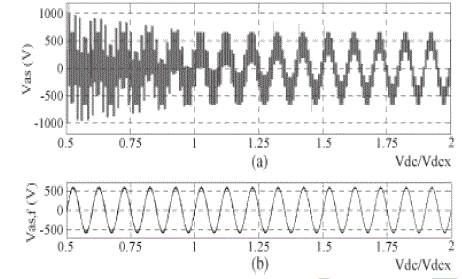
| As a result, the space vector diagram of the combined inverter takes different shapes at different dc-link voltage ratios as shown in Fig.2. Here in Fig. 2, hexagons formed by the voltage vectors of the main inverter are named as main hexagons while the hexagons formed by auxiliary inverter vectors are named as sub hexagons. This vector representation explains the operations of the main inverter and auxiliary inverter. |
POWER SHARING MPPT AND GENERATOR-SIDE CONTROLLER
|
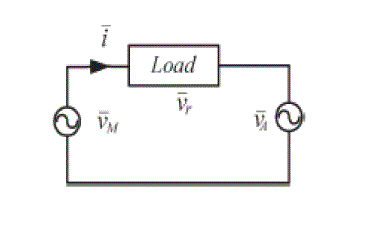
| The output voltage vector Vr is combination of main inverter voltage and auxiliary inverter voltage. The following mathematical equations gives the power, voltage equations of the grid, main inverter and auxiliary inverter. The equivalent circuit of the proposed system is shown in Fig. 5.The circuit describes the output voltage vector (Vr), main inverter voltage vector (VM), auxiliary inverter voltage vector (VA), and the current vector (i). The output voltage vector is combined output of the main inverter voltage vector and the auxiliary inverter voltage vector as in Eq. (1). The real power delivered to the load can be expressed as the dot product in Eq. (2). Furthermore, the output power is equivalent to the sum of the main inverter power and the auxiliary inverter power as expressed in Eq. (3). Eq. (4) and Eq. (5) show the relationships between inverter voltage vectors and corresponding switching states. With the help of these five equations, an expression can be derived for the power of the auxiliary inverter, i.e., the supercapacitor power, as in Eq. (6). where VM, PM, and SiM (i = 1, 2, 3) represent the main inverter voltage, power, and switching function while those of the auxiliary inverter are given by Vr, PM, and SiA(i = 1, 2, 3), respectively. Vr represents the output voltage, and Pgrid represents the real power flow to the grid. |
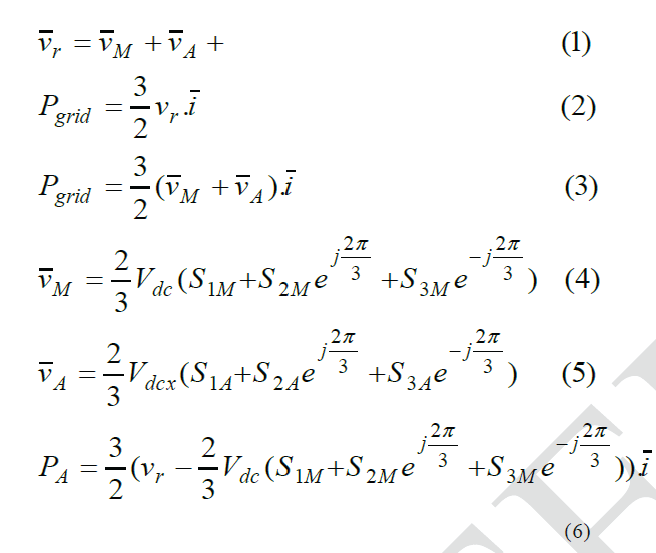 |
| According to (6), it can be deduced that, for a given output power, supercapacitor power varies with the main inverter dc-link voltage Vdc. Therefore, super capacitor power can be controlled by controlling the main inverter dc-link voltage. Furthermore, according to (3), for a given output power, the main inverter power solely depends on the auxiliary inverter power. |
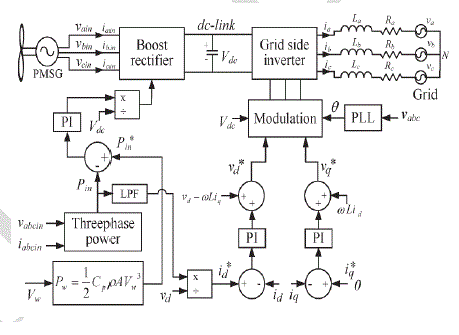
| Therefore, the maximum power point of the wind turbine can indirectly be tracked by changing the main inverter dc-link voltage. The usual practice is to maintain this voltage at a constant level with the help of a controlled rectifier or a boost rectifier placed between the main inverter and the wind turbine generator (WTG) system. However, in the proposed system, the boost rectifier is used to vary the main inverter dc-link voltage and thus indirectly track the maximum power point of the WTG. The controller block diagram for this indirect maximum power point tracking (MPPT) is shown in Fig. 6. In this controller, the measured wind speed and the parameters of the turbine model are used to derive a power reference for the generator-side converter. The actual generator power is compared with the reference, and the error is fed into a proportional–integral (PI) controller which generates a voltage reference for the boost rectifier. This voltage reference is normalized to produce the modulation index for the boost rectifier. |
DESIGN OF THE GRID-SIDE INVERTER
|
| In the proposed system, the main inverter is operated in the six-step mode, which moves slowly from one vector to the next. This generates square wave outputs from the main inverter which get smoothened by the auxiliary inverter. Owing to this low-frequency operation, the main inverter switching losses get reduced [14], [15]. The auxiliary inverter, which acts as an active filter, is operated at high switching frequency by utilizing a space vector modulation (SVM) method. Therefore, the overall modulation is a combination of the six-step mode and SVM [16] and [17]. The grid-side inverter controller employs an inner current controller and an outer power controller as shown in Fig. 6. The grid voltage and current injected into the grid are converted into the synchronous reference frame. The direct component of the inverter output current id controls the active power exchange with the grid while the quadrature component iq controls the reactive power. Therefore, to generate a reference for the direct current component, the instantaneous active power of the generator-side converter is passed through an LPF [6]. The quadrature current reference I*q is set to zero to keep the power factor at the grid connection point at unity. These active and reactive current references (I*d and I*q) are then compared with actual current components, and the errors are passed through PI controllers to produce voltage references v*d and v*q, respectively. Eq. (7) and Eq. (8) are then used to calculate the amplitude and angle of the reference voltage vector. In Eq. (8), θ is the initial phase angle of the reference vector. |
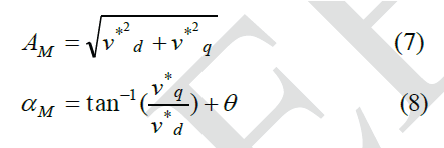 |
DESIGN OF ULTRA CAPACITOR AND GENERATOR-SIDE CONTROLLER
|
| The main cause of power fluctuations is the change of wind speed. Therefore, the capacity of the energy storage system is also a function of the wind speed variation. In order to analyze this relationship, the wind is modelled as the sum of a dc quantity and a series of harmonics as in Eq. (9) [18]. In the following simulation, the wind speed fluctuation is assumed to be 20% of the mean value as in Eq. (10). The power captured from the wind can be expressed as in Eq. (11). |
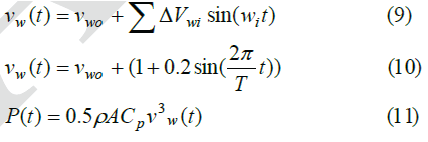 |
| Where Vw is the instantaneous wind speed, Vw0 is the mean wind speed, ΔVwi is the harmonic amplitude, ωi is the angular frequency (f = 1/T = ω/2π = 0.1 ∼ 10 Hz), ρ is the density of air, A is the swept area of wind turbine blades, and Cp is the coefficient of power conversion. Power fluctuations caused by the aforementioned wind speed change have to be compensated by the energy storage system. |
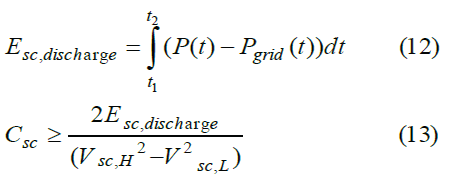 |
| Therefore, the required capacity of the supercapacitor bank is determined according to where Esc, discharge is the amount of energy taken out from the supercapacitor during the discharging period, t1 and t2 are the starting time and end time of the discharging period, respectively, and Vsc, H and Vsc, L are the starting and end values of the super capacitor voltage. Super capacitors behave as resistors at high frequencies (typically beyond few tens of hertz) [19], [20]. Therefore, the proposed system requires an electrolytic capacitor to assist supercapacitors at high frequencies. |
SIMULATION RESULTS
|
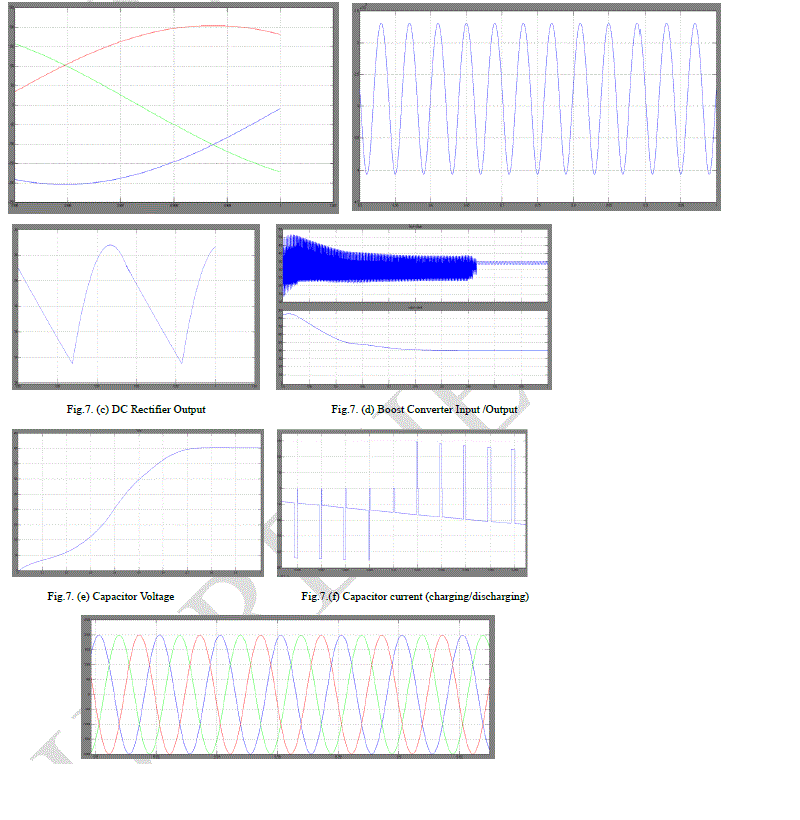
| The proposed direct integration scheme has been tested using computer simulations on MATLAB/SIMULINK digital simulation platform. The schematic diagram of the simulation setup is shown in Fig. 1(d). The wind speed profile shown in Fig. 7(a) with an average speed of 10 m/s, 20% harmonic amplitude, and 1-Hz harmonic frequency is used to test the performance of the proposed system and control strategy. The Proposed system is evaluated in matlab Simulink software using the Table I parameter values. |
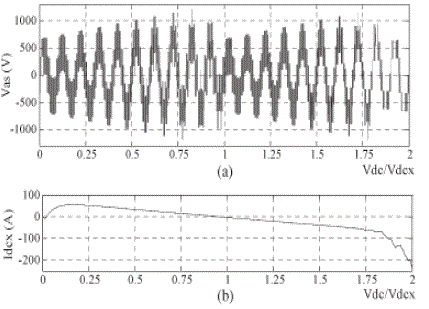
| The corresponding variations of generator output is shown in Fig.7(a). The input power shows a large variation ranging to 200 kW. The average value of the output power is 200 kW with a small variation of ïÃâñ5kW. A simple calculation would reveal that the corresponding input power fluctuation is about 66% while the output power fluctuation is less than 8.4%. This proves the efficiency of the proposed system in mitigating power fluctuations caused by wind changes. As mentioned in Section III, the main inverter dc-link voltage is changed to control the ultra capacitor power and thus to indirectly track the MPPT of the WTG. The corresponding main inverter dc-link voltage and the supercapacitor voltage variations are shown in Fig. 7(e). According to this diagram, the main inverter dc-link voltage shows a large variation ranging from 400 to 1200 V which is far below the upper limit of modern IGCT devices, and therefore, the proposed system is feasible. Similarly, the supercapacitor voltage varies with a maximum of Vsc, H = 800 V and a minimum of Vsc, L = 400 V. Therefore, according to (12) and (13), the required minimum capacitance of the supercapacitor bank is found to be 43.75 mF which is a realistic value. The boost converter input and outputs are shown in Fig.7. (d). the main inverter dc-link current is nearly constant due to the six-step operation of the main inverter. However, the supercapacitor current varies with the main inverter dc-link voltage owing to the pulse width modulation (PWM) operation of the auxiliary inverter. The change of the modulation index of the generator-side converter (boost rectifier) for the aforementioned wind speed profile is shown in Fig. 7 (b). The corresponding generator currents are shown in Fig. 7 (a). Similarly, the variations of the amplitude and power angle of the grid-side inverter output voltage are shown in Fig. 7 (c) and (d), respectively. These two values are nearly constant owing to the smooth power delivery to the grid. Consequently, the d–q-axis currents of the grid side inverter are nearly constant as shown in Fig.7 (e). And the capacitor current charging and discharging is shown in Fig. 7. (f) The corresponding three phase currents of the grid-side inverter and their zoomed-in view are shown in Fig.7 (g). |
CONCLUSION
|
| The direct integration of energy storage devices has a number of advantages such as reduction in power losses, cost, and complexity. Therefore, in this paper, the popular dual inverter topology was customized to connect a supercapacitor bank directly into the dc link of the auxiliary inverter. The operation of the proposed system was discussed in detail. Simulation and experimental results were presented to verify the efficiency of the proposed system in suppressing short-term wind power fluctuations. |
Tables at a glance
|
 |
| Table 1 |
|
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
 |
 |
 |
| Figure 5 |
Figure 6 |
Figure 7 |
|
References
|
- T. Kinjo, T. Senjyu, N. Urasaki, and H. Fujita, “Output leveling of renewable energy by electric double-layer capacitor applied for energy storage system,” IEEE Trans. Energy Convers., vol. 21, no. 1, pp. 221–227, Mar. 2006.
- E. Naswali, C. Alexander, H. Y. Han, D. Naviaux, A. Bistrika, A. Jouanne, A. Yokochi, and T. K. A. Brekken, “Supercapacitor energy storage for wind energy integration,” in Proc. ECCE, Sep. 17–21, 2011, pp. 298–305
- L. Qu and W. Qiao, “Constant power control of DFIG wind turbines with supercapacitor energy storage,” IEEE Trans. Ind. Appl., vol. 47, no. 1, pp. 359–367, Jan./Feb. 2011.
- N. Bingchang and C. Sourkounis, “Energy yield and power fluctuation of different control methods for wind energy converters,” IEEE Trans. Ind. Appl., vol. 47, no. 3, pp. 1480–1486, May/Jun. 2011.
- M.S. Lu, C. L. Chang, W.J. Lee, and L. Wang, “Combining the wind power generation system with energy storage equipment,” IEEE Trans. Ind. Appl., vol. 45, no. 6, pp. 2109–2115, Nov./Dec. 2009.
- S. M. Muyeen, R. Takahashi, T. Murata, and J. Tamura, “Integration of an energy capacitor system with a variable-speed wind generator,”IEEE Trans. Energy Convers., vol. 24, no. 3, pp. 740–749, Sep. 2009.
- Li.Wei, G. Joos, and J. Belanger, “Real-time simulation of a wind turbine generator coupled with a battery supercapacitor energy storage system,” IEEE Trans. Ind. Electron., vol. 57, no. 4, pp. 1137–1145, Apr. 2010.
- G. Guidi, T. M. Undeland, and Y. Hori “An optimized converter for battery-supercapacitor interface,” in Proc. IEEE Power Electron. Spec. Conf., Jun. 2007, pp. 2976–2981.
- C. Abbey and G. Joos, “Supercapacitor energy storage for wind energy applications,” IEEE Trans. Ind. Appl., vol. 43, no. 3, pp. 769–776, May/Jun. 2007.
- L. Allegre, A. Bouscayrol, and R. Trigui, “Influence of control strategies on battery/supercapacitor hybrid energy storage systems for traction applications,” in Proc. IEEE Veh. Power Propulsion Conf., Sep. 2009, pp. 213–220.
- Abedini and A. Nasiri, “Applications of super capacitors for PMSG wind turbine power smoothing,” in Proc. IEEE Ind. Electron. Conf., Nov. 2008,pp. 3347–3351.
- K. Jin, M. Yang, X.-B. Ruan, and M. Xu, “Three-level bidirectional converter for fuel-cell/battery hybrid power system,” IEEE Trans. Ind. Electron., vol. 57, no. 6, pp. 1976–1986, Jun. 2010.
- L. Wei and G. Joos, “Comparison of energy storage system technologies and configurations in a wind farm,” in Proc. IEEE Power Electron. Spec. Conf., Jun. 2007, pp. 1280–1285.
- K. A. Corzine, W. Wielebsk, F. Z. Peng, and J. Wang, “Control of cascaded multilevel inverters,” IEEE Trans. Power Electron., vol. 19, no. 3, pp. 732–738, May 2004.
- S. Lu and K. A. Corzine, “Advanced control and analysis of cascaded multilevel converters based on P-Q compensation,” IEEE Trans. Power Electron., vol. 22, no. 4, pp. 1242–1252, Jul. 2007
- S. D. G. Jayasinghe, D. M. Vilathgamuwa, and U. K. Madawala, “Direct integration of battery energy storage systems in distributed power generation,” IEEE Trans. Energy Convers., vol. 26, no. 2, pp. 677–685, Jun. 2011.
|