Keywords
|
| MIMO, OFDM, ZF, MMSE, ML, Constant Modulus Algorithm(CMA),Rayleigh fading channel. |
INTRODUCTION
|
| Multiple Input Multiple Output(MIMO) systems have been recently emerged as a key technology in wireless communication systems for increasing both data rates and performance. MIMO is an antenna technology that used both in transmitter and receiver equipment for wireless radio communication. MIMO uses multiple antennas to send multiple parallel signals for transmission. Wireless communication technology has shown that when multiple antennas at both transmitter and receiver are employed it provides the possibility of higher data rates compared to single antenna systems [1][2]. MIMO exploits the space dimension to improve wireless system capacity, range and reliability. In the never ending search for increased capacity in a wireless communication channel it has been shown that by using MIMO OFDM systems[3] it is possible to increase that capacity substantially. Especially in broadband application where Inter-symbol Interference is a critical factor. Equalizers are employed to reduce such interference. MIMO system transmits differentsignals from each transmit element so that the receiving antenna array receives a superposition of all the transmitted signals. MIMO has eminent features which offer significant increment in data throughput and link range without additional bandwidth and increase transmit power. Modern wireless communication standards such asIEEE 802.11n (Wi-Fi), 4G, 3GPP Long Term Evolution (LTE) and WiMAX has become an important part due to these properties [4-5]. |
| Orthogonal frequency division multiplexing (OFDM) reduces receiver complexity in wireless broadband systems. The use of MIMO technology in combination with OFDM therefore seems an attractive solution for future wireless communication. In OFDM, one user is dedicated to a particular time slot to access all the sub carriers and all carriers are transmitted in parallel with same amplitude i.e. in OFDM, the user device can transmit using the entire carrier at a time. Orthogonal Frequency Division Multiplexing is a multicarrier modulation technique in which FFT space is divided into orthogonal sub-carriers. In this technique, the whole transmission bandwidth is split into many closely spaced narrow sub-channels until overlapped and are transmitted in parallel. Each sub-channel is narrow enough so that it experiences a flat fading although the overall radio propagation environment is frequency selective. |
| In MIMO wireless communication multipath fading is usual phenomenon that causes ISI from the transmitted signal. To remove ISI[6] from transmitted signal, BER reduction is compulsory. In this paper different equalization approach called Zero Forcing(ZF), Minimum Mean Square error (MMSE), Maximum Likelihood (ML) and Constant Modulus Algorithm (CMA) equalizers has been discussed. The channel is a Rayleigh fading channel and the modulation as QPSK has been taken. In this Paper, we used 4×4 perfect codes i.e number of transmit antenna is 4 and number of receiver antenna is 4. |
II.CONSIDERED CHANNELS IN PROPOSED MODEL
|
a. Additive White Gaussian Channels.
|
| In telecommunication, inter symbol interference(ISI) is a form of distortion of a signal in which one Symbol interferes with subsequent symbols. This is an unwanted phenomenon as the previous symbols have similar effect as noise, thus making the communication less reliable. ISI usually caused by multipath propagation or the inherent non-linear frequency response of a channel causing successive symbols to "blur" together. The presence of ISI in the system introduces errors in the decision device at the receiver output. Therefore, in the design of the transmitting and receiving filters, the objective is to minimize the effects of ISI, and thereby deliver the digital data to its destination with the smallest error rate possible. Ways to fight inter symbol interference include adaptive equalization and error correcting codes. |
b. Rayleigh Fading Channel.
|
| Rayleigh fading models assume that the magnitude of a signal that has passed through such a transmission medium will vary randomly, or fade, according to a Rayleigh distribution the radial component of the sum of two uncorrelated Gaussian random variables. Rayleigh fading is a reasonable model when there are many objects in the environment that scatter the radio signal before it arrives at the receiver. The central limit theorem holds that, if there is sufficiently much scatter, the channel impulse response will be well modeled as a Gaussian process irrespective of the distribution of the individual components. |
| If there is no dominant component to the scatter, then such a process will have zero mean and phase evenly distributed between 0 and 2π radians. The envelope of the channel response will therefore be Rayleigh distributed. Calling this random variable R, it will have a probability density function: |
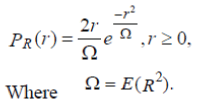 |
| Often, the gain and phase elements of a channel's distortion are conveniently represented as a complex number. In this case, Rayleigh fading is exhibited by the assumption that the real and imaginary parts of the response are modeled by independent and identically distributed zero-mean Gaussian processes so that the amplitude of the response is the sum of two such processes. |
III. EQUALIZER
|
| Equalizer is a digital filter that provides an approximate inverse of channel frequency response. Equalization is to mitigate the effects of ISI to decrease the probability of error that occurs without suppression of ISI, but this reduction of ISI effects has to be balanced with prevention of noise power enhancement. |
a. Adaptive equalization
|
| Adaptive equalization is an equalizer that automatically adapts to time-varying properties of the communication channel. It is frequently used with coherent modulation such as phase shift keying , mitigating the effects of multipath propagation and Doppler spreading. |
b. Blind equalization:
|
| Equalizer minimizes the error between actual output and desired output by continuous. It is a digital signal processing technique in which the transmitted signal is inferred(equalized) from the received signal, while making used only of the transmitted signals statistics. |
c. Zero Forcing Equalizer
|
| Zero Forcing Equalizer refers to a form of linear equalization algorithm used in communication systems, which inverts the frequency response of the channel. This form of equalizer was first proposed by Robert Lucky. The Zero-Forcing Equalizer applies the inverse of the channel to the received signal, to restore the signal before the channel. It has many useful applications. For example, it is studied heavily for IEEE 802.11n (MIMO) where knowing the channel allows recovery of the two or more streams which will be received on top of each other on each antenna. The name Zero Forcing corresponds to bringing down the inter symbol interference (ISI) to zero in a noise free case. This will be useful when ISI is significant compared to noise. For a channel with frequency response F(f) the zero forcing equalizer C(f) is constructed by C(f) = 1 / F(f). Thus the combination of channel and equalizer gives a flat frequency response and linear phase F(f)C(f)=1. If the channel response for a particular channel is H(s) then the input signal is multiplied by the reciprocal of this. This is intended to remove the effect of channel from the received signal, in particular the Intersymbol Interference (ISI). |
d. MMSE Equalizer
|
| A minimum mean square error (MMSE) estimator describes the approach which minimizes the mean square error (MSE), which is a common measure of estimator quality. The main feature of MMSE equalizer, is that it does not usually eliminate ISI completely but, minimizes the total power of the noise and ISI components in the output. Let x be an unknown random variable, and let y be a known random variable. An estimator x^ (y) is any given function of the measurement y, and its mean square error is given by |
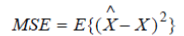 |
| Where the expectation is taken over x and y. The MMSE estimator is then defined as the estimator achieving minimal MSE. In many cases, it is not possible to determine a closed form for the MMSE estimator. In these cases, one possibility is to seek the technique minimizing the MSE within a particular class, such as the class of linear estimators. The linear MMSE estimator is the estimator achieving minimum MSE among all estimators of the form AY + b. If the measurement Y is a random vector, A is a matrix and b is a vector. |
| Assuming the case where two symbols are interfered with each other. In the first time slot, the received signal on the first receive antenna is |
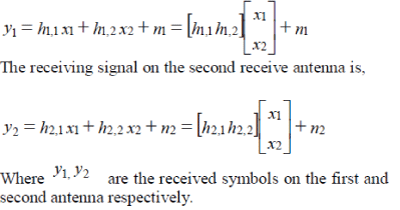 |
| Where y1, y2 are the received symbols on the first and second antenna respectively. h1,1 is the channel from 1st transmit antenna to 1st receive antenna. h1,2 is the channel from 2nd transmit antenna to 1st receive antenna. h2,1 is the channel from 1sy transmit antenna to 2nd receive antenna h2,2 is the channel from 2nd transmit antenna to 2nd receive antenna. |
 |
| Where , W- equalization matrix and H- channel matrix. This matrix is known as the pseudo inverse for a general m x n matrix where, |
 |
e. ML EQUALIZER
|
| Maximum-Likelihood (ML) equalizer is a non linear equalizer in which a search is performed over all possible symbols and the most likely one is chosen. It calculates the Euclidean distance between the received signal vector and the product of all possible transmitted signal vectors with the given channel H, and finds the one with the minimum distance. No noise enhancement takes place and numerical issues are virtually not present, as no matrix inversions or divisions are necessary. The ML equalizer tries to search the most likelihood one which minimizes, |
 |
f. Constant Modulus algorithm(CMA) Equalizer
|
| CMA is a blind channel estimator. In many modulation schemes, such as frequency modulation(FM) and phase modulation(PM), the signal to be transmitted possesses a constant envelope. The received signal, however, has lost this property due to multipath and interference effect. The CMA restores the constant envelope property of the signal and increases the SNR. This algorithm thus employs just the a priori knowledge about the envelope of the transmitted signal and has the nice characteristics that no reference signal is required. |
| Blind equalization finds important application in data communication systems. In data communication systems, digital signals are generated and transmitted by the sender through an analog channel to the receiver. Linear channel distortions as a result of limited channel bandwidth, multipath fading is often the most serious distortion in digital communication system. |
| Blind equalization improves system bandwidth efficient by avoiding the used of training sequence. The linear channel distortion, known as the Inter-symbol interference(ISI), can severely corrupt the transmitted signal and make it difficult for the receiver to directly recover the transmitted data. Channel equalization and identification has proven to be an effective means to compensate the linear distortion by removing much of the ISI. |
| To improved the overall throughput of a transmission system, the used of a training period is avoided by performing blind equalization on the receiver side. Among all algorithm, for blind equalization, the constant modulus algorithm(CMA) play a vital role. One of the important features of CMA is that it can equalise constant modulus as well as non-constant modulus(like QAM) signals.CMA has two values, positive and negative. It takes the values of +ve errors and plot the graph. |
| This algorithm is designed to penalize the deviations of the blind equalizer output from a constant modulus. The cost (output) function of CMA algorithm is given by |
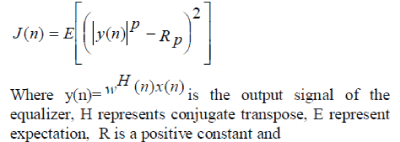 |
 |
IV.QPSK MODULATION
|
| Quadrature Phase Shift Keying (QPSK) is the digital modulation technique. Quadrature Phase Shift Keying (QPSK) is a form of Phase Shift Keying in which two bits are modulated at once, selecting one of four possible carrier phase shifts (0, Π/2, Π, and 3Π/2). It is widely used in wireless communication that uses four points on the constellation diagram, equispaced around a circle. With four phases, QPSK can encode two bits per symbol, shown in the Fig. with gray coding to minimize the BER. By quadrature means the signal shifts between phase states which are separated by 90 degrees. The signal shifts in increments of 90 degrees from 45 to 135, –45, or –135 degrees. These points are chosen as they can be easily implemented using an I/Q modulator. Only two I values and two Q values are needed and this gives two bits per symbol. There are four states because 22 = 4. As it has four states so it is a more bandwidth-efficient type of modulation than BPSK, possibly twice as efficient. |
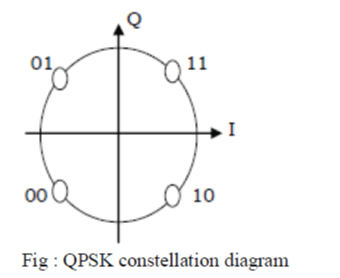 |
V.PROPOSED ALGORITHM
|
 |
B. Steps
|
| 1. Start |
| 2. Generation of random data→104 bits. |
| 3. Creating offset. |
| 4. Counting errors by ML Equalizers. |
| 5. Counting errors by ZF Equalizers. |
| 6. Counting errors by MMSE Equalizers. |
| 7. Estimation of Equalizers via Constant Modulus algorithm(CMA). |
| 8. Calculating the errors |
| 9. Equalizing the errors. |
| 10. Repeat multiples values of BER vs SNR. |
| 11. Plot the graph. |
VI. SIMULATION RESULTS
|
| We consider a MIMO-OFDM system with QPSK modulation. The following parameters are used for simulation. |
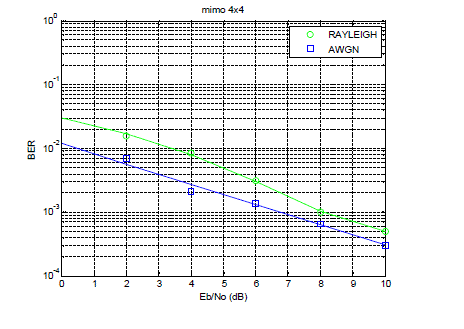
| In Fig. 1, we compared the Rayleigh fading channel with the theoretical AWGN for 4*4 mimo configuration |
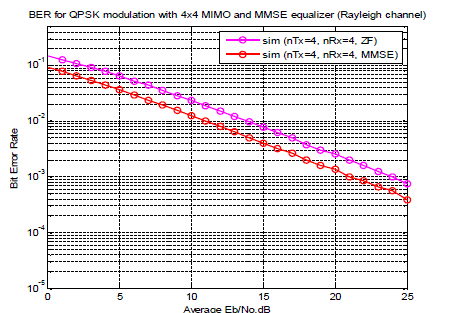
| Figure2 shows the comparision between ZF and MMSE equalizers. From the result its observed that with MMSE technique bit error rate is decreased by certain amount as that with ZF technique for 4*4 antenna configuration in Rayleigh Channel. |
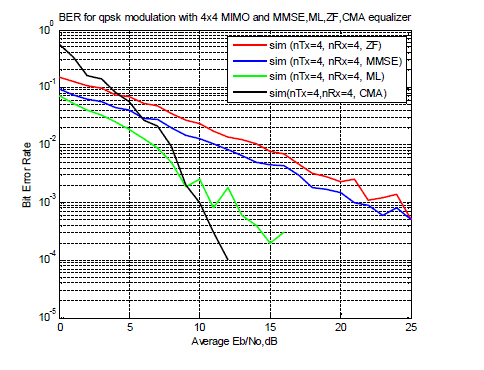
| The BER values have been computed as a function of SNR for QPSK modulation and different combinations of MIMO systems using ZF, MMSE, ML and CMA equalizers. The simulation studies have been carried out using MATLAB software. Performance of CMA equalizers over ZF, MMSE and ML has been described by the figure 3.From this graphical analysis, it is evident that BER tends to decrease dramatically for Constant Modulus Algorithm(CMA) equalizer compared to ZF, MMSE and ML equalizers. |
VII. CONCLUSION
|
| In this paper,an idea about the optimal BER in MIMO wireless communication system at higher modulation levels and antenna configuration is presented. The performance is analysed for 4*4 MIMO configurations in the forms of QPSK modulation under Rayleigh fading channel. A novel equalizer which is term as Constant Modulus Algorithm(CMA) outperforms ZF, MMSE and ML in terms of data rate and BER performance is the outcome of the present paper. |
Tables at a glance
|
 |
| Table 1 |
|
| |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
| |
References
|
- S.Nagarani, C.V.Seshiah, 2011. “An Efficient Space-Time Coding for WirelessCommunication”.European Journal ofScientific Research Vol.52 No.2 pp.195-203.
- S. Yang, J. C. Belfiore, G. Rekaya, and B. Othman, “Perfect space time block codes for parallel MIMO channels,” IEEETrans. Inf. Theory, vol. 13, pp. 1949–1953, Jul. 2006.
- G. L. Stiiber, J.R. Berry, S.W.McLaughlin, Y.G.Li,M.A. Ingram and T.G.Pratt “Broadband MIMO-OFDM WirelessCommunications,” Proc. IEEE, vol. 92, no. 2, pp. 271-294, February, 2004.
- G. J. Foschini and M. J. Gans, “On limits of wireless communications in a fading environment when using multiple antennas,” Wireless Personal Communication, vol. 6, pp. 311-335, Mar. 1998.
- V. Jagan Naveen, K. Murali Krishna, and K.RajaRajeswari, “Performance analysis of equalization techniques forMIMO systems in wireless communication,” International Journal of Smart Home, vol.4, no.4, October, 2010.
- Jiang Yue, Kyeong Jin Kim, Kerry D. Gibson, Ronald A. Iltis,”Channel Estimation and Data Detection for MIMO-OFDM Systems,”GLOBECOM 2003.
|