Keywords
|
| Optimal Reactive power flow, optimal power flow, swarm based algorithm, Firefly algorithm. |
INTRODUCTION
|
| Day to day life growth the Requirement of Electricity when the continuous increase of the population so till daysthe generations are not satisfy the demand.So, Demand of power generations are produce the transmission capacity increase, insufficient reactive power sources,voltageinstability, these are the particular problem for voltage collapse. This is the important problem of power systems. When the power system consist manyproblems these problems are handle to solve optimal power flow method. |
| This power flow studies are of great importance in planning and designing the future expansion of power systems as well as in determining the best operation of existing systems. The principal information obtained from a power-flow study is the magnitude and phase angle of the voltage at each bus and the real and reactive power flowing in each line. When the deriveof optimal power flow (OPF) is schedule the power systems control also minimize the electrical losses in transmission systems.This optimal power flow problem solves the non-linear equality and inequality constraints [1]. |
| This optimal power flow problems are handle by reallocate of reactive power generation.when these solved by change the generator bus voltage,VAR output, transformer tap setting, are the shunt compensating devices. This is the control parameter in Optimal reactive power dispatch (ORPD). In extra the real power loss minimized and voltage profile maximized help of reallocate of reactive power generation [2,3].Some metaheuristic algorithms methods are handle optimal power flow problems and able to achieve a target of global optimal solutions. Manymetaheuristic algorithmsare not achieve a target of global optimal solution.This paper reviewed about new algorithm of Firefly and this algorithm how to handle to solve optimal power flow problems and how to target better global optimal solutions are briefly discussed in this paper[4 - 15]. |
OPTIMAL POWER FLOW
|
| The optimal power flow of OPF has contain long time to its improvement. These method first explained by Carpentier in 1962 and take a lot of time to become a achieve victory of algorithm that could be involvedin everyday use. Current aim in the OPF middle around contain to achieve for the optimal solution that contain data of the protection of the system. |
| If we think about the single “generation equals load plus losses” constraint: |
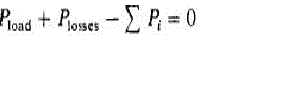 |
| In the OPF, there are many more adjustable or “control” variables that be specified. A partial list of such variables would include: 1) Generator voltage. 2) LTC transformer tap position. 3) Phase shift transformer tap position. 4) Switched capacitor settings. 5) Reactive injection for a static VAR compensator. 6) Load shedding. 7) DC line flow. |
| The OPF has many applications including: |
| 1) The determination of the optimum generation method, as well as include all control parameter, to achieve the minimum cost of generation. |
| 2) The OPF can be used periodically to find the optimum setting for generation voltages, transformer taps and switched capacitors or static VAR compensators (sometimes called “voltage-VAR” optimization). |
| 3) The current steadystate of the power system or a short duration load forecast, the OPF can be fixed to provide a “preventative dispatch”. |
| 4) The emergency state, contain a some equipment of the system is overloaded or a voltage limitation, the OPF can set a “corrective dispatch”. |
| 5) The OPF is continuously used in calculations to determine the high stress that a planned transmission system can withstand. . |
OPTIMAL REACTIVE POWER DISPATCH
|
| The Main aim of ORPD is to minimize the Real powerloss (PLOSS) in the transmission system. There are two basicapproaches to loss reduction, namely the generator bus techniqueand the equation of losses on particular lines.Meanwhile it is find to Reducelosses in a particular area. the another method which is more generic, is usedin this work |
EXISTING SYSTEMS
|
| Existing system methods lists are given A) Biogeography Based Optimization (BBO) B) Hybrid Particle Swarm Optimization (HPSO) C) Differential Evolution (DE)D) Multi objective Evolutionary Algorithm.(EA) E) Real Coded Mixed Integer Genetic Algorithm (RCMIGA). |
| A. Biogeography-Based Optimization |
| Biogeography method is reviewed about the nature’s way of separating Biological Organism. This technique contain Migration and Mutation. And it is solved by two method first one for Habitat Suitability Index(HSI) these technique contain Diversity of vegetation, Rainfall, temperature, diversity of nature organism of land area. This HSI contain of Dependent variable. Remainingone issuitability Index Variable (SIV) it refered independent variables. |
| This method eligible to handle multi constrained optimal power flow problem in power system. Multi constrained means to minimize the Real power loss and also simultaneously minimize the voltage deviation. When real power loss and voltage deviation reduce the help of adjust control variable are Generator Voltage magnitude, VAR sources, and tap setting. |
| B. Hybrid Particle Swarm Optimization |
| This paper technique contain food finding behaviour of birds and the HPSO method handle to minimize the real power loss. When the loss is minimized using two techniques, one is tangent vector method the vulnerability area of the power system is find. Remaining one is find the area, the HPSO method takes space to reduce the amount of shunt reactive power compensation in every bus. When real power loss is reduce the help of adjust control variable are Generator Voltage magnitude, VAR sources, and tap setting. |
| C. Differential Evolution: |
| This differential Evolution optimization method eligible to solve optimal power flow problems and to calculate non convex optimal power flow problems also decrease the real power loss. This optimization method achieved by adjustment of some control parameters that are generator terminal voltage, tap position these are the variable to minimize the real power loss. |
| D. Multi objective Evolutionary Algorithm |
| This technique present Optimal reactive power dispatch problem is included. This algorithm used to minimize real power loss and voltage deviations are to be optimized simultaneously. |
| This Multi objective Evolutionary Algorithm eligible to handle a new strength Pareto Evolutionary based method used. When the loss reduction achieved by adjust the some control variabless that are Transformer taps, generator voltage, switchable VAR sources. |
| E. Real Coded Mixed Integer Genetic Algorithm |
| Real coded mixed integer Genetic algorithm one of the method to calculate optimal power flow problems. It is able to solve the nonlinear optimal power flow (OPF) problems. It is eligible tohandle with the continuous and discontinuous parameters. The continuous parameter consist of generator bus voltage magnitude and values of static VAR Compensators.VAR injection, Discrete parameter contain ofphase shifter, transformer tap settings and angle positions, this method able to achieve a better target of global optimal solution. |
PROPOSED SYSTEMS
|
| 5.1. Firefly Algorithm |
| The algorithm invented byDr.Xin she yang at Cambridge University in the year of 2008.these algorithm inspired by mating or flashing behaviour of fireflies. These paper Reviewed to solve non-linear design problems.This method used to optimize real power loss and ability to improve the voltage profile and these are able to succeed by with help of to adjustment of some the control parameters that are transformer tap settings and VAR outputs from shunt compensating devices are the control variables. And this paper explained using firefly technique find to achieve global optimal solutions are described below. To achieve global optimal solutions is find with the help of two test functions first one is singularity (or) stochastic remaining one is deterministic. |
| Stochastic method produce separate or unequal solution even the same starting point. Deterministic method produce the same set of solution that mean produce equal solution of even with the same initial starting point. These Deterministic algorithm aretoefficient to find local optima. It is complexity to find the betterglobal optimal solution. So, stochastic method preferable to find global optimal solution. Many stochastic algorithms consist as meta-heuristic, and better examples are genetic algorithms (GA) and particle swarm optimization (PSO). Many modern meta-heuristic algorithms are developed by based on the swarm intelligence in nature.Stochastic method can take many forms such as simple randomization by randomly sampling the search space. |
| 5.2. Fireflies Working Criteria: |
| The fireflies consist are the following rules are described given below. |
| 1) Fireflies are unisex so consist of one firefly is interact to remaining fireflies regardless of their sex. |
| 2) Attractiveness is directly proportional to their intensity thus for contain randomly two flashing fireflies the low brighter one will move towards the maximum brighter one. |
| 3) The brightness of a firefly is find by the landscape of the objective function to be optimized |
| 5.3 Distance |
| The distance consist of randomly two fireflies betweeni and j at xi and xj respectively, the Cartesian distance formula is find by equation where xi, when k consist the kth component of the spatial coordinate xi of the ith firefly and d contain the number of dimensions. |
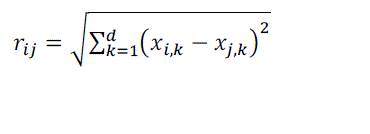 |
| 5.4 Movement |
| The movement between a two firefly is determinedi is attracted to another more high brighter firefly j is calculated by |
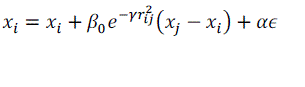 |
| 5.5Algorithm |
| Step 1: Start the coding |
| Step 2: Enter the value of load system input data |
| Step 3: To calculate initial population of firefliesxi (i= 1, 2, ..., n) |
| Step 4: To find brightnessIi at xi is determined by f(xi) |
| Step 5: Set the iteration count toiter=1 |
| Step 6: To find ith firefly for i= 1 to distributen to all n fireflies |
| Step 7: To calculate jth firefly for j = 1 to distributen toall n fireflies |
| Step 8: To findif (Ij> Ii), Move firefly itowards j in d-dimension; to condition satisfy the program end if |
| Step 9: Above condition not satisfy To determine attractiveness, when Attractivenessvariy depend on distance r. |
| Step10: To calculate new solutions and update light Intensity |
| Step11: end for j |
| Step12: end for i |
| Step13: Oreder the firefly and determine the current best value |
| Step14: To Calculate Iter=Iter+1 |
| Step15: Checkif Iter>Iter max; the given condition not satisfy means go to step 4. |
| Step16: Preview the results |
| Step17: Stop the program. |
PERFORMANCE EVOLUTION
|
| The program performance of the proposed Firefly algorithm based reactive power optimization method is tested on the any sizeof IEEE bus system. The algorithm is implemented using MATLAB program and a Core 2 Duo, 2.8 MHz, 2GB RAM based PC is for the simulation purpose. |
| The control variables are Generator bus voltage magnitudes, transformer tap settings and VAR outputs from shunt compensating devices are the control parameters in optimal power flow problems. These control parameter values are adjusted for loss reduction. |
| The test system taken has six generating units connected to buses 1,2,5,8,11 and 13. There are 4 regulating transformers connected between bus numbers 6-9, 6-10, 4-12 and 27-28. Two shunt compensators are connected in bus numbers 10 and 24. The system is interconnected by 41 transmission lines. |
CONCLUSION
|
| In this paper reviewed Novel firefly programing method for function optimization explain a literature survey about on Firefly algorithm these method is clearly explained able to solve optimal power flow non-linear problems. And these algorithm clearly explained about at distance, attractiveness, movement ,light intensity, is explained using these parameters are able to solve multi constraint optimal power flow problems are using Firefly algorithm simultaneously to optimize real power loss and voltage deviation are both minimized also it achieves better global optimal solution. |
ACKNOWLEDGMENT
|
| This work was done at S.K.P Engineering College. The authors would express to thank S.K.P Engineering College for the technical encourage. |
Tables at a glance
|
 |
| Table 1 |
|
| |
Figures at a glance
|
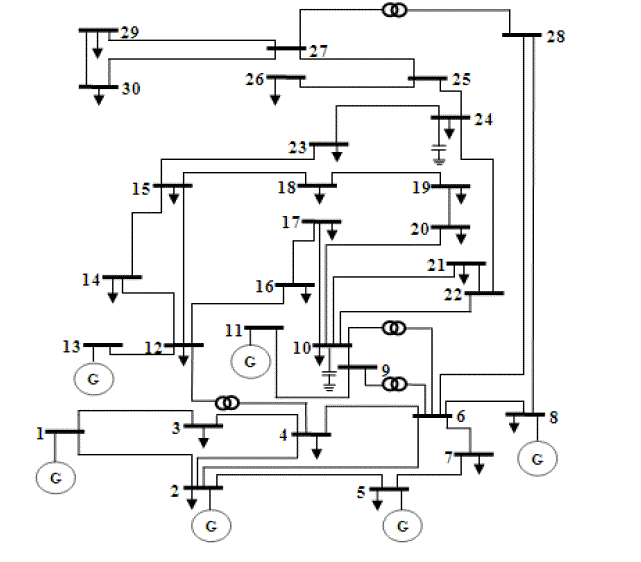 |
| Figure 1 |
|
| |
References
|
- Mamandur KRC, Chenoweth RD. Optimal control of reactive power flow for improvements in voltage profiles and for real power loss minimization. IEEE Trans Power ApparatSyst1981;PAS-100(7):3185–93.
- Mansour MO, Abdel-Rahman TM. Non-linear VAR optimization. Usingdecomposition and coordination. IEEE Trans Power ApparatSyst1984;PAS-103(2):246–55.
- Lai LL, Ma JT. Application of evolutionary programming to Reactive power planning-comparison with nonlinear programming approach.IEEE Trans Power Syst1997;12(1):198–206.
- Yoshida H, Kawata K, Fukuyama Y, Takayama S, Nakanishi Y. A particle swarm optimization for reactive power and voltage control considering voltage security assessment. IEEE Trans Power Syst2000;15(4):1232–9.
- Vlachogiannis JG, Lee KY. A comparative study on particle swarm optimization for optimal steady-state performance of power systems. IEEE Trans Power Syst 2006;21(4):1718–28.
- Swain AK, Morris AK. A novel hybrid evolutionary programming method for function optimization. In: Proc 2000 congress on evolutionary computation, vol. 1, July 2000. p. 699–705.
- Abido MA, Bakhashwain JM. Optimal VAR dispatch using a multiobjective evolutionary algorithm. Int J Elect Power Energy Syst 2005;27(1):13–20.
- Gaing Z, Huang HS. Real-coded mixed integer genetic algorithm forconstrained optimal power flow. In: IEEE TENCON region 10 conference, 2004, vol. 3, November 2004. p. 323–6.
- Lee JC, Lin WM, Liao GC, Tsao TP. Quantum genetic algorithm for dynamic economic dispatch with valve-point effects and including wind power system. Int J Elect Power Energy Syst2011;33(2):189–97.
- Simon D. Biogeography-based optimization.IEEE Trans EvolutComput 2008;12(6):702–13.
- P.K. Roy, S.P. Ghoshal, S.S. Thakur, “Optimal VAR Control for Improvements in Voltage Profiles and for Real Power Loss Minimization using Biogeography Based Optimization”, Electrical Power and Energy Systems, Vol. 43, No.1, pp. 830–838, December 2012.
- X. S. Yang, “Firefly algorithm, stochastic test functions and design optimisation,” International Journal of Bio-Inspired Computation, vol. 2, no. 2, pp. 78–84, 2010.
- X. S. Yang, Nature-Inspired Meta-Heuristic Algorithms, LuniverPress, Beckington, UK, 2008.
- Wood AJ, Woollenberg BF. Power Generation Operation and Control. 2nd ed. New York; Wiley; 1996.
- MohdHerwanSulaiman, HamdanDaniyalMohdWazir Mustafa “Modified Firefly Algorithm in Solving Economic Dispatch Problems with Practical Constraints” 2012 IEEE International Conference on Power and Energy (PECon), 2-5 December 2012, Kota Kinabalu Sabah, Malaysia.
|