A Novel IEEE 754 Standard Floating Point
Unit Comprising Fused Add-Subtract Unit

Rosemin C.J.; Anuja George; Arundev V

A Novel IEEE 754 Standard Floating Point Unit Comprising Fused Add-Subtract Unit

Rosemin C.J.¹, Anuja George¹, Arundev V²

Department of Electronics and Communication, St. Joseph’s College of Engineering and Technology, Palai, India
Flight Computer Division, FCG/AVN/VSSC, Kerala, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In this paper, a high speed and reduced area floating point unit(FPU) is implemented incorporating fused addsubtract unit. The FPU is designed to handle numbers both in single precision and double precision formats. When compared to discrete add-subtract unit, fused add-subtract unit has achieved 33% reduction in area and 52% reduction in delay in case of single precision format. In double precision format compared to discrete add-subtract unit, fused add-subtract unit has achieved a reduction in area and delay by 41% and 40% respectively. The FPU was designed using VHDL language and implemented on a Xilinx Virtex-II FPGA.

Keywords

Discrete FPU, Fused FPU, VHDL

INTRODUCTION

The computer arithmetic units in a modern microprocessor execute advanced applications such as 3D graphics, multimedia, signal processing and various scientific computations that require complex mathematics. Real numbers are mainly divided into fixed point and floating point numbers. Programming languages supports numbers with fractions which is called as floating point numbers. Compared to fixed point numbers, floating point numbers can represent wide range of values. Range of values varies from very tiny numbers to very large numbers. To retain the resolution and accuracy many of the researchers go for floating point numbers.

Precision plays an important role in the floating point numbers. We are dealing with both single precision and double precision floating point numbers in this paper. A floating point number is usually represented as, significant * baseexponent . Base is implicit and need not be stored because it is same for all numbers. To make arithmetic operations simple on floating point numbers, it is typically required that they be normalized. A normalized number is one in which the most significant digit of the significand is nonzero [4].

The floating point representation is defined in IEEE standard 754, adopted in 1985. Floating point numbers have three fields such as sign, exponent and mantissa [1]. The bits that corresponds to these fields depends on the precision. In single precision there will be 32 bits and in double precision 64 bits. The arrangement of both formats is given in fig.1.

In the formats shown in the fig.1, S represents the sign of the number. The value 1 for S indicates that number is negative and 0 indicates number is positive. E denotes the exponent and M is the mantissa. Mantissa is otherwise called as significand. IEEE 754 uses biased representation for the exponent. That means Val(E)=E-Bias(Bias is a constant). This is chosen to make the biased exponent’s range nonnegative [1].

IEEE 754 standard defines three special numbers- signed zeros, signed infinities and NaNs. These three are considered in the design of this paper.Also our design detects all five IEEE floating point exceptions – invalid operation, underflow, overflow, inexact and divide by zero [1]. Floating point addition and subtraction are more complex arithmetic operations compared to multiplication and division. If the addition and subtraction is combined to a single unit, it will lead to better performance of the floating point unit. Many designs were proposed for the designs of fused floating point addsubtract unit.

The paper is arranged as follows: Section II deals with floating point addition algorithm proposed in this paper and principles used in the fused floating point add-subtract unit. Other arithmetic operations such as multiplication, division, squaring and inversion are described in Section III. In Section IV, the synthesized results of the experiments carried out are given. And section V concludes the paper.

PROPOSED FUSED FLOATING POINT ADD-SUBTRACT UNIT

A. Floating point addition algorithm

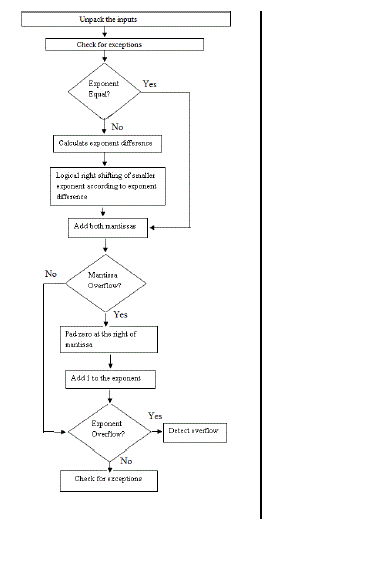
Floating point addition and subtraction are the main arithmetic operations dealt with this paper. In both operations it is necessary to ensure that both operands have same exponent value. The flow chart for the floating point adder used in this paper is given in the figure 2. Steps in the proposed algorithm for floating point addition are given below.

Step 1: Unpack the inputs into three fields such as sign, exponent and mantissa.

Step 2: In the first stage exceptions at the input side is found out. If any of the input is NaN(Not a number), then output is taken as null. If both the inputs are zero or infinity, then output is taken as zero or infinity respectively.

Step 3: The exponent difference between two inputs is found out. If there is no exponent difference, then the significands of both inputs are added together. Otherwise the mantissa of smaller exponent is padded with zeros at the right according to exponent difference. And the smaller exponent made equal to larger exponent.

Step 4: Significands of both inputs are added together after logical right shifting of significand of smaller exponent.

Step 5: If there is significand overflow, pad zero at the right of the significand and add ‘1’ to the exponent.

Step 6: If there is exponent overflow then detect overflow.

Step 7: Check for exceptions at the output side also.

Floating point subtraction has similar steps as that of addition, and difference comes in the step 4. Here instead of addition of significands, subtraction of significands is done. So if we are doing addition and subtraction in separate blocks, it will lead to excessive area and power consumption. Many works proposed fused floating point add-subtract unit that produces addition and subtraction simultaneously [2],[3],[5]. This paper presents a fused floating point which produces addition or subtraction at a time.

B. Principles used in fused FPU

Sign of two operands decides the operation to be performed is whether addition or subtraction. In the case of floating point addition, if two operands have same sign then addition is to be done otherwise subtraction is to be performed. In floating point subtraction, if two operands have same sign then subtraction should be done otherwise addition should be performed. The above logic indicates that with proper sign logic we can combine both addition and subtraction. Jongwook Sohn proposed a sign decision table which shows the signs of two operands and comparison of the exponents and significands [2].

According to the above sign decision table, the new fused floating point add-subtract unit is proposed in this paper.

OTHER FLOATING POINT ARITHMETIC

Floating point arithmetic is widely used in many scientific and signal processing applications. Implementing arithmetic operations for floating point numbers in hardware is challenging. Multiplication, division, squaring and inversion are the other floating point arithmetic described in this paper.

A. Floating point multiplication

With unsigned multiplication there is no need to take the sign of the number into consideration. However in signed multiplication the same process cannot be applied because the signed number is in 2’s compliment form which yields an incorrect result if multiplied in a similar fashion to unsigned multiplication. That’s where Booth’s algorithm comes in. Booth’s algorithm preserves the sign of the result. There are mainly two rules: append a zero to the right of the LSB of the multiplier number and inspect groups of two adjacent bits of multiplier, starting with the LSB and the appended zero. If the pair is 00 or 11, then shift the partial product one bit to the right. If the pair is 01, then add the multiplicand to the partial product and shift the new partial product one place to the right. If the pair is 10, then subtract from the partial product and shift the new partial product one place to the right.

B. Floating point division

PROPOSED WORK

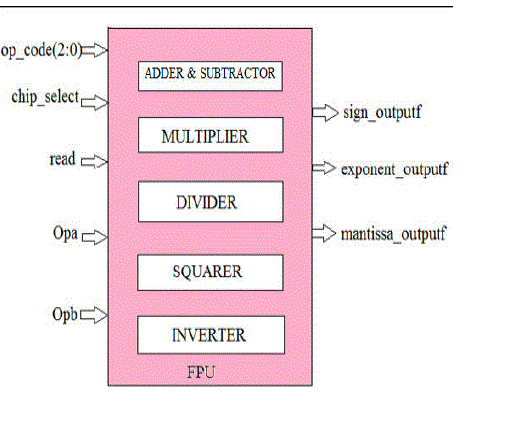
The top module designed is termed as FPU. It consists of five sub modules producing six arithmetic operations. The input op_code is three bits and selects the arithmetic operation to be performed. Opa and opb are the operands that are given to the module.

RESULTS AND DISCUSSIONS

After simulating both discrete and fused floating point add-subtract units, the design is synthesized using Xilinx ISE 13.2. A comparison between discrete floating point add-subtract unit and fused floating point add-subtract unit is done. It is found that both resource utilization and delay is optimized in latter. So fused add-subtract unit is used in the design of our floating point unit resulting in a low power reduced area design.

A. Comparison between discrete & fused floating point add-subtract unit

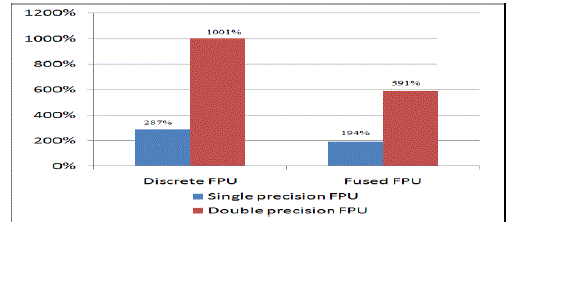
Single precision floating point unit is considered first. Percentage of slices and LUTs used in discrete floating point add-subtract unit is found to be 287% and 272% respectively. In fused floating point add-subtract unit, percentage of slices and LUTs is found to be 194% and 183% respectively. Percentage of LUTs in both is same and that is 81%. Thus it is evident that resource utilization is reduced by 33% in fused floating point add-subtract unit and it leads to a low area design. This is helpful in many critical applications.

Considering the case of double precision floating point unit, percentage of slices and LUTs used in discrete floating point add-subtract unit is found to be 1001% and 950% respectively. In fused floating point add-subtract unit, percentage of slices and LUTs is found to be 591% and 555% respectively. Percentage of LUTs are same and given by 158%. Resource utilization is reduced by 52% by using fused floating point add-subtract unit and represented in the figure 5.

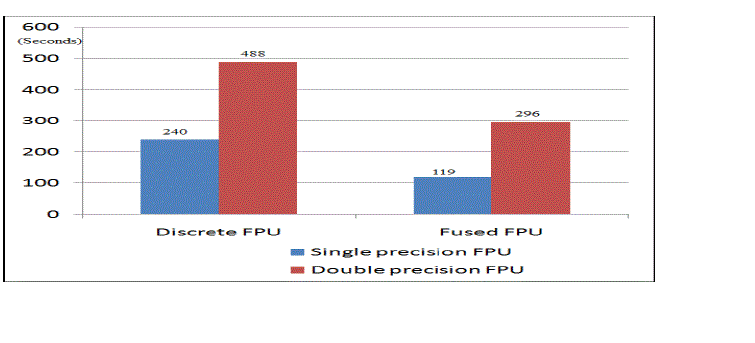
Better performance of fused floating point add-subtract unit is evident from the delay occurred in both. In fused floating point add-subtract unit delay is only 119sec. but in discrete it is 240sec. The difference is plotted in the graph.

B. Evaluation of single precision and double precision floating point units

The design is developed in VHDL language and simulated using ModelSim SE PLUS 6.3f. For the implementations of this circuit we have used Xilinx FPGA (XC2V4000 device of virtex2). The top level source is Hardware Description Language type, with a XST (VHDL/VERILOG) environment.

CONCLUSION

The single precision and double precision floating point units are implemented successfully using fused floating point add-subtract unit. The results obtained using the fused floating point add-subtract unit shows that resource utilization and delay is reduced by 33% and 52% respectively in single precision format and in double precision format area and delay are reduced by 41% and 40%. When compared to discrete floating point add-subtract unit, fused floating point add-subtract unit shows better performance.

Tables at a glance


Table 1	Table 2	Table 3

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4

Figure 5	Figure 6	Figure 7

References

IEEE Standard for Floating-Point Arithmetic, ANSI/IEEE Standard 754-2008, New York: IEEE, Inc., Aug. 29, 2008.

JongwookSohn and Earl E. Swartzlander," Improved Architectures for a Fused Floating-Point Add-Subtract Unit", IEEE transactions on Circuits and Systems, vol.59, pp. 2285-2291, January 2012.

H. H. Saleh and E. E. Swartzlander, Jr., “A floating-point fused add–subtract unit,” in Proc. 51st IEEE Midwest Symp. Circuits Syst., 2008, pp. 519–522.

William Stallings, “Computer Organization and Architecture”, 8th edition Pearson, 2010, pages.345-361, ISBN 978-81-317-3245-8

E. E. Swartzlander, Jr. and H. H. Saleh, “FFT implementation with fused floating-point operations,” IEEE Trans. Comput., vol. 61, no. 2, pp.284–288, Feb. 2012