Keywords
|
| Interval system, order reduction, AGTM matching, model matching, stability. |
INTRODUCTION
|
| In recent decades, much effort has been made in the field of model reduction for linear time invariant system for In recent decades, much effort has been made in the field of model reduction for linear time invariant system for single input single output. Familiar and important methods among them are Pade approximation, Routh approximation, Moment matching technique, and recently H∞ optimization technique[1-16]. Pade approximation method has computational simplicity, but sometimes generate unstable reduced order model for stable higher order model. To resolve the problem of stability, Routh approximation method was introduced, But it is noticed that this type of approximation always tend to approximate the low frequency behaviour of higher order system. Enormous attempts have been made to improve the Routh approximation method and other model reduction techniques. |
| Several types of uncertainties can be present in a control system. This uncertainty in our knowledge of all the parameter values in a system means that whatever mathematical model that use to represent the system will be at best an approximation to the real system. Not only the uncertainty in our knowledge of the system dynamics, but the system will often be subject to perturbations that change those dynamics over time. These perturbations can be due to several factors. Uncertainty can be classified into two categories - aleatoric uncertainties and epistemic uncertainties. First one is the representative of unknowns that differ each time when the same experiment is performing. The second category is due to things we could know in principle but don't in practice. The parametric uncertainties among the structural uncertainty can be represented as variations in coefficient of transfer function. The uncertain systems usually referred as interval systems. Previous publications which relate to the problem of model reduction of systems with uncertainties are very few. Most of the model order reduction techniques for fixed coefficient systems are applicable to interval systems also[19-22]. But sometimes the interval arithmetic operation results in unexpected results and some modification algorithms are used for better result. |
| Controller order reduction is also very important issue in many control applications. Simple linear controller is normally preferred over complex linear controllers for linear time invariant plants. They are easier to understand and the computational requirements are less. As it is well known, uncertainties are way of life in analyzing and designing control systems, it is always desirable to have a design technique which incorporates the uncertainties. For SISO interval plants, there are a few striking results in literature, which address this issue. [23-32]. |
| A few number of investigations have been carried out in literature and various methods are proposed for model reduction for interval systems. Some order reduction techniques ensure only the stability and some other methods ensure the performance matching. Different methods of robust control for interval systems are also proposed in recent literature. A very less effort has been put forward to design the controller for interval system using model order reduction technique. In most of the controller synthesis method, the importance is given to stability only. There is no method available for performance matching along guaranteed stability. Hence the contribution of this work intends to present a method of model reduction and design of controller which will guarantee stability while matching the performance. Details of the developed method are given in the following sections. |
SYSTEM DESCRIPTION AND PROBLEM FORMULATION
|
| The problem of model order reduction for interval system is divided into two phases. In the first phase, nominal transfer function is obtained from given higher order interval transfer function. The order of nominal transfer function is reduced using AGTM matching method in which the optimum selection of expansion points is carried out using the Luus-Jaakola (LJ) optimization procedure. In the second phase, the optimization procedure is done for obtaining the interval parameters. |
| Consider a stable linear time invariant single input single output (SISO) interval system described by the higher order nominal transfer function, |
 (1) (1) |
| where ci ,0≤ i ≤ q and di, (0 ≤ i≤ p-1) are known scalar constants ,q and p are order of numerator and denominator of higher order transfer function. |
 |
| where bi, (0≤ i≤ m) and ai,, (0 ≤ i≤ n-1) are unknown scalar constants, m and n are order of numerator and denominator of low order transfer function. |
| In this paper, a method is proposed to obtain reduced order nominal model in the form of equation (2) such that the reduced order model retains important characteristics of the original system and approximates its response as closely as possible for the same type of inputs. |
| A. DETERMINATION OF COEFFICIENTS FOR THE LOW ORDER MODEL |
| One of the objectives is to obtain the steady state matching. According to the final value theorem for a step input, |
 |
| Equating the two steady state values, g(∞) = r(∞), expression for 0 b is obtained as |
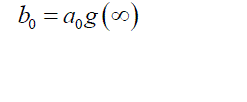 (3) (3) |
| Hence the number of unknown parameters to be found out is reduced by one. |
| Matching the approximate generalized time moments of the higher order model, G(s) with that of the reduced order model, R(s) at the expansion points s =si , i=1,2,3…………(m+n). |
 (4) (4) |
| G(s), for a particular value of frequency, s =si can be written as Vi |
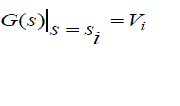 (5) (5) |
| Equating equation (4) and (5) |
 (6) (6) |
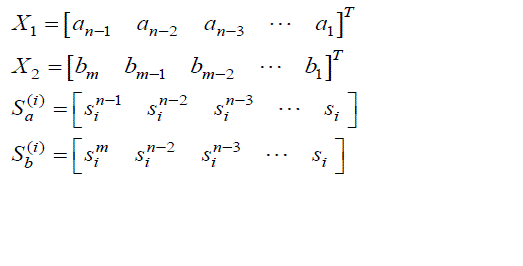 (7) (7) |
| Equation (6) can be written as |
 (8) (8) |
| Equation (8) can be written as |
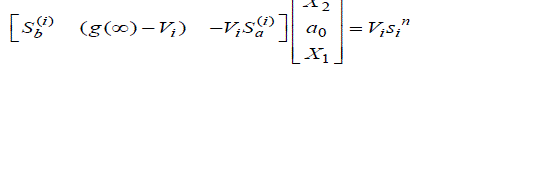 (9) (9) |
| For a particular value of „s? or for a particular frequency, LHS of equation (9) is multiplication of unknown column matrix with a row matrix and RHS is a single value. Hence for another value of „s?, another set is obtained. Thus different rows are obtained for forming matrix A and B. Thus equation ( 9 ) can be written as |
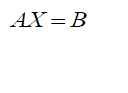 (10) (10) |
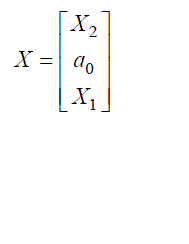 (11) (11) |
| In the equation (10 ) the elements of A and B are known values. Using MATLAB programming, the elements of unknown matrix, X can be obtained. The unknown parameter b0 is obtained from the equation (3). Thus the unknown coefficients of the reduced order nominal model can be obtained. |
| B. SELECTION OF EXPANSION POINTS |
| The expansion points can be a positive or negative real number or a complex point chosen from any of the four quadrants of the s-plane[16]. Care must be exercised that in case of choosing complex points; these should not be in conjugate pairs. In the controller design scenario, the choice of the expansion points, are governed by the stability and performance of the closed loop system. The controller C (s) has to be designed such that the closed loop system responses satisfy the desired specifications, while guaranteeing closed loop stability. No theory is yet available to determine or search the expansion points, such that poles of the resulting closed loop system can be guaranteed to be in the left half of the s-plane. In the present work, this problem of choosing the best expansion points has been cast as a constrained optimization problem which is solved by Luus-Jaakola (LJ) random-search method. The constraint ensures that the chosen expansions points will always yield a stable closed loop system. The number of expansion points, depends upon the number of unknown parameters. |
| C. MODEL ORDER REDUCTION OF INTERVAL TRANSFER FUNCTION |
| For interval transfer function, the first step is to obtain the higher order nominal transfer function of the given higher order interval transfer function. The algorithm explained above is used for getting the reduced order nominal model in the form, |
 |
| The problem of choosing the best ei has been cast as a constrained optimization problem which is solved by Luus-Jaakola (LJ) random-search method. |
 |
METHODOLOGY
|
| The proposed algorithm in the work proceeds as follows. |
| Step 1. The transfer function of the nominal plant is determined from the transfer function of the interval plant. |
| Step 2. Specifying the order of reduced order plant , m and n. |
| Step 3. Giving the initial set of expansion points. ie, the values of „s?. |
| Step 4. From the equation (3 ) and (10 ) the unknown coefficients of numerator and denominator of the nominal reduced order model can be obtained. |
| Step 5. Using Luus – Jaakola optimization technique, best expansion points for the nominal plant can be determined. |
| Step 6. Using this expansion points reduced nominal model can be obtained. |
| Step 7. Using Luus – Jaakola optimization technique, the best range of interval parameters are selected for reduced interval model. |
LOW ORDER CONTROLLER DESIGN
|
| Several approaches are existing for the design of low order controller for linear time invariant single input single output systems with interval parameters. The proposed method is for designing a stabilizing controller for the stable higher order system while preserving the closed loop performance. The indirect approach is adopted for controller design which helps to match the desired closed loop response with the designed closed loop response. |
| A .METHODOLOGY |
| The following steps describe the method for designing the low order controller for linear interval system. |
| Step 1 .In the following figure , G(s) , C(s) and M(s) are the high order interval plant, controller and desired closed loop transfer function respectively. G(s) and M(s) are known. The expected improvement in the system performance is depicted in the desired closed loop transfer function. |
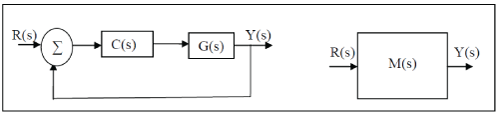 |
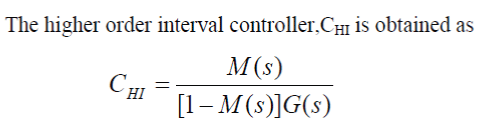 |
| Step 2. The higher order nominal controller is obtained from the higher order interval controller. |
| Step 3. The model reduction method proposed in this paper can also be used for obtaining low order controller. The fundamental difference is, in place of higher order plant, higher order controller is used. In the optimization procedure, closed loop response is considered instead of open loop response which is used in model reduction. |
| The method directly yields a low-order implementable controller of pre-specified structure that ensures stability and captures the essential characteristics of the desired model M(s), based on AGTM matching, LJ optimization procedure and the concept of model matching. |
SIMULATION RESULTS
|
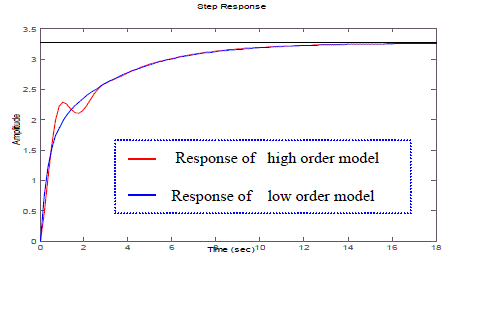
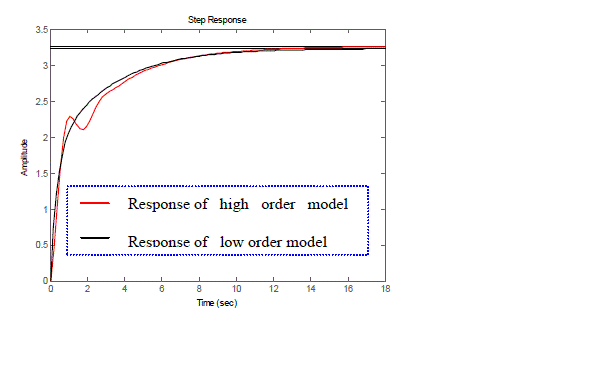
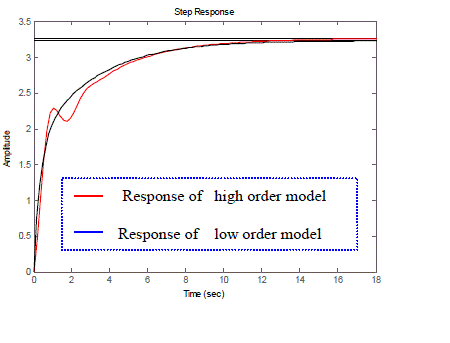
| The developed method of model reduction is applied on different interval transfer function. The interval transfer function in the illustrated example is taken from [21]. In the following example of model order reduction for interval system, proposed method is applied on a seventh order model and the order is reduced to two. The step responses of the reduced order model match very closely with those of higher order model while preserving the stability. The proposed method can be applied for the design of low order interval controller also. |
| For simulation the higher order interval transfer function is given as GI(s) and the reduced order interval transfer function is obtained as RI(s). Nominal transfer function of GI(s) is termed as Gnom and that of RI(s) is termed as Grnom. The order of numerator and denominator of the reduced order transfer function is specified as m and n respectively. Integral square error between higher order model and low order model is obtained as PI . The extreme plants of higher order model and those of the low order model are also compared. The extreme plant of higher order model with lower limits of numerator and lower limits of denominator is termed as G11. The extreme plant of low order model with lower limits of numerator and lower limits of denominator is termed as Gr11. The extreme plant of higher order model with upper limits of numerator and upper limits of denominator is termed as G22 and that of low order model is termed as Gr22. |
NUMERICAL EXAMPLE
|
| The interval transfer function taken from [21] is seventh order .The order is reduced to two, using the developed method of model reduction. |
 |
| From the illustrated example, it is clear that the proposed method can guarantee the performance matching. The step response of higher order model matches very closely with that of low order model. At the same time stability is also preserved. Reduced model of any order can be obtained using the developed method. For using the projected method, there is no restriction to the order of numerator and denominator of the higher order model. |
CONCLUSION
|
| In this paper, a new method of model reduction for linear time invariant SISO interval systems is presented. The method is mathematically simple and easy for computation. Moreover, a reduced order model of a higher order model is obtained with performance matching and guaranteed stability. |
| There are several ways of obtaining a low-order controller for a high-order system. One line of thinking is to first obtain a very accurate higher order model and then apply reduction techniques to this model or to a higher order controller computed from that model. There is an extensive literature on this subject. One of the important theoretical messages of this literature is that, if the ultimate objective is the low-order controller (rather than the low-order model), then it is essential that the closed-loop performance objective be incorporated in the reduction technique. Based on AGTM matching, optimization and model matching, the proposed method of model order reduction can also be used for low order controller design of SISO linear plants subject to interval parametric uncertainty, a longstanding open problem of control theory. Various numerical problems of model order reduction and controller design for interval systems are performed, validated and one example for model order reduction is illustrated for showing the effectiveness of the developed method. Model reduction for any order can be obtained using the presented method. The work can be extended to model reduction and controller design for MIMO interval systems. |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
| |
References
|
- L.Fortuna,G.Nunnari and A.Gallo.Model Order Reduction Techniques with Application in Electrical Engineering.
- Skelton RE.”Cost decomposition of linear systems with application to model reduction”.Int J Contr,32(6):1031-1055, 1980.
- F.Hutton and B.Friedland,”Routh approximation for reducing order of linear time variant systems”, IEEE Transaction on Automat icControl,Vol:AC 20,pp 329-337,June 1975..
- V.Krishnamurthy and V.Sheshadri,”Model reduction using Routh Stability criterion”, IEEE Transaction on Automatic Control,Vol:AC 23,pp 729-730,Aug 1978..
- T.N.Lucas ,”Factor division:a useful algorithm in model reduction”,IEEProc.D.Control Theory&Apllication,130,pp362-364, 1983
- Shamash.Y.Model reduction using the Routh stability criterion and the Pade approximation technique .Int J Contr ,21(3)475-484,1975.
- Shamash,Y.,”Linear system reduction using Pade approximation to allow retention of dominant modes”?International Journal of control,vol. 21,no.2,pp. 257-273,1975.
- Bistritzz.y., “Mixed complete Pade model reduction: A useful formulation for closed loop design”,Electron.Lett.,vot. 16,no.14,pp.563-565,July 1980.
- Pal J., “Stable reduced order Pade approximants using Routh-Hurwitz array”, Electron.Lett.,vot. 15,no.14,pp.225-226,July 1979.
- Pal.J, “Improved Pade approximants using stability equation methods”, Electron.Lett.,vot. 19,no.11,pp.436-427,July 1983.
- Pal.J, “An algorithmic method for the simplification of linear dynamic scalar systems”,International Journal of Control,vol.43,no.1,pp.257-269,1986.
- Davidson.A.M and Lucas.T.N. “Linear system reduction by continued fraction expansion about a general point”,Electron. Lettr.,vol. 10,pp. 271-273,1974.
- Parthasarathy.R and Jayasimha.K.N. “System reduction by Cauer continued fraction expansion about s = a and s =∞ alternatively”, Electron.Lettr.,vol. 18,no. 9,pp. 376-378,1982.
- Pal.J and Ray.L.M, “Improvement of Pade approximation technique in model order reduction”,Proc.IFAC Symposium on theory and application of digital control”,(New Delhi,India),pp. 513-517 , 5-7 January 1982.
- Pal.J,Sarvesh.B, and Ghosh .M.K, “A new method for model order reduction”,Journal of Institute of Electronics and Telecommunication Engineers,vol.41,no.5,pp.305-311,1995.
- Lucas.T.N. “Linear reduction by expansion about s=0 and s=a alternatively”, Electron. Lettr.,vol. 19,pp. 244-246,1983.
- Rivera.D.E and Morari.M,”Control-relevant model reduction problem for SISO using H∞ and μ controller synthesis”, International Journal of Control,vol.48,no.2,pp.505-527,1987.
- V.L.Kharitonov,”Asymptotic stability of an equilibrium position of a family of systems of linear differential equations”,DifferentialUravnen,Vol.14,pp 2086-2088,1978.
- B.Bandhopadhyay,O.Ismail and R.Gorez.”Routh-Pade approximation for interval system”,IEEE transaction on Automatic Control,Vol:39,pp 2454-2456,Dec 1994.
- Yuri Dolgin and Ezra Zaheb,”On Routh -Pade approximation for interval System”, IEEE Transaction on Automatic Control,Vol:48,No:9,,pp 1610-1612,September 2003.
- N.Selvaganesan.”Mixed method of model reduction for uncertain systems”,Serbian Journal of Electrical Engineering,Vol.4.No1,pp.1-12, June2007 .
- Li Li and Ian R.Petersen, “A Gramian based approach to model reduction for uncertain system”,IEEE Transaction on Automatic control, Vol.55,No:2,February 2010.
- Brian.D.O.Anderson Controller reduction ,Concepts and approach,IEEE transaction on Automatic Control,Vol. 34,No:8,August 1989.
- .R.Barmish,”Extreme Point Results for Robust Stabilization of Interval Plants with First Order Compensator”, IEEE transaction on Automatic Control,Vol. 37,No:6,June 1992.
- S.P.Bhattacharya ,“Design of P,PI and PID Controllers for interval Plants”,Proceedings of the American Control Conference,June,1998.
- Didier Henrion and Olivier Bachelier , “Low order robust controller design for interval plants, Intetnational Journal of Control,vol. 74,no.1,page 1-9,2001
- Bhattacharya.S.P,H.Chapellatt and L.H.Keel,RobustControl,The Parametric Approach ,Prentice Hall,1995.
- Benoit Cordrons,P.Bendotti,C.M.Falinower and M.Gevers, “A comparison between model reduction and controller reduction:Application to
- PWR nuclear plant” Proceedings of the 38th Conference on Decision & Control, Phoenix,USA,December1999.
- HamedKebriaei ,AkshanRahimi-Kian , “Robust Control of Interval Systems Using a Pole Placement Design”,IEEE International Conferenceon Control and Automation,China,May 2007. R.Pujara,Arunesh Roy, “On Computing Stabilizing Controllers for SISO Interval Plants”
- Maria Dubravska,LadislavHarsanyi, “Control of uncertain systems” , Journal of Electrical Engineering,Vol.58,N0:4, 228-231, 2007.
- Pal . J, “Control system design using Pade approximation technique”, ICCON 1989,Proc. IEEE International Conference on Control andApplication”,Jerusalem,Israel,pp.WA 5-8,April 1989.
- RadekMatusu,RomanProkop,ZdenkaProkopova, “Simple Tuning of PI Controllers for interval Plant”,Manufacturing and IndustrialEngineering ,11(2),2012.
|