Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

A NOVEL NETWORK REDUCTION TECHNIQUE FOR POWER SYSTEMPLANNING STUDIES WITH CONGESTION PROFILE

M.Thenmozhi1, R.Sathishkumar2
  1. P.G Scholar [Power Management], Dept. of EEE, Anna University Regional Centre-Madurai, Tamilnadu, India
  2. Faculty, Dept. of EEE, Anna University Regional Centre-Madurai,Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The need for studying large scale power systems is increasing due to long distance power transfers and planning of highly interconnected areas. Large systems are difficult to handle if not reduced. This paper focuses on reduction technique yields with a given grouping of buses based on power transfer distribution factors (PTDFs) in order to achieve better calculation performance, easier handling of large amount of data and better observation of the results. This method will be applied for OPF studies, and the OPF results are compared with those from the original networks in terms of the locational marginal prices (LMP), and generation profiles. Modified IEEE 118-bus system and the simulation results are compared has been used to demonstrate the effectiveness of the proposed method.

Keywords
Supply Rich Area (SRA), Demand Rich Area (DRA), Locational Marginal Price(LMP), Power Transfer Distribution Factor (PTDF), Optimal Power Flow (OPF).

INTRODUCTION
Power system planning for the integration on a large-scale power system is computationally challenging. By using small, equivalent networks, the computational requirements can be significantly reduced. But these algorithms have limited applicability in the power system planning, however, due to the high computational cost associated with a large-scale power system. A traditional network reduction method yields a simple model [6]. Equivalent networks reproduce the same voltages and currents of the remaining buses as the original systems do.
However, the power transfer between areas is not preserved because the flows of the eliminated branches cannot be approximated. The creation of large power markets expanding through several control areas, requires new reduction methods focusing on economic criteria and generation participation. Typical methods use either reduction based on locational marginal prices or power transfer distribution factors (PTDFs). The basic idea of the LMP based method is to create clusters, e.g. aggregated areas, based on locational marginal prices. In order to avoid creating clusters where congested lines exist, only nodes with similar nodal prices are aggregated. In order to calculate the initial nodal prices an optimal power flow (OPF) calculation for clustering is required, which means that the detailed initial system has to be known. For large scale systems and for systems that extend within more than one control area, this calculation might not be possible due to lack of information.
Power transfer distribution factors (PTDFs) that indicate how, in terms of percentage power flow, a bilateral transfer of a specific amount of power influences the rest of the transmission network. Thus, a reduction based on PTDFs is, depending on the actual configuration of the system, as in case of LMP method application. A reduction method based power transfer distribution factor (PTDF) is proposed to preserve the same flow pattern as that in the original network.
A new method to reduce network was recently proposed to construct the flow sensitivity matrix to the reduced injection. The reduced injections and the reduced flows are defined as the aggregated injections and the aggregated flows at a predefined group of buses. From the procedure, the method yields a simple but precise injection profile independent model. However, It is not clear how a group of buses should be defined. As a result, the injection and the flow profiles might be significantly different if the original network is used for an optimal power flow (OPF) study.In OPF studies, congestion often increases the system cost significantly because it may keep cheap generation from being dispatched. Congestion plays a critical role in OPF and planning studies. Because congestion arises where flow over a line equals the limit of the line, it is important to assign the flow limits for the studies. Therefore, it is also important to assign adequate flow limits for the aggregated lines (corridor). Even though the reduction algorithm yields a simple but precise model, its applicability can be limited without the proper assignment of the flow limit.

IMPORTANCE OF NETWORK REDUCTION
Network reduction or equivalence has become important for several reasons and in several different applications. Real time observation of the network demands very high computational effort for repeated calculations in order to provide the system with security of supply. Additionally, the integration of renewable energy sources into the system requires power transmissions over longer distances, and it is necessary to evaluate the limitations of the transmission network. Power flow and optimal power studies for large-scale networks are needed both for operational or planning purposes. The reduction methods are divided in static and dynamic according to the representation of the model:
A. Static Reduction
The reduced model represents a snapshot of the system and is suitable of static analysis only. These kinds of models are appropriate for power flow calculations, for operational and planning analysis.
B. Dynamic Reduction
The reduced model is used for (a) large scale power system offline transient stability analysis with large disturbance, (b) large scale power system off -line dynamic stability analysis with small disturbance, (c) large scale power system on-line security assessment.
Here, a new method is proposed to find a proper grouping of buses for the reduction and to assign the flow limits so that the congestion profile is preserved. The algorithms for the bus grouping and for the assigning flow limits are key features for preserving the congestion profiles. The method will be applied for Optimal Power Flow (OPF) studies, and the OPF results are compared with those from the original networks in terms of the congestion profiles, the locational marginal prices (LMP), and generation profiles.

POWER SYSTEM NETWORK REDUCTION
A. Network Reduction Procedure
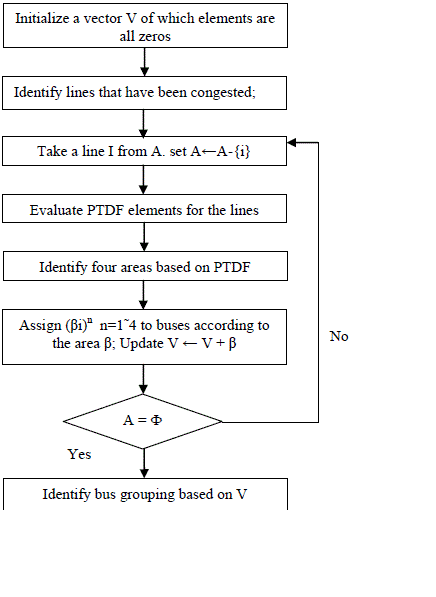
A brief description of the network reduction method is as follows:
1) First, define areas so that all the buses inside an area have similar properties.
2) Ignore all the lines connecting two buses that belong to the same area.
3) Lines connecting two buses that belong to different areas are aggregated.
4) PTDF of the reduced network is computed.
5) Reactance values for the reduced network are computed from the PTDF obtained in 4 and the node-branch incidence matrix for the reduced network.
A simple but precise reduced model is obtained from the process if the areas are provided. [3] showed that power flow studies with the reduced model yield similar flow patterns. However, it is not clear how to determine the areas. For defining the areas, the buses inside an area should have similar properties. For optimal planning studies, significant importance is imposed on the economic impacts. Therefore, properties related to the economic impact need to be considered. Because LMP reflects the impact, the areas are defined based on the price. Therefore, area is a set of busesof which LMP falls into a similar value. When a line is congested, the power injected from one end of the line equals the one ejected from the other end if losses are ignored. At the ejection side, the power is deficient; i.e., the sum of loads is greater than that of generations. The area is termed demand- rich area (DRA). The congestion results in higher LMP than the system marginal cost. The injection side is termed supply-rich area (SRA) because the sum of loads is less than that of generation. The congestion results in lower LMP than the system marginal cost.
B. Separation of Network due to Congestion
When a line is congested, the power injected from one end of the line equals the one ejected from the other end if losses are ignored. At the ejection side, the power is deficient; i.e., the sum of loads is greater than that of generations. The area is termed demand-rich area (DRA). The congestion results in higher LMP than the system marginal cost. The injection side is termed supply-rich area (SRA) because the sum of loads is less than that of generation. The congestion results in lower LMP than the system marginal cost.
C. Bus Grouping Algorithm
For each bus set β. β is the Scalar to identify the membership of bus according to a congested line. For the buses that belong to the same sets, the sum of the number (Σβn) should be equal. After such assignment, select all the buses to which the sum of the numbers assigned is equal. Note that the value for is selected so that the sum of a bus unequivocally yields the membership to which the bus belongs. With the choice, four groups are classified for each congested line: SRA bulk, SRA near boundary, DRA bulk, and DRA near boundary. The values for are 1, 2, 3, and 4 for SRA bulk, SRA near boundary, DRA bulk, and DRA near boundary, respectively.
With given values of PTDFs of each line four areas for each congested line are assigned. It is possible to define sets from a network provided the congestion profile is given. Suppose there existN sets. For each set n, the buses that belong to the set are given βnwhere β>1.
For the buses that belong to the same sets, the sum of the number (Σβi) should be equal. After such assignment, select all the buses to which the sum of the numbers assigned is equal. Note that the value for is selected so that the sum of a bus unequivocally yields the membership to which the bus belongs. In this process, the congested lines belong to the intergroup lines [3]. Suppose a congested line connects two groups, and there exist other lines connecting the same groups. The method in [3] yields a way to aggregate all the lines connecting the groups. However, as mentioned in the Introduction, the flow limits are difficult to assign. Instead, the lines connecting two groups except the congested one are aggregated into a single line parallel to the congested line.
D. Limitation of Proposed Work
The proposed method yields a way to group the buses to preserve the congestion profiles that the original network has. A purpose of the network reduction is for planning studies. Therefore, it is possible for unanticipated sets of congestion to occur. If the congested lines yield a completely different congestion profile, then the result from this algorithm may not reflect the proper congestion profiles. Therefore, it is important to include possibly congested lines as well as existing congested lines.

SIMULATION AND DISCUSSIONS
In this chapter results have been presented the implementation of the theories discussed in the above chapters. The new network reduction algorithm has been developed by using MATPOWER. The algorithm has been tested on IEEE 118- bus system.
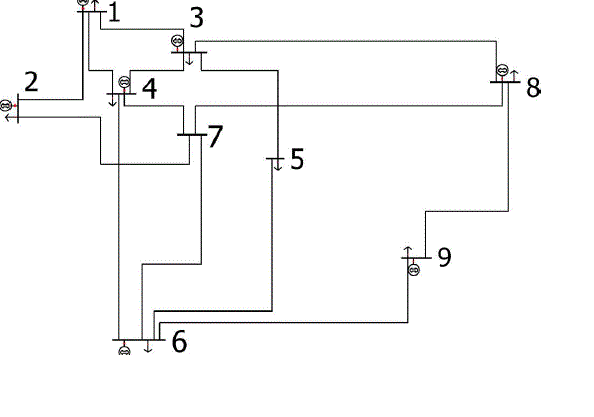
In an IEEE 118-bus system in [13], the flow limits of some lines are modified to create congestion profiles. At peak periods, two lines (Lines 37 and 38) can be congested. A similar procedure described in Section 2.1 yields the nine groups listed in Table 1,Fig. 1 illustrates the reduced network resulting from the procedure and a reduced network is formed based on the reduction algorithm in [12] is shown in fig. 2.
AC OPF studies for various load profiles are performed on the original and the reduced networks to compare the results. Various loads are simulated to find different congestion profiles.

CONCLUSION
For a large-scale power system, it is practically infeasible to find an optimal solution for power system planning. Recent development of network reduction allows precise modelling with a manageable computation expense. However, a proper assignment for the flow limits is missing, which is necessary for an OPF study. In this paper, an algorithm to find a proper group is proposed to assign for network reduction. The reduced network based on this group shows the same congestion profile as the original network in the OPF studies. Another advantage is that the flow limits of the aggregated lines that are not congested do not need to be assigned precisely. As a result, along with the network reduction algorithm, it provides a concise and precise representation of the transmission network for a power flow study. Therefore, this method can be used in a large system OPF.

Tables at a glance
Table icon Table icon Table icon
Table 1 Table 2 Table 3
 

Figures at a glance
Figure 1 Figure 2
Figure 1 Figure 2
 

References