INTRODUCTION
|
| Braking forms an important part of motion of any automobile or locomotive. Effective braking ensures the safety of the passengers and goods an automobile or a locomotive is carrying. Hence, new and effective braking techniques are required which increase the efficiency of the existing braking system by either replacing the older systems or by providing an auxiliary support whenever required. The main advantage of eddy current brakes lies over the fact that, more the relative motion between the metal and the magnetic source, more would be the braking force observed by the metal disc. Owing to their efficiency at very high speeds these brakes are used in high speed locomotives and their scope can be further increased to high performance/racing automobiles. Another important advantage is that it has no loses due to friction and thus improves the overall efficiency of the system. Thus, it is important to understand the various parameters that affect the braking force. |
BACKGROUND
|
| Current is induced when a conductor is introduced in a variable magnetic flux. This can be achieved by either exerting a time varying magnetic field over a static conductor or a static magnetic field over a moving conductor. In Eddy current braking system, a conducting disc is rotated in the air gap of the magnetic field produced by a permanent magnet or an electromagnet. Using electromagnets is a much efficient method since; the setup can be activated as per requirement. When the disc rotates in the magnetic field, eddy currents are induced into the conductor in such a manner that they oppose the cause producing it. As a result of the interaction between the magnetic field produced by the induced eddy currents and the magnetic field of the electromagnet, a braking force is experienced which causes braking or retardation of the disc. This braking force is dependent upon the velocity of rotating disc. The braking force increases as the velocity of disc increases. |
| When the metal plate enters the magnetic field, a Lorentz force, |
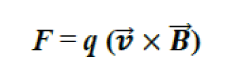 |
| The force experienced by the electron in the disc causes induced current which in such a way that it opposes the cause producing it. Thus, induced current flows in closed paths. Certain papers [2] mention about the proposed models and the equations regarding the eddy current braking. They propose W.R. Smythe?s Model, D.Schieber?s Model and J.H. Wouterse?s Model. |
| The former two propose valid results at low speeds whereas the third model is acceptable at high speed ranges also. It states that at low speed: |
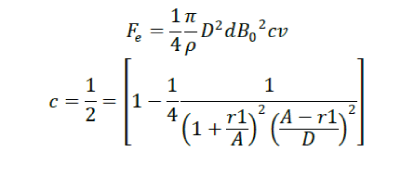 |
| At high speeds the braking force is : |
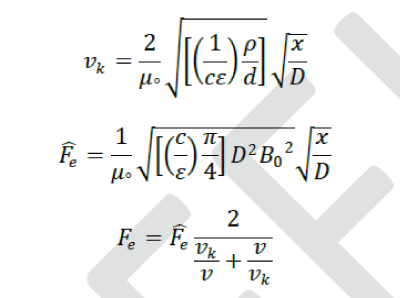 |
| The list of various symbols used is given in table 1: |
OBSERVATIONS
|
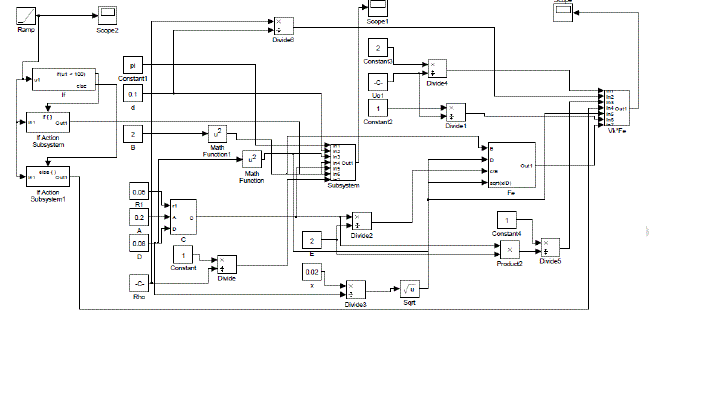
| The SIMULINK model is modeled using the above mentioned equation of "Fe " at both high speed and low speed. In order to determine the dependency of the braking torque, Fe , over a particular parameter, that parameter is varied as a Ramp signal keeping the other parameters constant. Through this we generate a time varying signal of the parameter under consideration. For example, if the dependency of braking torque over velocity of disc is to be established then the velocity of disc is fed as a Ramp signal varying with time of positive slope. Results can be obtained with any time varying signal of any slope, the author chooses time varying ramp signals. The basic SIMULINK model would look as following : |
Effect of change in velocity, v:
|
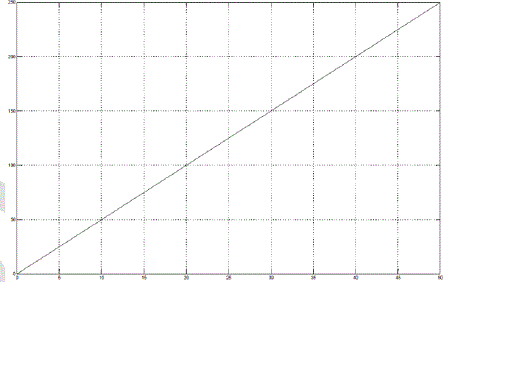
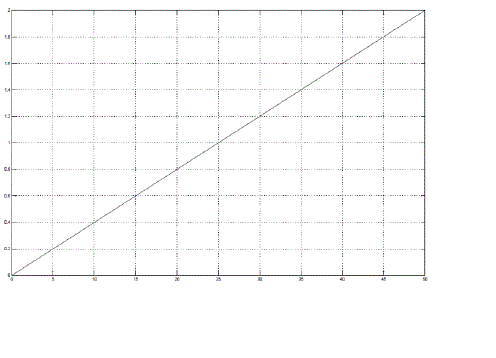
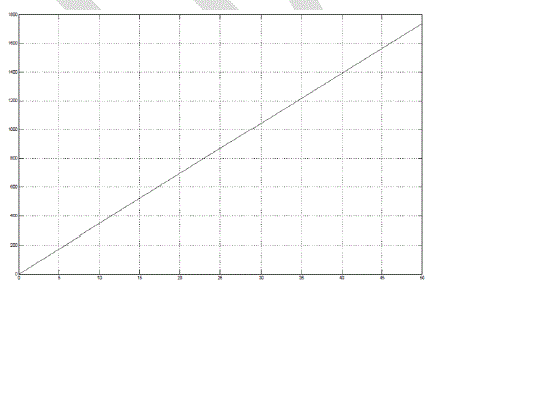
| In Fig 2, The speed is varied from 0-250 m/s i.e., 0-900km/hr. The following graph is obtained with Velocity on Yaxis and time on X-axis. A ramp Signal with slope 5 is used to provide velocity varying with time. The highest speed being 250m/s. |
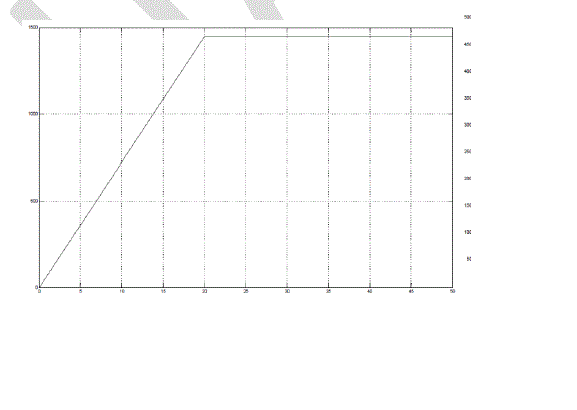
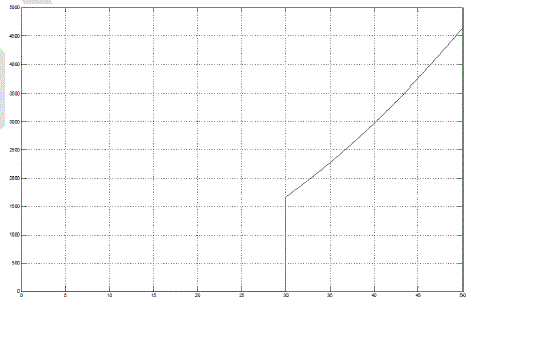
| In Fig 3, It can be clearly observed that, as the speed increases the braking torque (on Y-axis) also increases. At High Speed i.e., greater than 100 m/s the modeling is carried out according to the equation of braking force at high speeds. In Fig. 4, As observed, it can be concluded that the braking torque increases as velocity increases and hence, the braking torque stops acting when the velocity of the disc equals to zero. The reason of the trends observed in the above to graph is because, as stated by Lorentz law, mentioned above, as the relative velocity increases the magnitude of eddy current induced in disc increases which causes, and thus the induced eddy currents would try to oppose the cause producing it and hence higher value of braking torque is obtained. braking torque is directly proportional to the relative velocity of the source to the rotating metal. As the relative velocity between then increases, more braking force would be generated. This particular reason aids Eddy current brakes to be used in at High Speed applications as the high magnitude of braking force can be generated. |
Effect of change in Magnetic Field, Bo:
|
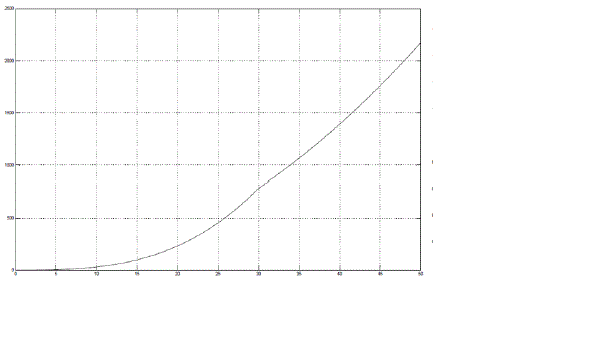
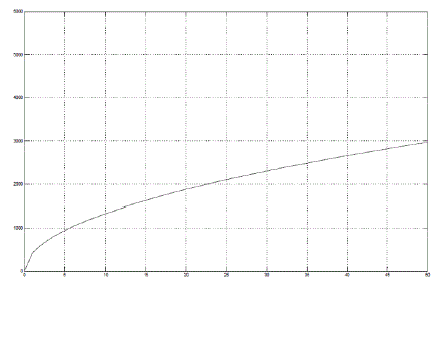
| In fig 4, the Magnetic field is increased from 0-2T, then its effect on the braking torque can be observed in Figure 5 and figure 6 for low speeds and high speeds respectively. The trend observed in both Fig 5 and Fig 6, indicates that the observed braking force increases as the magnitude of Magnetic Field increases. Since, the braking force increases, thus the brakes would work more over the wheel to stop its rotation and reduce its speed efficiently and much faster than the conventional braking system. The reason for the trends obtained in Fig 5 and Fig 6 can also be explained by Lorentz law. Since, eddy currents induced also depend upon the magnetic field of the source producing it. As the magnetic field increases so will the eddy currents induced and hence, the increased magnitude of eddy currents would oppose the cause producing it. The interaction of the two magnetic fields of the source and that produced by induced eddy current would generate the braking torque in a value proportional to the change in magnetic field. Thus, increase in magnetic field causes increase in braking force. |
| In Fig 4, a time varying magnetic field can be obtained by providing a ramp signal of slope 0.04 hence, generating values from 0-2T. |
Effect of increasing width of Air-Gap, x :
|
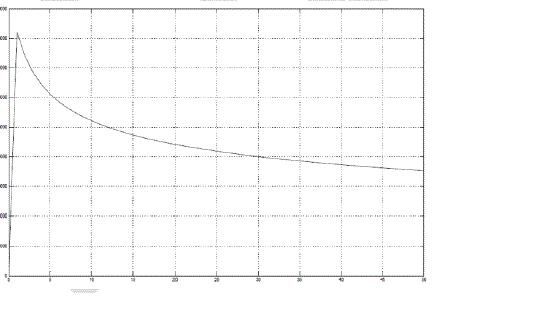
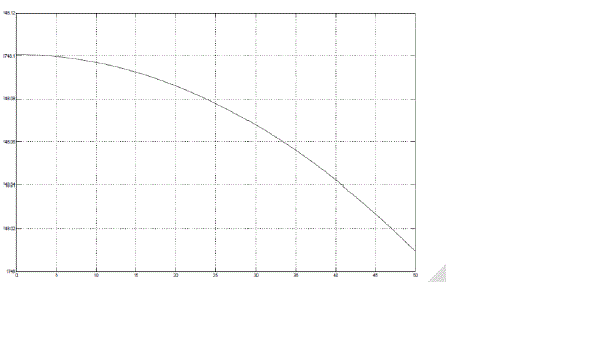
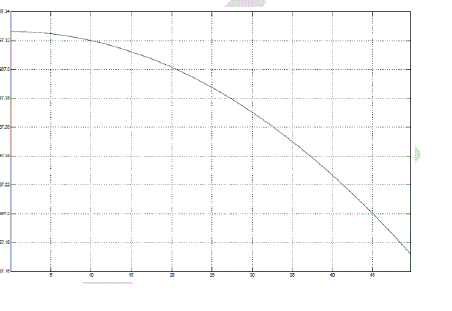
| If the air gap between the poles of magnet is increased with time then, at low Speed, the change in air gap does not have much effect on the braking force as observed in Fig 7. But, at high speed, initially on increasing the air gap the braking force increases and after a particular point the braking force decreases as in fig 8. At this point of maxima, the strength of the dipole formed would be maximum and hence, maximum braking force is obtained and such a position can be the optimum braking position at high speeds. The trend observed in Fig 7 can be explained as, at lower speeds since, the change in air-gap has negligible effect on the magnitude of magnetic field between the poles of the electromagnet. Thus, the magnitude of braking force obtained is relatively constant. The trend in fig 8 is a result of obtaining increasing air gap as a function of time. As the poles are moved at a distance which is greater than the thickness of the disc apart from each other the effective magnetic field decreases. This is because the effective magnetic field is an inversely proportional function to the distance between the poles. As the distance increases, the effective magnetic field decreases and since, the braking force is proportional to changes in magnetic field strength, the braking force also decreases. |
Effect of increase in thickness of Disc, d :
|
| If thickness of Disc, “d” is increased with time, then at low speeds, as observed in Fig 9, braking force (Y-axis) increases with the increasing thickness of the disc. Also similarly at high speeds, as in Fig 10, braking force (Y-axis) increases with increasing thickness of the disc. The trends observed in Fig 10, can be explained as by increasing the thickness the air gap decreases and as a result the braking force increases as explained in the previous case. At lower speeds for Fig 9, the function of braking force is proportional to thickness of disc and as a result the braking force increases when the thickness increases. |
Effect of increase in position of centre of pole from centre of disc, r1:
|
| Centre of pole refers to the distance of point where, line joining the centers of both the poles and the surface of the disc meet, measured along the surface of the disc. As observed in fig 11 and fig 12, If this distance is increased, then the braking force would decrease. This is because as we move away from the centre the effect of magnetic field produced by the eddy current does not provide the same braking force as it did closer to the centre. This is because the effective field at any point producing the eddy current depends inversely over r1. As r1 increases magnitude of effective magnetic field decreases and thus braking force decreases. Braking force would be maximum at the centre and least at the edges. |
Effect of increase in Diameter of pole which increases the area of magnetism over the disc, D :
|
| If the diameter of soft iron pole is increased or the diameter of the area at which the magnetic source acts is increased then the braking force also increases as can be observed from both fig 13 and fig 14. This is because as the diameter of pole is increased the effective area where the eddy currents are produced increases. This causes an increase in magnitude of the eddy currents, which produce magnetic field in the direction opposite to the cause producing the eddy current. As the area is increased, magnitude of eddy current produced would increase and thus, increasing the force in direction opposite to that of the source producing the eddy currents would be produced. |
ADVANTAGES AND DISADVATAGES
|
Advantages:
|
| Eddy current brakes depend upon the velocity the disc. Braking Force is more for higher velocity and reduces as velocity is reduced and stops acting if the disc stops rotating. Also, Frictional loses are greatly reduced since, it has no moving or sliding parts. This even reduces cost of maintenance. It can be used in addition to the existing brake system as an auxiliary brakes to provide efficient braking at very high speeds. |
Disadvantages :
|
| Since, it is dependent upon velocity of the disc hence, it cannot hold the disc at rest, as opposed to the holding force provided by the static friction of conventional brakes. Also, the braking force decreases as the speed decreases and hence, conventional brakes are required if more braking force is required. Maybe costly if operated for low speed applications. |
PERFORMANCE EFFECTS ON AN EXISTING SYSTEM
|
| Based on the observations above, it can be observed that if the above mentioned parameters are changed their effects would be observed over the existing system with which they are working upon. If the magnitude of magnetic field is increased or decreased then the braking force would increase or decrease respectively causing much faster and efficient braking. Also the distance between the pole plays a major role at high speeds. The poles should be at a distance of the optimum braking point, because of which the most efficient braking is obtained. Also, thickness of the disc, and positioning of the poles play another important role. Altering any of the factor would alter the performance of the brakes and hence, alter its efficiency. Also all parameters should parameters should be designed in such a way that braking force doesn?t reach a point where jerks are observed while braking and sliding of disc is not observed. The applications include being used in High speed trains and high performance lifts. Hence, all the parameters needs to be designed keeping the above observed trends in consideration. Also, eddy current braking system can act as a very efficient braking system at high speeds and thus, be used as auxiliary brakes for many high speed applications along with the conventional mechanical brakes being used. Since, both the brakes would act on the wheel or the shaft responsible for braking, the effective time where the brakes act can be reduced and hence, the automobile or locomotive be stopped in a much lesser time and distance. |
CONCLUSION
|
| Thus, the eddy current brakes are modeled and the various factors and parameters affecting the efficient braking are observed. The above analysis could be reviewed while designing of eddy current brakes. |
Tables at a glance
|
 |
| Table 1 |
|
| |
Figures at a glance
|
 |
 |
 |
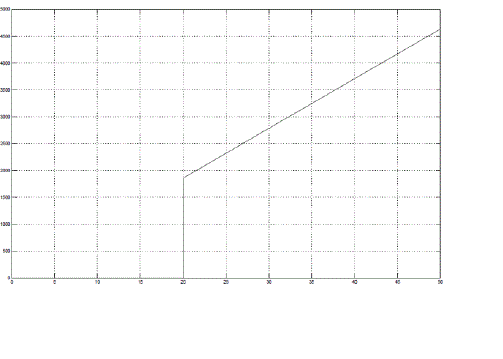 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
 |
 |
 |
 |
 |
| Figure 6 |
Figure 7 |
Figure 8 |
Figure 9 |
Figure 10 |
 |
 |
 |
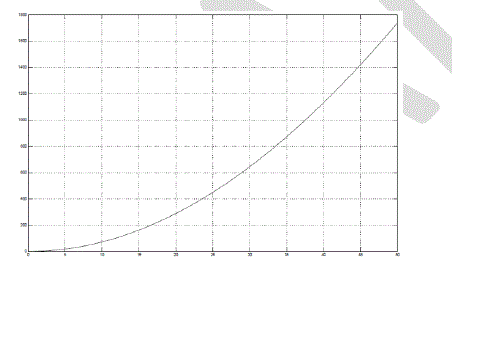 |
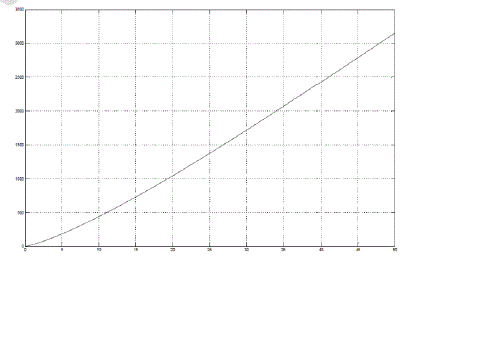 |
| Figure 11 |
Figure 12 |
Figure 13 |
Figure 14 |
Figure 15 |
|
| |
References
|
- Manuel I Gonz´alez, “Experiments with Eddy Currents: the Eddy Brakes”, Institute of Physics Publishing, Vol. 25 , pp 463-468, 2004.
- Der-Ming Ma, Jaw- Kuen Shiau, “The design of Eddy-current Magnet Brakes”, Transactions of Canadian Society for Mechanical Engineering, Vol 35, pp 19-37, 2011.
- Jure Hribar, “Magnetic Braking”, Journal of mathematics and physics - University of Ljubljana, Vol 5, pp 26-39- 2008
- Marshall S V and Skitek G G, “Electromagnetic Concepts and Applications” 3rd edition (Englewood Cliffs, NJ: Prentice-Hall) pp 298–9,1990.
- El-Hawary, “Electrical Energy Systems”, Boca Raton, FL: CRC Press, pp 36–40, 2000
- Gagarin, G., Kroger, U. And Saunweber, E., „„Eddy-current magnetic track brakes for high speed trains,?? Joint ASME/IEEE/AAR RailroadConference, pp. 95–99, 1987
- Mcconnell, H.M., „„Eddy-current phenomena in ferromagnetic material,?? AIEE Transactions, Vol. 73, part I, pp. 226–234, July, 1954.
- Sears F W, Zemansky M W, Young H D and Freedman R A “ F´?sica Universitaria, Novena Edici”, vol 2 (Mexico: Addison-Wesley), pp 957–8,1999
- Thomas D. Rossing and John R. Hull, “Magnetic Levitation”, Vol 2, The Physics Teacher, 552-561,1991.
- Tipler P, “Physics for Scientists and Engineers” 4th edn (New York: Freeman),pp 938–9,1999.
- Serway R and Beichner R “Physics for Scientists and Engineers with Modern Pysics”, 5th edn (Fort Worth:Saunders) pp 997–9, 2000
- http://inventors.about.com/library/inventors/blrailroad3.html
- Electric Pulse magnetic Braking using Mechatronics
- Iniguez J, Raposo V, Hernandez-Lopez A, Flores A G and Zazo M, “Study of the conductivity of a metallic tube by analysing the damped fall of a magnet” Eur. J. Phys., Vol25, pp-593–604, 2004
- Levin Y, da Silveira F L and Rizzato F B, “Electromagnetic braking: a simple quantitative model”, Am. Journal of Phys. Vol 74, pp 815–7, 2006
|