Keywords
|
| MP3, Audio water marking, DD-DWT. |
INTRODUCTION
|
| It is more important to secure the data against theft, loss and damage along with the criminal activity to hack. If we want to send a sensitive message is to be delivered to a destination, authentication and confidentiality are required. Security for electronic documents is very important issue. Digital watermarking is a very important technique in which pieces of information into a digital media for protecting it against copyright and other unauthorized applications. This has to protect the audio file from illegal copying. A lot of works has been done on digital watermarking of various media such as image and video, but this particular review will focus on digital watermarking of audio file. Digital Audio files are particularly the most abused for copyright infringements because they can be downloaded and copied with easily.. Audio watermarks are special signals embedded into digital audio. These signals are detected and extracted by detection process and by decoding. This hiding schemes rely on the imperfection of auditory system of the human beings. However, human ear is sensible to than other sensory motors. Thus, the design of good audio watermarking schemes are difficult. But now there has been a proposed solutions to this problem of copyright infringement. The use of various types of watermarks has been achieved. |
| The authors proposed that the use of data such as information, text or images are embedded in the audio file such that any of such audio file could be processed and analyzed for possible recovery of the hidden data. But some other authors use pseudorandom number generators for watermark generation while other use chaotic watermarks for protection of audio files combined with various techniques. |
| Till now a lot of number of techniques and methods are used for copyright protection. But the efforts for real time application has been low. So there is a need for a way or technique to protect this work against abuse, creating a need for critically reviewing the work done so far to know how it can meet this need at the earliest time. This paper will present a currently a audio hidden technique against the various properties of the watermark which satisfy the best result to attain the factors against the real improvement of the watermarking technique. |
| The Digital audio watermarking has provide a efficient solutions for copyright protection of digital media by inserting a hidden data signal in the original audio signal, to provide a deal of attention in the literature. The main essential requirement of digital audio watermarking signals are imperceptibility, robustness and data capacity. Moreover, the watermark must be inaudible within the original audio data to maintain audio quality and robust to signal distortions applied to the host data. The properties of a digital watermark depend on the use case in which it is applied. Finally, to prove its ownership the watermark is easy to extract. To overcome this problems, achieving a new watermarking schemes is a very challenging job. Different watermarking techniques having more complications have been proposed. In a robust watermarking scheme to different attacks is proposed but with a limited transmission bit rate. To increase the bit rate, watermarked schemes having wavelets domain is proposed. A limit of this approach is that the basis functions are fixed, but for all real signals it can not match necessarily. |
| The dual tree concept can be extended to other types of DWTs. Digital audio watermarking has received a attention in the literature to copyright protection of digital media thus providing a effective solution by inserting a watermark in the original audio signal.. |
EXISTING METHOD
|
| Different watermarking strategies of fluctuating complexities have been proposed . In a strong watermarking plan to distinctive assaults is proposed however with a restricted transmission bit rate. To enhance the bit rate, watermarked plans performed in the wavelets space have been proposed. A cutoff of wavelet methodology is that the essential capacities are altered, and along these lines they don't fundamentally match all genuine signs. |
AUDIO WATERMARKING TECHNIQUES
|
| In this segment, the five most well known systems for advanced sound watermarking are looked into. Particularly, the distinctive procedures compare to the techniques for uniting (or embeddings) the spread information and the watermark design into a solitary sign. |
A. Spread spectrum watermarking
|
| Spread-spectrum audio data hidden scheme is the correlation method which embeds pseudorandom sequence and extract hidden data by calculating correlation between pseudo-random noise sequence and watermarked audio signal. Spread spectrum techniques for watermarking is to get information theory from the communications. The narrowband signal (the watermark) is embedded into a wide-band audio-channel. The characteristics of both audio signal A and watermark W seem to suit the model perfectly. In addition, spread spectrum techniques helps the probability to protect hidden data privacy by using a secret logic key to regulate the pseudorandom sequence generator. Spread spectrum techniques admit the frequency bands to match before embedding the message. So the spread spectrum techniques are i only for secure communication but also for watermarking scheme as well. There are two basic approaches to spread spectrum techniques: direct sequence and frequency hopping. The two approaches are to spread the watermark data across a large frequency band, almost all the entire audible spectrum. |
B. Amplitude modification
|
| This technique, is also called as minimum critical bit (LSB) substitution. This is regular and simple to apply in both steganography and watermarking scheme as it exploits the quantization slip that typically gets from the undertaking of digitizing the sound sign. The data is encoded into the slightest noteworthy bits of the audio information. There are two methods for doing this: the lower request bits of the advanced sound sign can be completely substituted with a pseudorandom (PN) arrangement that contains the watermark message m, or the PN-grouping can be implanted into the lower request bit stream utilizing the yield of a capacity that produces the succession focused around both nth bit of watermark message and nth specimen of sound document. The real detriment of this system is its poor invulnerability to control. Encoded data can be obliterated by channel clamor, re-examining, and so forth., unless it is encoded utilizing excess strategies. To be hearty, these methods lessen the information rate, regularly by one to two requests of greatness. Besides, so as to make the watermark more strong against confined separating, a pseudorandom number generator can be utilized to spread the message over the spread in an arbitrary way. |
C. Replica Method
|
| The original audio signal can also be used as data hiding information, The good example of this replica method is Echo hiding. Replica modulation embeds part of the original audio signal in frequency domain as a watermark. Thus, replica modulation embeds replica, i.e., a properly modulated original signal, as a watermark. It also calculate the correlation. Detector can also generate The replica is also generated by the detector from the watermarked audio. |
D. Dither watermarking
|
| Dither is a clamor flag that is added to the info sound sign to give better testing of that enter when important not digitizing the sign (4). As an issue, bending is basically wiped out, at the expense of an expanded commotion floor. To actualize dithering, a clamor sign is added to the data sound sign with a known likelihood dissemination, for example, Gaussian or triangular. In the specific instance of dithering for watermark installing, the watermark is utilized to regulate the dither signal. The host sign (or unique sound document) is quantized utilizing a related dither quantizer. This method is known as quantization list regulation (QIM) . A graphical perspective of this method. Here, the focuses checked with X's and O's have a place with two diverse quantizer, each with a related record; that is, every one installing an alternate worth. The separation dmin can be utilized as a casual measure of vigor, while the extent of the quantization cells (one is demonstrated in the figure) measures the mutilation on the sound document. |
PROPOSED METHOD
|
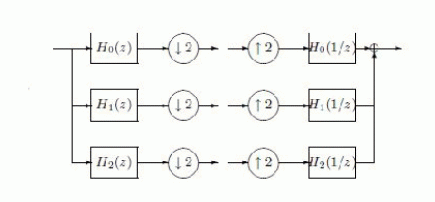
| Other than the sampled transforms the signal processing applications like de-noising and over-complete transforms offer a better trade off between performance and complexity. A distinguished member of this family is over complete discrete wavelet transforms ( DWT) is the double density (DD) DWT, based on the filter bank shown in Figure 1. The input audio signal is separated in to three channels, each decreased by a factor of two. The signal on the first channel is analysed by an identical filter bank etc. The DD-DWT is expansive with a factor of two, compared to the critically sampled DWT. A dual tree (DT) is formed by two wavelet transforms processing a same single input audio signal that satisfy a certain relationship. Both the wavelets can form a approximate Hilbert transform. The DT-DWT we can consider a nearly shift invariance and directional selectivity in high amplitudes. |
| If we can take two filter banks with the modal from Figure 1, the first(the primal) defined by filters H0(z), H1(z) and H2(z), the second( the dual) are considered by filters K0(z), K1(z) and K2(z). Let ψh ,i(t) and ψg ,i(t), i = 1, 2, be the wavelets generated by the filters H0(z), Hi(z) and K0(z), Ki(z), respectively. The two DD-DWTs form a dual-tree if ψg,i(t) and ψh,i(t) form a Hilbert transform. Equivalently, the complex wavelet ψi(t) = ψh,i(t) + jψg,i(t) is approximately analytic and so its spectrum i(t), ∈ R, is approximately zero for negative frequencies. |
| The design of dual-tree DD-DWT was presented with an algorithm, using allpass. An approximate a half-sample delay is produced by the system. In this we consider another approach. We assume that the primal DD-DWT is given: the FIR filters H0(z), H1(z), H2(z) are known. We initialize semi-definite programming (SDP) solutions which allows to compute FIR filters K0(z), K1(z), K2(z) that form a relatively good dual filter bank. These filters are ∞- norm approximations of z−1/2H0(z) and of the Hilbert transforms of z1/2H1(z), z1/2H2(z), respectively. However, these filters do not respect exactly the perfect reconstruction (PR) conditions required for the DD filter bank, namely P2 |
| i=0, K i(z) Ki(z−1) = 2 P2 |
| i=0, K i(z) Ki(−z−1) = 0 |
| As these situations are not visible, we must implement the filters K0(z), K1(z), K2(z) by optimizing them. .Both the DD-DWT and the dual-tree DWT have their own properties and advantages, and as such, it was only natural to combine the two into one transform called the double-density complex (or DD- dual-tree) DWT. To combine the characteristics of both the DD and dual-tree DWTs we ensure that: (1) Out of four wavelets one pair is offset from the other pair of wavelets so that the integer translates of one wavelet pair fall midway between the integer translates of the other pair , one wavelet pair is designed to be approximate Hilbert transforms of the other pair of wavelets . By doing this, we are then able to use the DD complex wavelet transform to implement complex & directional wavelet transforms. |
| In order to improve the DD dual-tree DWT, we have to design an filter bank model (one that combines the properties of the DD and dual-tree DWTs). We have seen what type of filter bank modal is associated with the double-density DWT in the previous sections (mainly that it is composed of one lowpass scaling filter and two highpass wavelet filters), so we will now turn to the properties of the dual-tree DWT. The dual-tree DWT is based primarily on concatenating two critically sampled DWTs. We do this by constructing a filter bank that performs multiple iterations in parallel. |
EXPERIMENTAL RESULTS
|
CONCLUSION
|
| The digital audio watermarking techniques are proved to be a valuable for copyright control of digital material. The studies on audio watermarking are far less than that of image watermarking or video watermarking. However, during the last ten years audio watermarking studies have also increased a lot. contribution has brought a progress of audio watermarking technologies. This paper analysed those papers and presented some of the important techniques used for digital audio watermarking. The contribution of this paper is twofold. We presented the required algorithm to compute the second filter bank of a DD-DWT. The Designed examples have shown the viability of this approach. |
Figures at a glance
|
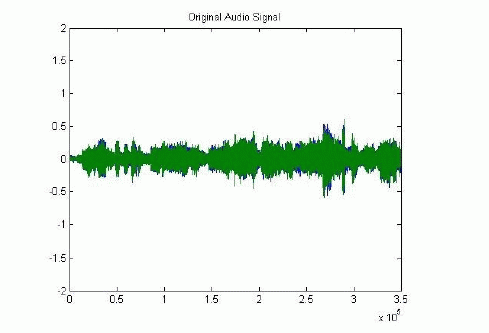
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
 |
 |
 |
| Figure 4 |
Figure 5 |
Figure 6 |
|
| |
References
|
- I. J. Cox and M. L. Miller, “The first 50 years of electronic watermarking,” J. Appl. Signal Process., vol. 2, pp. 126–132, 2002.
- M. D. Swanson, B. Zhu, and A. H. Tewfik, “Robust audio watermarking using perceptual masking,” Signal Process., vol. 66, no. 3, pp. 337–355,1998.
- S. Wu, J. Huang, D. Huang, and Y. Q. Shi, “Efficiently self-synchronized audio watermarking for assured audio data transmission,” IEEE Trans.Broadcasting, vol. 51, no. 1, pp. 69–76, Mar. 2005.
- V. Bhat, K. I. Sengupta, and A. Das, “An adaptive audio watermarking based on the singular value decomposition in the wavelet domain,” DigitalSignal Process, vol. 2010, no. 20, pp. 1547–1558, 2010.
- D. Kiroveski and S. Malvar, “Robust spread-spectrum audio watermarking,” in Proc. ICASSP, 2001, pp. 1345–1348.
- N. E. Huang et al., “Theempirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis,” Proc. R. Soc., vol. 454, no. 1971, pp.903–995, 1998.
- K. Khaldi, A. O. Boudraa, M. Turki, T. Chonavel, and I. Samaali, “Audio encoding based on the EMD,” in Proc. EUSIPCO, 2009.
- K. Khaldi and A. O. Boudraa, “On signals compression by EMD,” Electron.Lett., vol. 48, no. 21, pp. 1329–1331, 2012.
- K. Khaldi, M. T.-H. Alouane, and A. O. Boudraa, “Voiced speech enhancement based on adaptive filtering of selected intrinsic mode functions,”J. Adv. in Adapt.Data Anal., vol. 2, no. 1, pp. 65–80, 2010.
- I.W. Selesnick, “The Double-Density Dual-Tree DWT,” IEEE Trans. Signal Processing, vol. 52, no. 5, pp. 1304–1314,May 2004.
- N.G. Kingsbury, “Complex wavelets for shift invariant analysis and filtering of signals,” J. Applied and Computational Harmonic Analysis, vol.10, no. 3, pp. 234–253,May 2001.
- I.W. Selesnick, R.G. Baraniuk, and N.G. Kingsbury, “The Dual-Tree ComplexWavelet Transform,” IEEE Signal Proc.Magazine, vol. 22, no. 6,pp. 123– 151, Nov. 2005.
- I.W. Selesnick, “Hilbert Transform Pairs of Wavelet Bases,” IEEE Signal Proc. Letters, vol. 8, no. 6, pp. 170–173, June 2001.
- R. Yu and H. Ozkaramanli, “Hilbert Transform Pairs of Orthogonal Wavelet Bases: Necessary and Sufficient Conditions,” IEEE Trans. SignalProcessing, vol. 53, no. 12, pp. 4723–4725, Dec. 2005.
- B. Dumitrescu, “SDP Approximation of a Fractional Delay and the Design of Dual-Tree Complex Wavelet Transform,” IEEE Trans. SignalProc., 2008, to appear.
- B. Dumitrescu, Positive trigonometric polynomials and signal processing applications, Springer, 2007.
|