ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
R.Prasanna1, Abraham Mathew2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
A QR (Quick Response) code is a special type of barcode that can encode information like numbers, letters, and any other characters. The capacity of a given QR code depends on the version and error correction level, as well as on the type of data that you are encoding. Here the color QR code framework for mobile phone applications by exploiting the spectral diversity afforded by the cyan (C), magenta (M), and yellow (Y) print colorant channels commonly used for color printing and the complementary red (R), green (G), and blue (B) channels, respectively, used for capturing color images. Specifically, the exploitation of this spectral diversity to realize a three-fold increase in the data rate by encoding independent data in the C, M, and Y print colorant channels and decoding the data from the complementary R, G, and B channels. In most cases Reed-Solomon error correction codes will be used for generating error correction codeword’s. Here there is a add bit based channel code is also used along with block based reed Solomon code to increase the interference cancellation rate. Experimental results will show that the proposed framework successfully overcomes both single and burst errors and also providing a low bit error rate and a high decoding rate for each of the colorant channels when used with a corresponding error correction scheme.Colorant channels that provide three different primary colors at RGB mode which select the code that convert the actual value to the proposed frame work that calculates interference cancellation rate. Reed Solomon error correction code is used here which reduces the interference.
\r\n Keywords\r\n | \r\n
| 2Dbar codes,Aztec codes,color bar codes, interference cancellation,quick response (QR) codes. | \r\n
\r\n INTRODUCTION\r\n | \r\n
| As the significant increase of mobile device users, more wireless information services and mobile commerce applications are needed. In the past decade, various barcodes have been used as a very effective means in many traditional e-commerce systems, supply chain management, retail sale-and-buy, as well as tracking and monitoring of products and goods. Today, many people believes that digital barcodes provides an effective means for mobile commerce application systems due to the following reasons: By Using digital barcodes provides a simple and inexpensive method to present diverse commerce data in electronic commerce and m-commerce, including product id and the detailed product information, advertisements, and purchasing and payment information. As more mobile digital cameras are deployed on mobile devices, using digital barcodes is becoming an effective way to reduce the mobile inputs from mobile users. Therefore, mobile user experience can be improved and enriched. To meet the increasing needs of mobile-based barcode applications in m-commerce, more research work and technology study are needed to understand 2DBarcodes, required supporting technologies, standards. | \r\n
| The concept of barcodes appeared decades ago. Traditionally, the barcodes stored data in the form of parallel lines in different widths, and they are known as 1D barcodes, and could only encode numbers [10]. About 30 years ago, the first linear barcodes were used for railway transportation and tracking of the goods in USA. Since then, barcodes have been used almost everywhere, including manufacturing, postal, transportation, government, health care, retail business, trade show, and automotive business. Barcodes, as machine-readable representation of information in a visual format, can be easily stored, transferred, processed, and validated. | \r\n
 | \r\n
\r\n II.2D QR CODES AND COLOR CODES\r\n | \r\n
| QR Code is a form of 2D bar codes. It was developed by Denso-Wave, a Japanese automatic data capture equipment company (Denso, 2009), in 1994. “QR” stands for “Quick Response.” It is readable by moderately equipped mobile phones with cameras and QR scanners. Information such as URL, SMS, contact information and plain text can be embedded into the two dimensional matrix. | \r\n
| With smart phones, we can visit the Website linked by the URL quickly, we can send the SMS message directly or we can save the contact information onto the address book easily. This format of 2D bar codes is so popular in Japan and emerges gradually around the world because (a) the patent right owned by Denso Wave is not exercised (Denso, 2010a), (b) its specification is disclosed to the public by the company so as the specifications, ISO/IEC 18004:2000&2006 (International Organization for Standardization) and JIS X 0510 (Japanese Industrial Standards), can be formed (ISO, 2010; JISC, 2010), and (c) it has a large data capacity in a small printout size and high speed scan utilities via mobile devices are readily available. QR code is capable of holding 7,089 numeric characters, 4,296 alphanumeric characters, 2,953 binary bytes, 1,817 Kanji characters or a mixture of them. The data capacity is much higher than other 2D codes such as PDF417, Data Matrix and Maxi Code (Denso, 2010b). It stores information in both vertical and horizontal directions. A QR code can be read from any direction in 360° through position detection patterns located at the three corners. QR code can be read even it is somewhat distorted by either being tilted or on a curved surface by alignment patterns and timing patterns. The error correction capability against dirt and damage can be up to 30%. A linking functionality is possible for a QR code to be represented by up to 16 QR codes at maximum so that a small printing space is possible. The size of a QR code can vary from 21x21 cells to 177x177 cells by 4 cell-increments in both horizontal and vertical direction. | \r\n
| Data can be easily encrypted in a QR code to provide a confidentiality of information embedded in the code. It can also handle various languages. For examples, there are a number of standards adopted by Asian countries like GB/T 18284 by Chinese National Standard in 2000, KS-X ISO/IEC 18004 by Korean National Standard in 2002, and TCVN7322 by Vietnam National Standard in 2003. | \r\n
\r\n III.FORWARD ERROR CORRECTION AND ECC\r\n | \r\n
| An error-correcting code (ECC) or forward error correction (FEC) code is a system of adding redundant data, or parity data, to a message, such that it can be recovered by a receiver even when a number of errors (up to the capability of the code being used) were introduced, either during the process of transmission, or on storage. Since the receiver does not have to ask the sender for retransmission of the data, a back-channel is not required in forward error correction, and it is therefore suitable for simplex communication such as broadcasting. Errorcorrecting codes are frequently used in lower-layer communication, as well as for reliable storage in media such as CDs, DVDs, hard disks, and RAM. Errorcorrecting codes are usually distinguished between convolutional codes and block codes: | \r\n
| ïÃâ÷ Convolutional codes are processed on a bit-bybit basis. They are particularly suitable for implementation in hardware, and the Viterbi decoder allows optimal decoding. | \r\n
| ïÃâ÷ Block codes are processed on a block-by-block basis. Early examples of block codes are repetition codes, Hamming codes and multidimensional parity-check codes. They were followed by a number of efficient codes, Reed- Solomon codes being the most notable due to their current widespread use. Turbo codes and low-density parity-check codes (LDPC) are relatively new constructions that can provide almost optimal efficiency. | \r\n
| Shannon''s theorem is an important theorem in forward error correction, and describes the maximum information rate at which reliable communication is possible over a channel that has a certain error probability or signal-to-noise ratio (SNR). This strict upper limit is expressed in terms of the channel capacity. More specifically, the theorem says that there exist codes such that with increasing encoding length the probability of error on a discrete memory-less channel can be made arbitrarily small, provided that the code rate is smaller than the channel capacity. The code rate is defined as the fraction k/n of k source symbols and n encoded symbols. The actual maximum code rate allowed depends on the error-correcting code used, and may be lower. This is because Shannon''s proof was only of existential nature, and did not show how to construct codes which are both optimal and have efficient encoding and decoding algorithms. | \r\n
| Here we propose a new approach to design Viterbi decoder using finite state machines instead of using shift registers and adders. As FSM reduces both static and dynamic power. The Viterbi algorithm is the optimal solution for the convolutional codes [1][2]. The nonlinear and recursive nature limits the maximum achievable throughput rate. The most common solution to develop a high throughput Viterbi decoder is fully parallel approach, where ACS units are assigned to each state with high radix structure[3]. However, as the constraint length rises, the hardware complexity increases exponentially, and so does the power consumption. The first problem arised is the large number of ACS operations. The 2K_1 ACS operations are required for each iteration, where K is the constraint length. The second problem is that implementing a high speed trace-back unit is more difficult than that based on the register exchange method [4]. The trace-back algorithm for survivor memory management has been proposed in [5] and [6]. The kpointer algorithm divides the memory into banks, and accesses them concurrently to achieve the demanded data bandwidth. Another approach is one-pointer algorithm which requires higher memory access rate. Both of the methods will consume much power due to large number of memory access operations. And,power consumption is a key factor in mobile or battery-powered systems. This paper proposes a modified traceback scheme that reduces the memory access based on the path merging property [2], which will be discussed with mathametical fomulation in section 2. Section 3 shows the proposed architecture including the performance evaluation of soft decision decoding, high speed radix-4 ACS structure, and the cache based survivor memory design. | \r\n
| Forward error correction (FEC) or channel coding is a technique used for controlling errors in data transmission over unreliable or noisy communication channels. The central idea is the sender encodes their message in a redundant way by using an error-correcting code (ECC). The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code. The redundancy allows the receiver to detect a limited number of errors that may occur anywhere in the message, and often to correct these errors without retransmission. FEC gives the receiver the ability to correct errors without needing a reverse channel to request retransmission of data, but at the cost of a fixed, higher forward channel bandwidth. FEC is therefore applied in situations where retransmissions are costly or impossible, such as when broadcasting to multiple receivers in multicast. FEC information is usually added to mass storage devices to enable recovery of corrupted data. | \r\n
| FEC processing in a receiver may be applied to a digital bit stream or in the demodulation of a digitally modulated carrier. For the latter, FEC is an integral part of the initial analog-to-digital conversion in the receiver. The Viterbi decoder implements a soft-decision algorithm to demodulate digital data from an analog signal corrupted by noise. Many FEC coders can also generate a bit-error rate (BER) signal which can be used as feedback to finetune the analog receiving electronics. The maximum fractions of errors or of missing bits that can be corrected is determined by the design of the FEC code, so different forward error correcting codes are suitable for different conditions. | \r\n
| A. Convolutional Coding | \r\n
| ïÃâ÷ The purpose of this tutorial is to introduce the reader to a forward error correction technique known as convolutional coding with Turbo decoding. | \r\n
| ïÃâ÷ Here we provide a detailed description of the algorithms for generating random binary data, convolutionally encoding the data, passing the encoded data through a noisy channel, quantizing the received channel symbols, and performing turbo decoding on the quantized channel symbols to recover the original binary data. | \r\n
| ïÃâ÷ The purpose of forward error correction (FEC) is to improve the capacity of a channel by adding some carefully designed redundant information to the data being transmitted through the channel. | \r\n
| ïÃâ÷ The process of adding this redundant information is known as channel coding. Convolutional coding and block coding are the two major forms of channel coding. | \r\n
| ïÃâ÷ Convolutional codes operate on serial data, one or a few bits at a time. Block codes operate on relatively large (typically, up to a couple of hundred bytes) message blocks. There are a variety of useful convolutional and block codes, and a variety of algorithms for decoding the received coded information sequences to recover the original data. The reader is advised to study the sources listed in the bibliography for a broader and deeper understanding of the digital communications and channel-coding field. | \r\n
| ïÃâ÷ Convolutional encoding with Viterbi decoding is a FEC technique that is particularly suited to a channel in which the transmitted signal is corrupted mainly by additive white gaussian noise (AWGN). You can think of AWGN as noise whose voltage distribution over time has characteristics that can be described using a Gaussian, or normal, statistical distribution, i.e. a bell curve. Error correction may generally be realized in two different ways: | \r\n
| ïÃâ÷ Automatic repeat request (ARQ) (sometimes also referred to as backward error correction): This is an error control technique whereby an error detection scheme is combined with requests for retransmission of erroneous data. Every block of data received is checked using the error detection code used, and if the check fails, retransmission of the data is requested – this may be done repeatedly, until the data can be verified. | \r\n
| ïÃâ÷ Forward error correction (FEC): The sender encodes the data using an error-correcting code (ECC) prior to transmission. The additional information (redundancy) added by the code is used by the receiver to recover the original data. In general, the reconstructed data is what is deemed the "most likely" original data. | \r\n
| ARQ and FEC may be combined, such that minor errors are corrected without retransmission, and major errors are corrected via a request for retransmission: this is called hybrid automatic repeat-request (HARQ). Error detection is most commonly realized using a suitable hash function (or checksum algorithm). A hash function adds a fixedlength tag to a message, which enables receivers to verify the delivered message by recomputing the tag and comparing it with the one provided. There exists a vast variety of different hash function designs. However, some are of particularly widespread use because of either their simplicity or their suitability for detecting certain kinds of errors (e.g., the cyclic redundancy check''s performance in detecting burst errors). | \r\n
| Random-error-correcting codes based on minimum distance coding can provide a suitable alternative to hash functions when a strict guarantee on the minimum number of errors to be detected is desired. Repetition codes, described below, are special cases of error-correcting codes: although rather inefficient, they find applications for both error correction and detection due to their simplicity. | \r\n
 | \r\n
\r\n IV.DETECTING SCHEMES\r\n | \r\n
\r\n A. Repetition codes\r\n | \r\n
| A repetition code is a coding scheme that repeats the bits across a channel to achieve error-free communication. Given a stream of data to be transmitted, the data is divided into blocks of bits. Each block is transmitted some predetermined number of times. For example, to send the bit pattern "1011", the four-bit block can be repeated three times, thus producing "1011 1011 1011". However, if this twelve-bit pattern was received as "1010 1011 1011" – where the first block is unlike the other two – it can be determined that an error has occurred. | \r\n
| Repetition codes are very inefficient, and can be susceptible to problems if the error occurs in exactly the same place for each group (e.g., "1010 1010 1010" in the previous example would be detected as correct). The advantage of repetition codes is that they are extremely simple, and are in fact used in some transmissions of numbers stations. | \r\n
\r\n B. Parity bits\r\n | \r\n
| A parity bit is a bit that is added to a group of source bits to ensure that the number of set bits (i.e., bits with value 1) in the outcome is even or odd. It is a very simple scheme that can be used to detect single or any other odd number (i.e., three, five, etc.) of errors in the output. An even number of flipped bits will make the parity bit appear correct even though the data is erroneous. | \r\n
| Extensions and variations on the parity bit mechanism are horizontal redundancy checks, vertical redundancy checks, and "double," "dual," or "diagonal" parity (used in RAID-DP). | \r\n
\r\n C. Checksums\r\n | \r\n
| A checksum of a message is a modular arithmetic sum of message code words of a fixed word length (e.g., byte values). The sum may be negated by means of a ones''-complement operation prior to transmission to detect errors resulting in all-zero messages. | \r\n
| Checksum schemes include parity bits, check digits, and longitudinal redundancy checks. Some checksum schemes, such as the Luhn algorithm and the Verhoeff algorithm, are specifically designed to detect errors commonly introduced by humans in writing down or remembering identification numbers. | \r\n
\r\n D. Cyclic redundancy checks (CRCs)\r\n | \r\n
| A cyclic redundancy check (CRC) is a singleburst- error-detecting cyclic code and non-secure hash function designed to detect accidental changes to digital data in computer networks. It is characterized by specification of a so-called generator polynomial, which is used as the divisor in a polynomial long division over a finite field, taking the input data as the dividend, and where the remainder becomes the result. | \r\n
| Cyclic codes have favorable properties in that they are well suited for detecting burst errors. CRCs are particularly easy to implement in hardware, and are therefore commonly used in digital networks and storage devices such as hard disk drives.Even parity is a special case of a cyclic redundancy check, where the single-bit CRC is generated by the divisor x+1. | \r\n
\r\n IV.BIT AND BLOCK STREAM CONVERSION\r\n | \r\n
| In this encoder, data bits are provided at a rate of k bits per second. Channel symbols are output at a rate of n = 2k symbols per second. The input bit is stable during the encoder cycle. The encoder cycle starts when an input clock edge occurs. When the input clock edge occurs, the output of the left-hand flip-flop is clocked into the right-hand flip-flop, the previous input bit is clocked into the left-hand flip-flop, and a new input bit becomes available. Then the outputs of the upper and lower modulo-two adders become stable. The output selector (SEL A/B block) cycles through two states-in the first state, it selects and outputs the output of the upper modulo-two adder; in the second state, it selects and outputs the output of the lower modulo-two adder. | \r\n
| The encoder shown above encodes the K = 3, (7, 5) convolutional code. The octal numbers 7 and 5 represent the code generator polynomials, which when read in binary (1112 and 1012) correspond to the shift register connections to the upper and lower modulo-two adders, respectively. This code has been determined to be the "best" code for rate 1/2, K = 3. It is the code I will use for the remaining discussion and examples, for reasons that will become readily apparent when we get into the Viterbi decoder algorithm. | \r\n
| Let''s look at an example input data stream, and the corresponding output data stream: Let the input sequence be 0101110010100012. | \r\n
| Assume that the outputs of both of the flip-flops in the shift register are initially cleared, i.e. their outputs are zeroes. The first clock cycle makes the first input bit, a zero, available to the encoder. The flip-flop outputs are both zeroes. The inputs to the modulo-two adders are all zeroes, so the output of the encoder is 00. | \r\n
 | \r\n
| The second clock cycle makes the second input bit available to the encoder. The left-hand flip-flop clocks in the previous bit, which was a zero, and the right-hand flip-flop clocks in the zero output by the left hand flipflop. The inputs to the top modulo-two adder are 1002, so the output is a one. The inputs to the bottom modulo-two adder are 102, so the output is also a one. So the encoder outputs 112 for the channel symbols. | \r\n
 | \r\n
| The third clock cycle makes the third input bit, a zero, available to the encoder. The left-hand flip-flop clocks in the previous bit, which was a one, and the righthand flip-flop clocks in the zero from two bit times ago. The inputs to the top modulo-two adder are 0102, so the output is a one. The inputs to the bottom modulo-two adder are 002, so the output is zero. So the encoder outputs 102 for the channel symbols. | \r\n
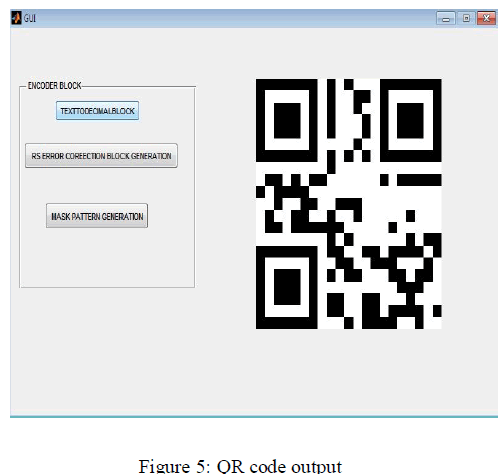
\r\n V. RESULT AND OUTPUT CODE USING MATLAB\r\n | \r\n
| MATLAB (matrix laboratory) is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages, including C, C++, and Fortran. | \r\n
 | \r\n
| Although MATLAB is intended primarily for numerical computing, an optional toolbox uses the MuPAD symbolic engine, allowing access to symbolic computing capabilities. An additional package, Simulink, adds graphical multi-domain simulation and Model-Based Design for dynamic and embedded systems. | \r\n
| Generating the data to be transmitted through the channel can be accomplished quite simply by using a random number generator. One that produces a uniform distribution of numbers on the interval 0 to a maximum value is provided in C: rand (). Using this function, we can say that any value less than half of the maximum value is a zero; any value greater than or equal to half of the maximum value is a one. | \r\n
 | \r\n
| In 2004, MATLAB had around one million users across industry and academia. MATLAB users come from various backgrounds of engineering, science, and economics. MATLAB is widely used in academic and research institutions as well as industrial enterprises. | \r\n
\r\n VI. CONCLUSION AND FUTURE WORK\r\n | \r\n
| The framework proposed here provides an effective method for extending monochrome barcodes to color. The color code constructions offer three times the data rates of their monochrome counterparts, exploiting the spectral diversity provided by color printing and capture systems I conjunction with model-based interference cancellation that mitigates inter-channel coupling introduced by the physical characteristics of the devices. Although, bit error rates and therefore information capacities vary across the three resulting channels, the error rates are in ranges that are readily handled by the error correction coding available for monochrome barcodes. | \r\n
| The interference and the reduction are more pronounced when the dot orientations in the neighboring colorant channels in spectra (cyan-magenta or magentayellow), differ from each other. The bit error rates evaluated for the data embedded in each of the colorant channels in the barcodes, comparing with and without color interference cancellation, where the data is extracted from the estimated print colorant channels. | \r\n
\r\n
References\r\n | \r\n
|
\r\n