Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

A Simple Regression Model for Electrical Energy Forecasting

J. Kumaran @ Kumar1, G. Ravi2
  1. Research Scholar in SCSVMV University, Assistant Professor, Dept of CSE, Pondicherry Engineering College, Puducherry, India
  2. Professor of Electrical and Electronics Engineering, Pondicherry Engineering College, Puducherry, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Long term load forecasting is an important aspect of electric utility resource planning and utility expansion. This paper presents a simple regression analysis based model involving population and per capita GDP for long term forecasting of India’s sector-wise electrical energy demand. The model requires an input, the year of the forecast, and predicts the sector-wise energy demand. Sector-wise energy consumption during the years 1990 -2012 forms the data for developing the forecasting model. It presents the forecasted sector-wise energy demands up to the 2025.

Keywords
load forecasting, regression analysis.
 

INTRODUCTION
Electrical Energy is one of the most important sources for social and economic development of all nations. The growth in energy consumption is essentially linked with the growth in economy. Electricity demand increases due to the population growth, higher per capita consumption, rapid development of industrial & commercial growth, higher Gross Domestic Product (GDP) growth and structural changes in the economy [1,2]. Load forecasting problem has been receiving great and growing attention as being an important and primary tool in power system planning and operation. It has been an attractive research topic in many countries all over the world, especially in fast developing countries like India with higher load growth rate in recent decades. Many techniques such as auto regressive integrated moving average [3] and regression analysis (RA) [4-7] have been investigated to solve the problem of LF in the last few decades. Recently, considerable interest appears to be focused on the application of artificial neural networks for LF due to their ability to extract the relationship among input variables and output through learning from the available database [8-12]. ANNs combined with RA [13-16] as well with fuzzy logic [17,18] for LF have been outlined. Only a few studies have been carried out for medium and long term LF. Hybrid models by combining seasonal exponential adjustment method with the regression methods for predicting one-week-ahead daily load through employing the information of days before being similar to that of the forecast day have been proposed in [19]. A novel hybrid algorithm involving support vector regression with chaotic sequence and genetic algorithm for cyclic LF with a view to improve the forecasting performance and avoid premature convergence has been suggested [20]. A new hybrid shortterm load forecaster using economic indices in order to reduce the impact of economic dynamics such as economic recession on load demand patterns has been developed in [21]. Most of the studies focus on short-term LF.
In this paper, a simple RA based model for long-term forecasting of India’s sector-wise electrical energy demand involving per capita GDP and Population is presented. The paper is organized as follows: section II overviews RM, section III explains the proposed model (PM) along with the results, section IV concludes.

OVERVIEW OF REGRESSION ANALYSIS
Traditional models for LF can be generally classified as time series models and RMs. In time series models, the previous load is extrapolated to obtain future loads. These models are frequently augmented with transfer functions in order to adapt the consumer response to changing weather patterns and intangible factors. These models require large amount of data and a complex estimation procedure. RMs constitute the second major modelling technique, wherein the database is frequently divided into smaller segments, whereby a RM is built for each segment, such as a season or a day or a week.
RA is a technique used for analysing the numerical data. The dependent variable yi is a linear combination of the parameters, α , and the independent variables, xi , which could be linear or nonlinear. The simple linear and multiple linear regressions are the two basic types of linear regression. For instance, in simple regression of N data points’ modelling, there is one independent variable, xi , and two parameters, α 0 and α 1 , which yield a straight line, called fitted regression line:
yi =α 0 +α 1xi +ei i =1,...,N (1)
In multiple linear regressions, there are more than one independent variable or function of independent variables. For example, the preceding regression with 2 xi term gives a parabola:
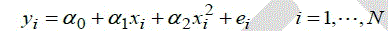image(2)
Although the right-hand side expression is quadratic, it is still considered to be linear regression, as it involves linear parameters, α 0 , α 1 and α 2 .
In the general multiple RMs, there may be m independent variables:
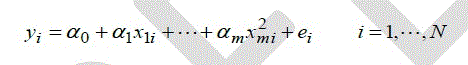image(3)
Where ei is the error term, which represents the unexplained variation in the dependent variable and is treated as a random variable.
In practice, the performance of RM depends on the form of the data-generating process and its relation to the regression approach used. Typically, the best fit is evaluated by using the least squares method, although other criteria are also used.

PROPOSED MODEL
The objective is to develop a simple forecasting model for predicting the sector-wise electrical energy demand, unlike existing models of estimating the net energy demand, for the future years with least input data. The data such as such as weather, average temperature, time, oil price, economy, population, etc., which are related to the electrical energy demand in any country, are usually used in the forecasting models.
Among these factors, the population growth as well the continuous improvement in the public revenue and living standards, represented through per capita GDP, are linked with the total energy consumption of any country [11,13]. Though the per capita GDP and population ascertain a good relationship with the electrical energy demand in the longterm forecasting model, they are not readily available for the future years. However, they can be predicted. The population and per capita GDP are used as inputs in the long term forecasting model suggested in Ref.[11], which fails to develop a tool for obtaining the required input data for the future years, thereby making the model incomplete. The aim is thus to develop a complete model with minimum input for forecasting the sector-wise energy demand unlike the existing models using guessed input values.
The PM comprises two RMs, the former one predicts the population and per capita GDP for a given future year and the later one estimates the sector wise energy demand by considering the output of the former as input. The structure of PM is shown in Fig. 1. A historical data comprising India’s sector-wise energy consumption, the per capita GDP and the population data during the period of 1980-2012, are used to develop the model. [22-24].
The RA is applied to relate the year with per capita GDP and population growth through the procedure described in section–II to build RM-1. Then the per capita GDP and population growth are related with sector wise electrical energy demand through RA to construct RM-2. These two models are combined to form the proposed model. The proposed model receives the year of forecast as the input and predicts initially the population growth and per capita GDP, which are further processed to perform forecasting of sector-wise energy demand.
The intermediate results in terms of per capita GDP and the population, offered by RM-1, for four different yesteryears are presented with the actual values in Table-1. The corresponding predictions of sector wise energy demand, obtained by RM-2, along with their mean absolute percent error (MAPE) are also included in the same table. It is clear from the average MAPE values that the PM offers a forecast, which is nearer to the actual values, thereby ensuring the accuracy of the results for future years. The forecasted sector wise energy demand along with intermediate per capita GDP and population during the years 2013- 2025 are presented in Table-2. It is clear from this table that the net energy demand of 2013 is 814.24 BkWh, while the demand will be 2168.55 BkWh in 2025. The demand in 2025 will increase roughly 2.66 times the demand of 2013. The policy makers of the government as well as the energy utilities should take appropriate steps for construction of new power plants based on the electrical energy requirement by the year 2025.

CONCLUSION
A simple LF model using two RMs, which take into account of the population and per capita GDP, for obtaining sector-wise energy demand, has been suggested. The load demand data involving population and per capita GDP during the years 1980-2012 has been used in developing the PM. The first RM has been designed to predict the population and per capita GDP for a given future year. The second RM has been tailored to forecast the sector-wise energy demand by processing the output of the first network. The PM will help the policy makers for allocating appropriate funds for constructing new generation plants and transmission systems to meet the future demands and attempts to offer reliable service to the customers in the future years.

ACKNOWLEDGEMENT
The authors gratefully acknowledge the authorities of SCSVMV and Pondicherry Engineering College-Puducherry for their continued support, encouragement and the facilities provided to carry out this work.

Tables at a glance
Table icon Table icon
Table 1 Table 2
 

Figures at a glance
Figure
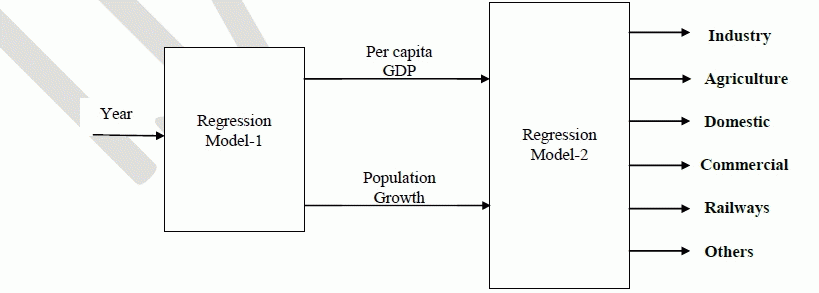Figure 1
 

References