Keywords
|
| Bragg fiber, dispersion, effective area, nonlinearity, photonic crystals. |
INTRODUCTION
|
| The development of optical fibers has played an important role in the information technology (IT) revolution over the past three decades. Optical fiber has been widely applied in backbone networks as well as access networks, to support the continuously growing IT infrastructure. Other significant application areas of optical fibers are medical imaging, beam delivery of medicines, diagnostics, sensing, amplification, laser machining and realization of new classes of optical components and lasers [1]. However, in conventional single – mode optical fibers, the optical characteristics limit the single – mode optical bandwidth at currently used wavelengths. During first two decades, most of the research in optical fibers was directed towards the reduction of losses and the developments were made at incredible rates due to incremental improvement in fabrication process. Since then, a significant part of the research is focused to design new optical fibers with modified structure for tailoring and improvement of optical properties such as losses, nonlinearity, and dispersion and polarization effects. Researchers recognized that a regular morphological structure built – in within the material drastically modifies its optical properties. Such structured materials are known as photonic crystals and the fibers formed using photonic crystals are known as photonic crystal fibers (PCFs) [2]. |
| The idea of photonic crystals was originally given by Sajeev John [3] and Eli Yablonovitch [4] in 1987. They demonstrated that the light guidance can be totally restricted in a periodic arrangement of ideally lossless dielectrics, at certain wavelengths, regardless of the direction of propagation and polarization. This suppression of light is due to periodicity of the arrangement known as photonic band gap (PBG). PBG is the energy or frequency range where the light is totally blocked inside the photonic crystals. When the light with frequency in range of photonic bandgap is incident to the structure, it is completely reflected. However, if a defect is introduced in the periodic structure, the light propagates through the defect due to the photonic bandgap which does not allow the light to enter into the periodic arrangement. Then, the light is guided into the structure as it will be guided in a waveguide. When a band gap is present irrespective of direction of propagation and polarization, it is known as total photonic band gap [5]. Originally, the term photonic crystal was used for the materials with photonic bandgap. Later, it became a common term to refer to any kind of periodic arrangement of dielectrics or metals, with or without photonic band gaps. A photonic crystal with a photonic bandgap is now more commonly known as photonic band gap material. Photonic Crystals can be classified into three categories depending on the geometry of the structure, i.e. one-dimensional (1D), two-dimensional (2D) and three-dimensional (3D) structures [5]. In one dimensional photonic crystal, two alternating dielectric layers are arranged periodically in one direction only, while the structure is uniform in other two directions. Light propagating in perpendicular direction towards the layers experiences successive reflection and transmission at each boundary between adjacent layers. When the layer thickness and refractive indices of the materials are carefully chosen such that, waves reflected from each boundary are in phase and waves transmitted are out of phase. This causes the transmitted wave components to cancel out each other, and only the reflected components add up together and the light is totally reflected. This works only for a range of wavelengths. Bragg mirror is a simplest example of one dimensional photonic crystal [6, 7, 8]. |
| The Bragg fibers are based on 1D photonic crystals, formed by a low-index core surrounded by an alternating cladding of high- and low refractive-index layers. The light is confined to the core by cylindrical Bragg reflection off the alternating layers. In such Bragg fibers, the light guidance is through PBG mechanism. The Bragg fibers can also be formed by high-index core surrounded by an alternating cladding of low- and high refractive-index layers. In such Bragg fibers, the light guidance is through modified total internal reflection mechanism [9, 10]. |
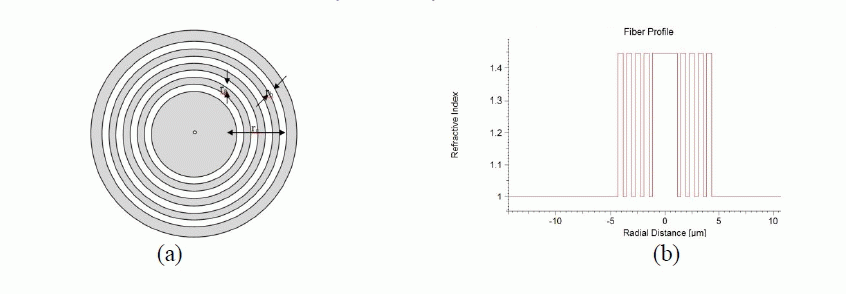
| In this paper, we have designed a High-Index Core Bragg Fiber. It is a cylindrically symmetric microstructured fiber having a high-index core (silica in our case) surrounded by a multilayered cladding made of alternating layers of silica and a lower refractive-index dielectric. Further, we have characterized the fiber using matrix-based modal analysis and calculated various optical properties such as dispersion and effective area. |
RELATED WORK
|
| High-index-core Bragg fiber [11] is a cylindrically symmetric microstructured fiber having a high-index core (usually silica) surrounded by a multilayered cladding made of alternating layers of silica and a lower refractive-index dielectric. In contrast to standard Bragg fibers, guidance is not given in the low-index core, but in the silica core like in central hole missing PCF’s. Because the dispersion produced by the fiber geometry exists in all cases (even guiding light in air), our aim is to compensate for the geometric fiber dispersion by means of the material dispersion corresponding to the material where the mode is propagating. A suitable design of the geometric parameters in Bragg fibers, leads to nearly-zero ultraflattened dispersion [12, 13] or results in new tunable flattened dispersion properties [14]. Likewise, a zero-dispersion wavelength [15] or very large negative dispersion [16] values can be achieved in single-mode cylindrically symmetric layered fibers. using the remarkable dispersion properties due to the Bragg fiber geometry, we can properly compensate the material dispersion of the silica and, then, to achieve a very nice control of the dispersion behavior. |
FIBER DESIGN
|
| We have used silica as core and air-silica layers to design the cladding region of the fiber. Silica fibers have become very popular due to low loss due to refined fabrication processes and low cost due to production at mass scale for telecommunication networks [17]. Due to their large transmission range (0.21 μm – 3.7 μm) and most of the optical instruments and equipments designed around this range, it is always very convenient to work with silica based fibers. Basically, it is very convenient to work with silica fibers because of the following reasons [18]: |
| 1. Highly pure silica can be made very economically due to simple and efficient processes to obtain silica from silicon which is available in abundance. |
| 2. The transmission range of silica is very broad (practically 300 nm to 2500 nm) with its spectral range spanning from visible to near-infrared wavelength. |
| 3. It is very easy to draw silica into an optical fiber due to its physical and chemical properties. The softening temperature of silica is very high (~ 1600°C) with a high transition temperature (~1150°C) and it shows very slow variation in viscosity with change in temperature. These properties make it suitable for drawing fibers. Silica also shows good resistance to humidity and thus deteriorates very slowly with changes in climatic conditions [17]. |
| In contrast to standard Bragg fibers, the light guidance in High-Index Core Bragg Fibers is not given in the low-index core, but in the silica core like in central hole-missing PCFs. Because the dispersion produced by the fiber geometry exists in all cases (even guiding light in air), the aim of our scheme is to compensate for the geometric fiber dispersion by means of the material dispersion corresponding to the material where the mode is propagating (silica in our case). Accordingly, using the remarkable dispersion properties due to the Bragg fiber geometry, we can properly compensate the material dispersion of the silica and, then, to achieve a very nice control of the dispersion behavior. |
| The multilayered structure geometry is characterized by the core radius, rc, low-index layer thickness, ra, and highindex layer thickness, rb. The refractive indices are alternately n2 and n1, where n2<n1. In fact, we have selected the refractive indices of silica and air as n1 and n2, respectively. |
| Radius of the core = 1.15 μm. |
| Width of the air rings = 0.3 μm |
| Width of the solid rings = 0.5 μm |
SIMULATION AND RESULTS
|
Attenuation
|
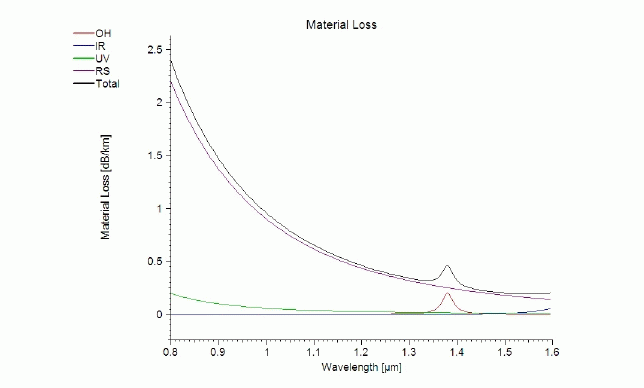
| Attenuation is one of the most important properties of an optical fiber. It plays an important role in long haul communication systems. In fused silica, the minimum loss is ~ 0.2 dB/km at 1550 nm [19, 2]. The intrinsic loss [2] in Bragg fiber denoted by αdB and measured in dB/km, can be expressed as |
| αdB = A/λ4 + B + αOH + αIR |
| where |
| A: Rayleigh scattering coefficient, |
| B: the imperfection loss, |
| αOH: OH absorption losses and |
| αIR: infrared absorption losses. |
| Although, the Rayleigh scattering coefficient of Bragg Fibers is almost same as that of conventional fibers, reducing the roughness of the fiber can lower the Rayleigh scattering coefficient. OH-absorption loss and imperfection loss dominate loss in Bragg Fibers. By improving the etching and polishing process of the fiber can lead to reduction of imperfection loss caused by roughness due to scratches during the fabrication process. OH-absorption loss is due to OH impurities penetrating into the Bragg Fiber core region during the fabrication process. A dehydration process can be used to reduce the OH-absorption loss [2]. |
| Fused silica has attenuation ~0.2 dB/km in spectral range of 1300 – 1600 nm. This attenuation increases with shifting of the wavelength on both shorter and longer wavelength sides. On shorter wavelength side, it increases due to Rayleigh scattering whereas on longer wavelength side, it increases due to phonon absorption. |
Dispersion
|
| The chromatic dispersion D of a Bragg Fiber [20] can be calculated from the effective index of the fundamental mode, neff for a wavelength range using |
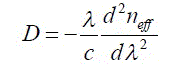 (1) (1) |
| where c is the velocity of light in a vacuum. |
| Chromatic Dispersion D, is also expressed as sum of material dispersion Dm and waveguide dispersion, Dw. |
| D=Dm+Dw (2) |
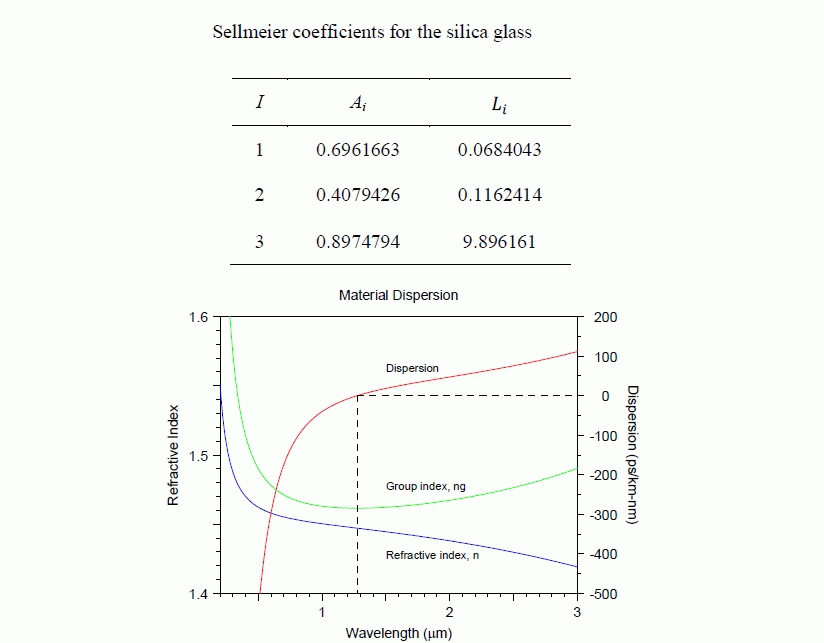
| Material dispersion of silica can be derived from the spectral refractive index of silica. The refractive index of bulk silica [21, 22] can be represented by Sellmeier equation given by Eq. 3 and the taμble gives the values of fitting coefficients Ai and Li. |
 (3) (3) |
| Figure 3 shows the dispersion characteristics of silica calculated from Eq. 3 and Table. The wavelength at which the GVD is zero is called zero dispersion wavelength (~1288 nm for silica). At around this wavelength, the group index also changes the way it is varying with wavelength. At shorter wavelengths, the group index decreases with increase in wavelength but for wavelengths longer than ZDW, the group index increases with increase in wavelength. When the dispersion D, is below zero, the dispersion is said to be normal and when the dispersion D is above zero, the dispersion is called anomalous dispersion. |
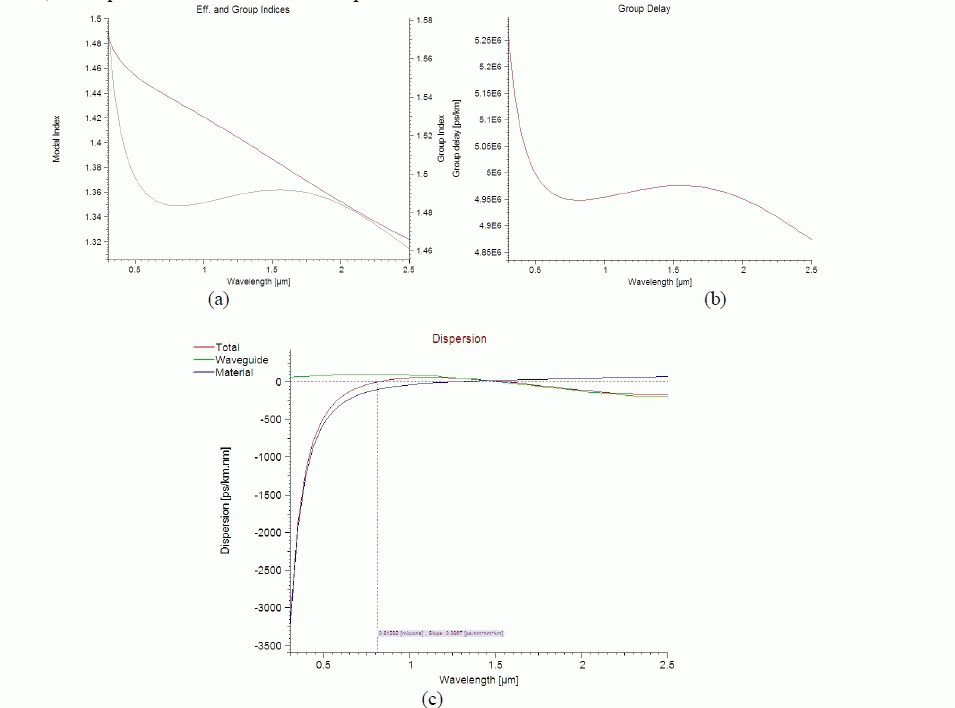
| We have extensively studied the dispersion properties of different High-Index Core Bragg Fiber designs. We expect to tailor the chromatic dispersion of such fibers by manipulating the geometry of the multilayered cladding. The total dispersion, D, can be given, as a first approximation, in terms of the material dispersion, Dm, and the geometric waveguide dispersion, Dg, using the approximate expression D = Dm + Dw. The evaluation of Dw is carried out by considering that the material refractive indices are wavelength independent. Therefore, its dependence on the wavelength arises from the fiber geometry exclusively. The interplay between the fixed silica dispersion and the tunable waveguide dispersion allows us to control the dispersion properties of this new structure. For this reason we have systematically studied the dependence of Dw in terms of the geometric parameters, rc, ra, and rb. For this we have followed a design procedure which is based on the above approximate expression for D, one can obtain approximate values for rc, ra, and rb providing a desired constant dispersion profile. And, then, starting from the approximate values for rc, ra, and rb, we can fine tune these parameters to obtain the expected dispersion behavior. Using this procedure, we have studied the dispersion properties of different silica-air fiber designs with ZDW around 850 nm and 1.55 μm. We would like to emphasize that all results refer to the fundamental mode. |
| Fig. 4 shows the refractive and group indices, group delay, and material, waveguide and total dispersion of High-Index Core Bragg Fiber. Due to continuous and fast decrease in modal index of fiber below 700 nm as show in Fig 4 (a), the dispersion of fiber increases rapidly and the group index decreases rapidly. At zero dispersion wavelengths, the group index and group delay change the way they are varying with wavelength (Fig. 4 (a) and 4 (b)). The fiber is designed to have Zero Dispersion Wavelengths (ZDWs) around 0.8 μm and 1.55 μm as shown in Fig 4 (c). This unique position of ZDWs of the fiber makes it suitable for both telecom and nontelecom applications. Also, economic and compact optical sources are available at these wavelengths which make the overall systems using this fiber very cheap. This Highindex- core Bragg fibers is designed to achieve an ultraflattened dispersion behavior in anomalous region. It is worth noting that this ultraflattened behavior is preserved in a large wavelength window that extends over several hundreds of nanometers. |
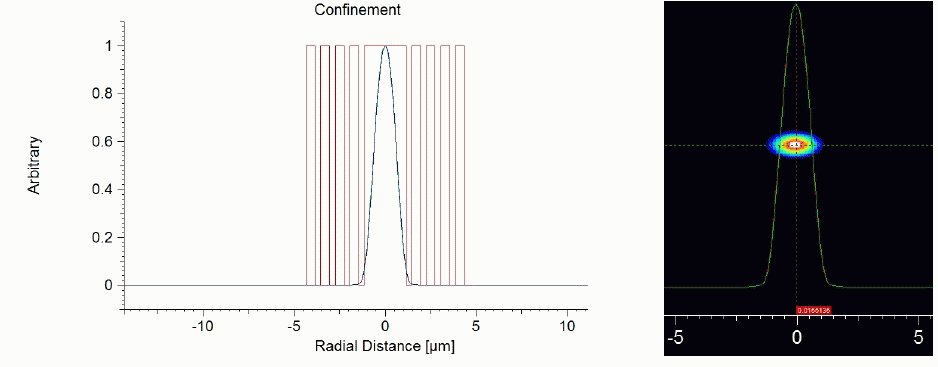
| Fig. 5 shows the modal field confinement of the fiber and as it can be clearly seen that the fiber is single mode as most of the electric field is concentrated in the core region and only one peak exists in the electric field profile. Due to this single-mode property of the fiber, it is a potential candidate for telecommunication applications in visible as well as near IR applications. |
Effective Area
|
| Effective area of the core plays a very important role in determining the nonlinear properties of an optical fiber. A low effective area is useful in achieving the desired nonlinear effects at low input power. The effective area can also be related to the spot – size w, 2 Aeff =π w2 . |
| The effective area of the fiber core Aeff, is defined as, |
 (8) (8) |
| where Et is the transverse electric field vector and S denotes the fiber cross section [19]. With increase in air-hole diameter, the mode becomes tightly confined; this leads to reduction in both effective area and confinement loss. However, the effective area is very less sensitive to increase or decrease in number of air-hole rings whereas confinement loss reduces significantly with increase in number of air-hole rings. |
| In Bragg Fibers, a very high index contrast can be achieved by reducing the core size. This pushes the light into the silica core and the guided mode is strongly confined. Due to high field intensity in the core, nonlinear properties of the fiber are enhanced. The non-linearity coefficient γ is given by |
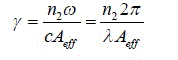 (9) (9) |
| where 2 n is nonlinear refractive index of the material. Effective area Aeff plays an important role in nonlinear phenomena in PCFs. |
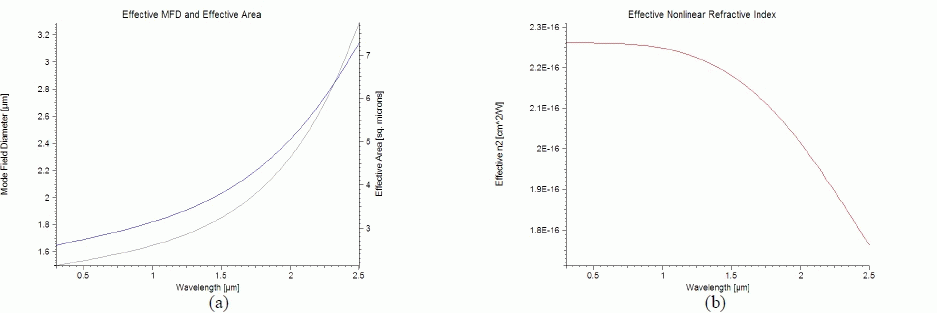
| Bragg fibers offer the possibility of much tighter mode confinement than conventional optical fibers due to high index difference between silica core and air-silica cladding and thus smaller effective area. Fig. 6 (a) shows the variation in effective area of the fiber with wavelength. The effective MFD and thus the effective area of the fiber increases rapidly with increase in wavelength and at the same time effective nonlinear refractive index of silica also decrease (Fig 6 (b)). Therefore, at the wavelengths above 1.6 μm, nonlinearity decreases rapidly with the increase in wavelength. But in the below 1.6 μm, the nonlinear refractive index as well as effective area are contributing towards high nonlinearity of the fiber making it a potential candidate for nonlinear applications such as supercontinuum generation and optical parametric amplification. Location of ZDW below 1.6 μm adds on to the suitability of fiber for 0.8 μm and 1.55 μm applications. |
CONCLUSION
|
| In this report, we have designed and discussed the dispersion properties, effective area of High-Index Core Bragg fibers with ultraflattened dispersion in anomalous region and dispersion-compensating characteristics in normal region. The designed fiber has ZDWs around 0.8 μm and 1.55 μm. All these characteristics make the fiber suitable for a variety of telecom and nontelecom applications in visible region. |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
 |
 |
 |
| Figure 4 |
Figure 5 |
Figure 6 |
|
| |
References
|
- A. W. Snyder and J. D. Love, Optical Waveguide Theory. London: Chapman & Hall, 1983.
- F. Poli, A. Cucinotta, and S. Selleri, Photonic Crystal Fibers: Properties and Applications. Springer, 2007.
- S. John, "Strong localization of photons in certain disordered dielectric superlattices," Physical Review Letters, vol. 58, pp. 2486-2489, 1987.
- E. Yablonovitch, "Inhibited spontaneous emission in solid state physics and electronics," Physical Review Letters, vol. 58, no. 20, pp. 2059– 2062, 1987.
- J. D. Joannopoulos, S. G. Johnson, J. N. Winn, and R. D. Meade, Photonic Crystals: Molding the Flow of Light, 2nd ed.: Princeton University Press, 2008.
- F. Zolla, et al., Foundations Of Photonic Crystal Fibres. World Scientific, 2005.
- I. A. Sukhoivanov and I. V. Guryev, Photonic Crystals: Physics and Practical Modeling.: Springer, 2009.
- A. K. Abeeluck, N. M. Litchinitser, C. Headley, and B. J. Eggleton, "Analysis of spectral characteristics of photonic bandgap waveguides," Optics Express, vol. 10, no. 23, pp. 1320-1333, November 2002.
- P. Yeh, A. Yariv, and E. Marom, "Theory of Bragg fiber," Journal of Optical Society of America, vol. 68, no. 9, pp. 1196-1201, Sep. 1978.
- N. J. Doran and K. J. Blow, "Cylindrical Bragg Fibers: A Design and Feasibility Study For Optical Communications," Journal of Lightwave Technology, vol. 1, no. 4, pp. 588-590, Dec. 1983.
- J. A. Monsoriu, E. Silvestre, A. Ferrando, P. Andrés, and J. J. Miret, "High-index-core Bragg fibers: dispersion properties," Optics Express, vol. 11, no. 12, pp. 1400-1405, Jun. 2003.
- A. Ferrando, E. Silvestre, J. J. Miret, and P. Andr´es, "Nearly zero ultraflattened dispersion in photonic crystal fibers," Optics Letters, vol. 25, p. 790–792, Jun. 2000.
- W. H. Reeves, J. C. Knight, P. S. J. Russell, and P. J. Roberts, "Demonstration of ultra-flattened dispersion in photonic crystal fibers," Optics Express, vol. 10, p. 609–613, Jul. 2002.
- A. Ferrando, E. Silvestre, P. Andres, J. Miret, and M. Andres, "Designing the properties of dispersion-flattened photonic crystal fibers," Optics Express, vol. 9, no. 13, pp. 687-697, Dec. 2001.
- G. Ouyang, Y. Xu, and A. Yariv, "Comparative study of air-core and coaxial Bragg fibers: singlemode transmission and dispersion characteristics," Optics Express, vol. 9, pp. 733-747, 2001.
- G. Ouyang, Y. Xu, and A. Yariv, "Theoretical study on dispersion compensation in air-core Bragg fibers," Optics Express, vol. 10, pp. 899- 908, 2002.
- M. J. Weber, Handbook of Optical Materials.: CRC Press, 2003.
- J.M. Dudley and J.R. Taylor, Supercontinuum Generation in Optical Fibers.: Cambridge University Press, 2010.
- G.P. Agrawal, Nonlinear fiber optics, 4th ed.: Academic Press, 2007.
- B. Kuhlmey, G. Renversez, and D. Maystre, "Chromatic dispersion and losses of microstructured optical fibers," Applied Optics, vol. 42, no. 4,
- R. Kitamura, L. Pilon, and M. Jonasz, "Optical constants of silica glass from extreme ultraviolet to far infrared at near room temperature," Applied Optics, vol. 46, no. 33, pp. 8118-8133, November 2007.
- I. H. Malitson, "In erspecimen Comparison of the Refractive Index of Fused Silica," Journal of the Optical Society of America, vol. 55, no. 10, pp. 1205-1208, October 1965.
|