A Two Stage Batch Arrival Queue with
Compulsory Server Vacation and Second
Optional Repair

N. Balamani

A Two Stage Batch Arrival Queue with Compulsory Server Vacation and Second Optional Repair

N. Balamani

Assistant Professor, Department of Mathematics, Avinashilingam Institute for Home Science and Higher Education for Women University, Coimbatore, Tamil Nadu, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

This paper deals with a single server batch arrival queue, two stages of heterogeneous service with different (arbitrary) service time distribution subject to random breakdowns followed by a repair and compulsory server vacations with general (arbitrary) vacation periods. After first stage service the server must provide second stage service. However after the completion of each second stage service the server will take compulsory vacation. The system may breakdown at random and it must be send to repair process immediately. If the server could not be repaired with first essential repair, subsequent repairs are needed for the restoration of the server. Both first essential repair and second optional repair times follow exponential distribution The steady state solutions have been found by using supplementary variable technique. Also the mean queue length and the mean waiting time are computed.

Keywords

Batch Arrivals, Breakdowns, Steady state, First essential repair, Second optional repair, Mean queue length, Mean waiting time

I.INTRODUCTION

Vacation queues have been studied by numerous authors including Levy and Yechiali [8] Doshi [4,5] and Keilson and Servi[ 7] due to their wide applications in manufacturing and telecommunication systems. Vacation queues with c servers have been studied by Tian et al. [ 11]. Choudhury and Borthakur [3] have studied vacation queues with batch arrivals. Baba [2] employed the supplementary variable technique for deriving the transform solutions of waiting time for batch arrival with vacations. Multiple vacations have been studied by Tian and Zhang [12]

In real life situations, a queueing system might suddenly breakdown and hence the server will not be able to provide service unless the system is repaired. Madan and Maraghi[ 9] have studied batch arrival queueing system with random breakdowns and Bernoulli schedule server vacation having general vacation time. They have obtained steady state results in terms of the probability generating functions for the number of customers in the queue. Thangaraj and Vanitha [10] analysed a queueing system with compulsory server vacation and random breakdown.

The most realistic aspect in modelling of an unreliable server is multi optional repair. When server could not be repaired or restored by the first essential repair, subsequent repairs are needed to restore the server. Queues with multi optional repairs were considered by many others. Hsieh et al.[6] studied a queueing model in which the server is subject to several types of breakdowns and each type has two possible stages of repair. William Gray et al.[13]studied a queueing model with multiple types of server breakdown requires a finite random number of stages of repair. Ayyappan and shyamala[1] investigated batch arrival queue with second optional repair.

In this paper we consider a batch arrival queue where each arriving customer has to undergo two stages of service provided by a single server, one by one in succession. As soon as the second stage of a customer’s service is complete, the server will go for compulsory vacation. The system may breakdown at random with breakdown rate  >0. As soon as the system is break down, it is immediately sent for repair wherein the repairman or repairing apparatus provides the first essential repair (FER). After the completion of (FER), the server may opt for second optional repair (SOR) with probability p or may join the system with complementary probability 1-p to render the service to the customers. Both first essential repair and second optional repair times follow exponential distribution. After the completion of the required repair, the server resumes its work immediately. And once the system breakdown, it enters repair process and the customer whose service interrupted goes back to the head of the queue.

II.MATHEMATICAL MODEL

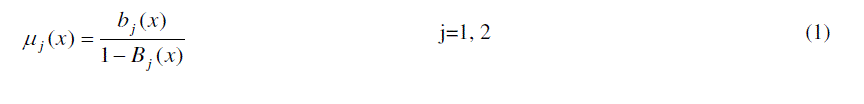6.On returning from vacation the server instantly starts serving the customer at the head of the queue if any. 7.The system may breakdown at random and breakdowns occur according to Poisson stream with mean breakdown rate  >0. The customer receiving service during breakdown returns back to the head of the queue. 8.Once the system breaks down, it is immediately sent for repair wherein the repairman or repairing apparatus provides the first essential repair (FER). After the completion of (FER), the server may opt for second optional repair (SOR) with probability r or may join the system with complementary probability 1-r to render the service to the customers. 9.The repair process provides two types of repair in which the first type of repair is essential and the second type of repair is optional. Both exponentially distributed with mean 1 1  and 2 1  .After the completion of the required repair, the server provides service with the same efficiency as before failure according to FCFS discipline. 10. Various stochastic processes involved in the system are assumed to be independent of each other.

III. DEFINITIONS AND NOTATIONS

We define

P x t j n Probability that at time t , server is active providing jth stage ( j 1,2) service and there are n( 0) customers in the queue excluding the one customer in jth stage (j=1,2) being served and the elapsed service time for

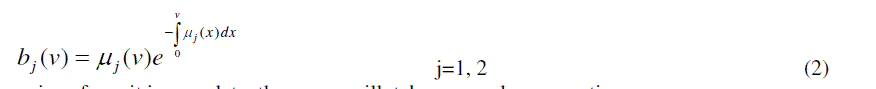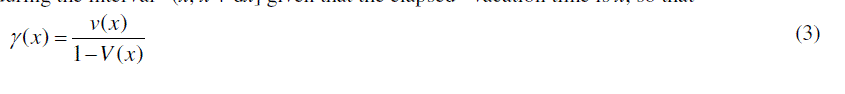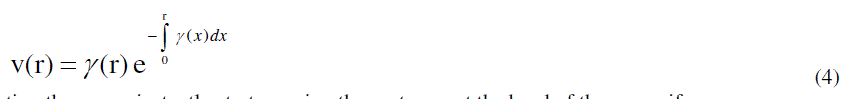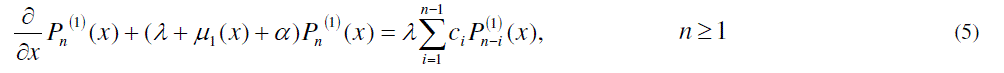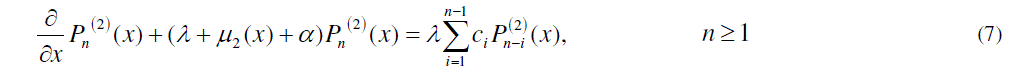References

G.Ayyappan and S.Shyamala, M[X]/G/1 with Bernoulli schedule server vacation random breakdown and second optional repair, Journal of Computations and Modelling, Vol.3, No.3 (2013), 159-175.
Y. Baba, On the M[X]/G/1 queue system with vacation times,Operation Research Lett.,, 5, (1986), 93-98.
A. Borthakur and G. Choudhury, On a batch arrival Poisson queue with generalised vacation, Sankhya Ser.B, 59 (1997), 369-383.
B. T. Doshi, A note on stochastic decomposition in a GI/G/1 queue with vacations or setup times, Journal of Applied Probability, 22( 1985), 419-428.
B. T. Doshi, Queueing systems with vacations - A survey, Queueing Systems,1(1986), 29-66.
Hsieh, Yi-Chih and M. S Andersl, “single server systems with multiple breakdown models,Microelectronics Reliability, 35(1995), 309-318.
J. Keilson and L.D..Servi, Dynamics of the M/G/1 vacation model, Operations Research, Vol.35(1987), 575-582.
Y.Levy and U. Yechiali, Utilization of idle time in an M/G/1 queueing system, Management Science, 22(1975), 202-211.
F.A. Maraghi, K.C. Madan and K.D. Dowman, Batch arrival queueing system with random breakdowns and Bernoulli schedule server vacations having general time distribution, International Journal of Information and Management Sciences, 20 (2009), 55-70
V.Thangaraj and S.Vanitha, M/G/1 Queue with two stage heterogeneous service compulsory server vacation and random breakdowns, International Journal of Contemporary Mathematical Sciences, Vol.5,No.7(2010),307-322
N. Tian, Q. Li and J. Cao, Conditional stochastic decomposition inM/M/c queue with server vacations, Stochastic Models, 15 (1999), 367-377.
N. Tian and Z.G. Zhang, The discrete-time GI/Geo/1 queue with multiple vacations, Queueing Systems, 40 (2002), 283-294.
J. William Gray, P. Patrick Wang and Meckinley Scott, A Queueing model with multiple types of a server breakdowns, Quality technology and Quantitative Management, 1(2)(2004), 245-255.