Keywords
|
| Image Compression, Vector Quantization, Residual Codebook, Modified Fuzzy Possibilistic C-Means, Repulsion, Weighted Mahalanobis Distance. |
INTRODUCTION
|
| Digital Images comes the serious issue of storing and transferring the huge amount of data representing the images. Because the uncompressed multimedia data requires considerable storage capacity and transmission bandwidth. Image Compression is a mapping from a higher dimensional space to a lower dimensional space. Image Compression plays an important role in many multimedia applications. |
| Image compression can be classified into Lossy Compression and Lossless Compression. In Lossless Compression, the original image can be completely recovered from the compressed image. Lossless Compression is applied for applications with rigorous needs such as medical imaging. Whereas Lossy Compression is particularly appropriate for natural images like photos in applications where minor loss is acceptable to accomplish a considerable decrease in bit rate. This paper focuses on Lossy Compression technique using Vector Quantization for compressing an image. |
| Vector Quantization (VQ) is a block-coding technique that quantizes blocks of data instead of single sample. VQ exploits the correlation between neighboring signal samples by quantizing them together. VQ Compression contains two components: VQ encoder and decoder as shown in Fig.1. |
| At the encoder, the input image is partioned into a set of non-overlapping image blocks. The closest code word in the code book is then found for each image block. Here, the closest code word for a given block is the one in the code book that has the minimum squared Euclidean distance from the input block. Next, the corresponding index for each searched closest code word is transmitted to the decoder. Compression is achieved because the indices of the closest code words in the code book are sent to the decoder instead of the image blocks themselves |
| In this paper, an efficient low bit rate image compression scheme is proposed based on VQ that makes use of compression of indices of VQ and residual codebook with Modified Fuzzy Possibilistic C-Means with repulsion. To generate codebook, Modified Fuzzy Possibilistic C-Means technique is used and to improve the accuracy of clustering repulsion term is used. The distance measure used in the conventional technique is modified using Weighted Mahalanobis Distance. |
| The rest of the paper is organized as follows: In section II, the literature survey is presented. The proposed technique is described in section III. Performance of the proposed system is evaluated in section IV and section V concludes the paper. |
LITERATURE SURVEY
|
| Mei Tian [1] proposed a new approach to image compression based on fuzzy clustering. This algorithm operates in four steps |
| Step 1 : Prefiltering, Image Enhancement on fuzzy logic, smoothing and creation of crisp image. |
| Step 2 : Transform each sub block by using DCT |
| Step 3 : Selection of peak values of membership functions by Zigzag method. |
| Step 4 : Compression by run length coding. |
| This method does not include mathematically iteration and hence it takes little time to reach the result. It provides better compression ratio when compared to FCM and HCM. |
| Xiao-Hong eta al.,[2] presented a novel approach on Possibilistic Fuzzy C-Means Clustering Model using Kernal Methods. KPFCM model is dependent on Non-Euclidean distance. In this Kernal Approaches, the input data can be mapped into a high-dimensional attribute space where the nonlinear pattern looks linear. KPFCM can deal noises or outliers superior than PFCM. The experimental result shows that KPFCM provides significant performance |
| Yang et al., [3] puts forth an unlabeled data clustering method using a Possibilistic Fuzzy C-Means (PFCM). It is the integration of Possibilistic C-Means (PCM) and Fuzzy C-Means (FCM). It is used for solving the noise sensitivity issue in FCM and helps to avoid coincident clusters problem in PCM. The goal of PFCM function is customized, with the intention that cosine similarity measure is integrated in this method. The study demonstrated HPFCM is capable of managing complex high dimensional data sets and attain more stable performance. |
| Sreenivasrao et at., [4] presented a Comparative Analysis of Fuzzy C-Means (FCM) and Modified Fuzzy Possibilistic C-Means (MFPCM) Algorithms in Data Mining. The Performance of Fuzzy C-Mean (FCM) clustering algorithm is analyzed. Difficulty of FCM and MFPCM are measured for different data sets. The FCM uses fuzzy partitioning such that a point can fit in to all groups with different membership grades between 0 and 1. This approach helps for managing the difficulties related to understandability of patterns, noisy data, mixed media information and human interaction and can offer estimated solutions quicker. |
| R.Nagendran et al., [5] presented a novel vector quantizer code book design using Fuzzy Possibilistic C-Means clustering technique for image compression using wavelet packet. In this approach, the original image was decomposed into two level wavelet packet tree decomposition and the significant coefficients were taken for the quantization. In quantization process, initially, a code book of size 256 is randomly initialized. It is then trained with important coefficients using FPCM approach. Ultimately, this is encoded using Huffman Encoder. The experimental result shows that FPCM gives better PSNR values than LBG, K-Means, FCM and PCM. |
METHODOLOGY
|
| This scheme has two components Compression of indices and generation of residual codebook. These two components are described in the following section. |
| A. Compression of Indices |
| In the conventional basic memory less VQ, the image blocks are processed independently. However since the size of the blocks used in VQ is very small, typically 4x4, there exists high correlation between image blocks. The bit rate can be further reduced if the interblock correlation is approximately exploited. Several techniques which exploit the interblock correlation have been presented. However these techniques reduce the bit rate at the cost of either quality degradation or large amount of computation / complexity. Search-order coding (SOC) is an efficient technique for further coding the output indexes of the memory less VQ system. It does not introduce extra distortion & requires small computation. Also it alleviates the problems. As stated above, when the image blocks are vector quantized many neighbouring blocks correspond to the same index, since high correlation exists among blocks. The characteristic of high index correlation allows us to further reduce the bit rate [9]. |
| In this work, we adopt a simple searching scheme to find out the matched index from the previous indexes. The corresponding search order of the matched previous index is then sent to the decoder. |
| The search order (SO) is defined as the order that a previous index is compared with the current index. In order to find out the matched index efficiently, we search the previous indexes in a predefined manner. |
| An interesting problem is how many previous indexes should be compared with the current index. Here, we define the search range SR to represent the maximum number of previous indexes to be compared with the current index. It is clear that if we adopt larger SR the possibility for finding out the matched index is higher. However, it needs more bits to code the corresponding index. Index of the codeword of a block is encoded through the degree of the similarity of the block with earlier encoded upper left blocks. When, the degree of similarity of the present block with one of the two earlier encoded blocks is high, the index of the codeword of the block is encoded using the index of the neighbouring codeword. If the degree of similarity of the block with the neighbouring blocks is not high, it is understood that the closest match codeword of the present block may be nearer to the codewords of the neighbouring blocks. |
| B. Construction of Residual Codebook (RC) |
| Residual codebook is constructed using absolute error values caused by VQ method. In the residual codebook construction, the image blocks that are less similar to their closest match code words found in the codebook are taken into account. Less similarity blocks will increase distortion than high similarity blocks in the reconstructed image. Residual codeword (RYi) for a less similarity image block is constructed by comparing it with its closest match codeword. The collection of residual codewords RYi, RYi+1… is called residual codebook. Similarity of an image block x with its closest match codeword Yi is determined based on minimum distortion rule (α) between them. If the mean square error (α) of an image block is greater than a predefined threshold value (σ), then the block is taken as less similarity block. |
| Let x = (x0,x1,…,xk-1) be a k-pixels image block and Yt = (y0,y1,…,yk) be a k-pixels closest match codeword, then the α is defined as : |
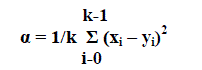 (1) (1) |
| The steps used for constructing residual codebook are given below: |
| Step 1 : An image which is to be compressed is decomposed into a set of non-overlapped image blocks of 4x4 pixels. |
| Step 2 : A codebook is generated for the image blocks using LBG algorithm. |
| Step 3 : Pick up the next codeword Yi form the codebook C and find its all closest match less similarity image blocks (X) found out α from the given set of image blocks and construct residual codeword RYi using the following equation. |
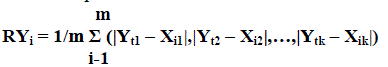 (2) (2) |
| Where k represents the number of elements in the codeword Yi and the image block Xi respectively and m denotes the number of less similarity image blocks that are closer to the codeword Yt. |
| Step 4 : Repeat step 3 until no more codeword exists in the codebook. |
| C. Fuzzy Possibilistic Clustering Algorithm |
| The fuzzified form of the k-means algorithm is Fuzzy C Means (FCM). It is a clustering approach which permits one piece of data to correspond to two or more clusters and extensively used in pattern recognition. This approach is an iterative clustering technique that provides an optimal c partition by reducing the weighted inside group sum of squared error objective function JFCM: |
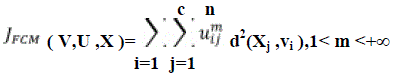 (3) (3) |
| In the equation X = {x1, x2,...,xn} ⊆Rp is the data set in the p-dimensional vector space, the number of data items is symbolized as p, c which denotes the number of clusters with 2 ≤ c ≤ n-1. V = {v1, v2, . . . ,vc} is the c centers of the clusters, vi denotes the p-dimension center of the cluster i, and d2(xj, vi) denotes the space between object xj and cluster centre vi. U = {μij} symbolizes a fuzzy partition matrix with uij = ui (xj) is the degree of membership of xj in the ith cluster; xj is the jth of p-dimensional calculated data. The fuzzy partition matrix satisfies: |
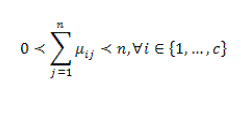 (4) (4) |
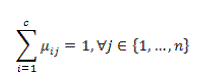 (5) (5) |
| m is a weighting exponent constraint on every fuzzy relationship which produces the level of fuzziness of the resultant classification; it is a predetermined number larger than one. Under the constraint of U the objective function JFCM can be reduced. In particularly, taking the value of JFCM in accordance with uij and vi and zeroing them respectively, is essential but not adequate conditions for JFCM to be at its local extrema will be as the following : |
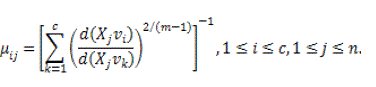 (6) (6) |
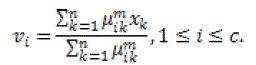 (7) (7) |
| In noisy atmosphere, the memberships of FCM constantly do not fit well to the degree of belonging of the data, and possibly will be inexact. This is primarily because the real data inevitably contains some noises. In order to avoid this limitation of FCM, the constrained condition (3) of the fuzzy c-partition is not considered to accomplish a possibilistic type of membership function and suggested PCM for unsupervised clustering. The component created by the PCM corresponds to a crowded area in the data set; each cluster is independent of the other clusters in the PCM approach. |
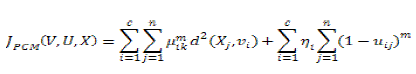 (8) (8) |
| Where |
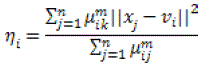 (9) (9) |
| ηiis the scale parameter at the ith cluster, |
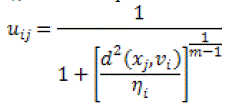 (10) (10) |
| The possibilistic distinct value of training model xj is symbolized as u of the cluster i. m ∈ [1,∞] is a weighting aspect and it is considered to be the possibilistic constraint. PCM is also depending on initialization distinctive of other cluster techniques. In most cases, the clusters will not contain more mobility in PCM approaches, since all data point is categorized as only one cluster at a time without processing all the clusters concurrently. Consequently, a suitable initialization is necessary for the algorithms to converge to almost global minimum. |
| The features of both fuzzy and possibilistic c-means techniques is integrated. Memberships and typicalities are very important parameters for the accurate characteristic of data substructure in clustering complexity. As a result, an objective function in the FPCM depending on the memberships and typicalities is characterized as below: |
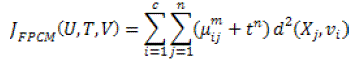 (11) (11) |
| with the following constraints : |
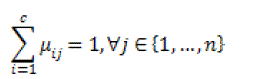 (12) (12) |
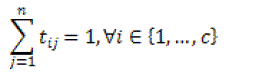 (13) (13) |
| The result of the objective function can be attained by a iterative approach where the degrees of membership, typicality and the cluster centers are modified with the equations given below. |
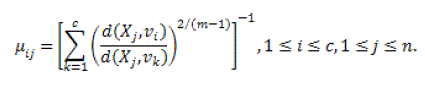 (14) (14) |
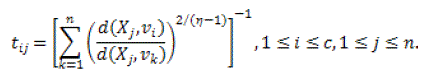 (15) (15) |
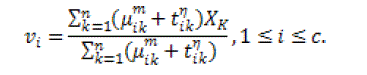 (16) (16) |
| FPCM assembles memberships and possibilities concurrently, along with the common point prototypes or cluster centers for all clusters. Hybridization of possibilistic C-means (PCM) and fuzzy C-means (FCM) is the FPCM that frequently ignores many difficulties of PCM, FCM and FPCM. The noise sensitivity flaw of FCM is eliminated by PFCM, which avoids the concurrent clusters difficulty of PCM. But the evaluation of centroids is controlled by the noise data. Hence a new parameter weight is added to every vector which gives a better classification especially in the care of noise data. The following equation is used to compute the weight |
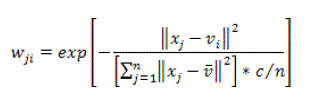 (17) (17) |
| As a result, the objective function of MFPCM is given as follows |
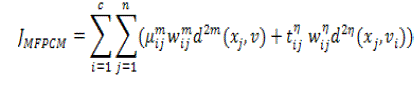 (18) (18) |
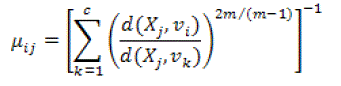 (19) (19) |
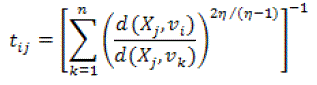 (20) (20) |
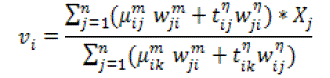 (21) (21) |
| The main disadvantage of the MFPCM is the fact that the objective function is truly reduced only if all the centroids are identical. The typicality of a cluster is based only on the space between the points to that cluster. To overcome this disadvantage and to improve the estimation of centroids, typicality and to lessen the undesirable effect of outliers, this algorithm is combined with repulsion. |
| As a result the objective function is |
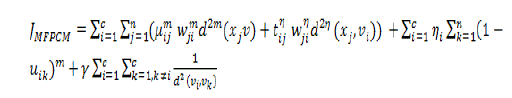 (22) (22) |
| The weighting factor γ is generated to stabilize the attraction and repulsion force that is reducing the intradistances within the clusters and increasing the interdistances among the clusters. |
| D. Feature Weighted Mahalanobis Distance |
| The Mahalanobis distance is one of the basic and widely used approaches as a distance measure for classification. Hence, the Mahalanobis distance should be used as an origin of this new weighted distance metric. The features which are indistinct by noise, have a higher influence on the distance measure than the less indistinct features as they are further away from the feature mean of the class. Thus, the influence of these features should be lowered by reducing their weight. In order to identify the features which have the strongest influence on the distance, the Mahalanobis distance equation is solved for every single feature c over all input samples I and classes j and store the value in Z : |
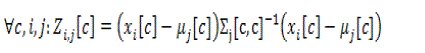 (23) (23) |
| The main aim is to give less weight to the features with high distance and vice versa to avoid the masking of the features with small distances. |
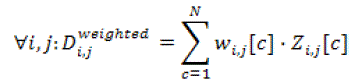 (24) (24) |
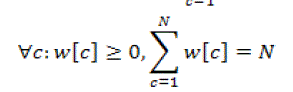 (25) (25) |
| Thus, proper weights have to be chosen. A lot of various reasonable ways exist, e.g. giving zero weight to the feature with the highest distance and normalize the other weights. |
| E.Descent Feature Weights |
| In this approach, the main aim is to select the weights such that all features have the similar influence on the distance measure. Hence, these features under consideration of their average distance have to be normalized. Initially, the vectors of the Mahalanobis distance have to be sorted over their values in the ascending order |
| Then, all samples and classes have to be summed up and normalized by the number of samples and classes |
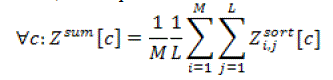 (26) (26) |
| If not all samples to classify are known beforehand, the summation of all samples can be replaced with the sample to classify with nearly no loss in accuracy (on our test set it was below 0.1%). |
| In order to derive the weights under the two constraints (25) the distances have to be first inverted and then normalized. |
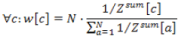 |
| With the given weights the descent feature weighted distance can now easily be obtained by (24). |
| The descent or difference feature weighted distance can now simply be implemented into the MFPCM by replacing the Mahalanobis distance by the novel distance measures |
| F. Proposed Algorithm |
| The proposed scheme combines compression of VQ indices and Modified Fuzzy Possibilistic C-Means with Repulsion and weighted Mahalanobis distance. In this algorithm, VQ based compression technique is established using Modified Fuzzy Possibilistic C-Means with Weighted Mahalanobis distance for better determining the distance between the clusters. The steps used in this compressor are as follows: |
| Step 1 : An image which is to be compressed is decomposed into a set of non-overlapped image blocks of size 4x4 pixels. |
| Step 2 : A codebook is generated for the image blocks using Modified Fuzzy Possibilistic C-Means with Repulsion and weighted Mahalanobis distance. |
| Step 3 : Construct a Residual Codebook for those image blocks (less similarity blocks) whose α is greater than σ. |
| Step 4 : Pick the next image block (current block) and find its closest match codeword in the codebook. Calculate mean square error α for the image block using equation (1) and index of the codeword is encoded using VQ indices compression scheme |
| Step 5 : if (α ≤σ), the current block is encoded as “0” Else the current block is encoded as “1” followed by interpolated residual sign bit plane is computed |
| Step 6 : Repeat step 4 until no more blocks exist in the image. |
| The compressed images decoded by reversing all the previously explained steps and residual block is reconstructed and added for all less resemblance block. |
EXPERIMENTS AND RESULTS
|
| This section clearly illustrates the performance evaluation of the proposed MFPCM with Weighted Mahalanobis distance and repulsion with the existing approaches like FPCM and MFPCM. |
| A. Coding of VQ Indices |
| The performance of the proposed scheme which uses MFPCM with Weighted Mahalanobis distance and repulsion clustering approach for code book generation is evaluated with the existing techniques for different gray- scale images of size 512x512 and is given in Table 4.1. |
| The bits / index value obtained by the proposed MFPCM with Weighted Mahalanobis and repulsion is 2.42 for the Lena image where as it is high for the existing approaches like FPCM and MFPCM. |
| It can be clearly observed from Figure 4.1 that the proposed method MFPCM with Weighted Mahalanobis distance and repulsion has an improvement in coding of VQ indices when compared to the other existing clustering techniques. The proposed approach takes very less bits/index values for the standard images like Lena, Cameraman and Peppers. |
| B. PSNR Values |
| The comparison of PSNR values for the Lena, Cameraman and Pepper images of 512x512 bits when compressed to combine VQ method and Codebook using FPCM, MFPCM and MFPCM with Weighted Mahalanobis Distance and repulsion is represented in Table 4.2. |
| The PSNR value of the proposed MFPCM with Weighted Mahalanobis and repulsion approach is observed to be very high when compared to the existing clustering techniques such as FPCM and MFPCM. For instance, the PSNR value of the proposed approach for the Peppers image is 39.98 dB which is very high when compared to the PSNR values of FPCM and MFPCM. |
| Figure 4.2 shows the comparison of the PSNR values of the proposed approach with the existing approaches. From Figure 4.2, it is observed that PSNR values of the proposed MFPCM with Weighted Mahalanobis Distance and repulsion approach is higher when compared to the FPCM and MFPCM techniques. |
| The PSNR values of the proposed approach obtained for the standard Lena, Cameraman and Peppers are 37.87, 38.94 and 39.98 respectively. Thus, it can be observed that the proposed approach produces better results than the existing methods in terms of PSNR values. |
CONCLUSION
|
| Efficient image compression techniques are becoming very vital in areas like pattern recognition, image processing, data mining etc. Image Compression is a technique of efficiently coding digital image to reduce the number of bits required in representing an image. Various image compression techniques are available in the literature but most of them posses certain limitations. This paper proposes a novel technique using VQ for effective image compression. |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
References
|
- Mei Tian, Si-welLuo and Ling-Zhi Liao, “An investigation into using singular value decomposition as a method of image compressions “,International Conference on Machine Learning and Cybematics, Pp. 5200- 5206, 2005.
- Xiao-Hong Wu and Jian-Jiang Zhou,”Possibilistic Fuzzy C-Means Clustering Model Using Kernal Methods “, International Conference onIntelligent Agents, Web Technologies and Internet Commerce, Vol.2, Pp.465-470, 2005.
- Yang Yan and Lihui Chen, “HypersphericalPossibilistic Fuzzy C-Means for high- dimensional data clustering”, ICICS 2009, 7th InternationalConference on Information, Communications and Signal Processing, Pp.1-5, 2009.
- VudaSreenivasarao and Dr. S. Vidyavathi, “Comparative Analysis of Fuzzy C – Means and Modified Fuzzy Possibilistic C- Mean Algorithmsin Data Mining”, IJCST Vol.1, Issue 1, Pp. 104-106, September 2010.
- R.Nagendran and P.ArokiaJansi Rani, “A novel FPCM based vector quantizer codebook design for image compression in the wavelet packetdomain”, The International Journal of Multimedia and its Applications, Vol.2, No.1,Pp.1-8,2010.
- Linde, A.Buzo and R.M.Grey, “An algorithm for vector quantizer design,” IEEE Transactions on Communication, Vol.28, No.1, Pp.84-95,1980.
- R.C. Gonzalez, R.E.Woods, Digital Image Processing, Pearson Education Pvt. Ltd., New Delhi, 2nd Edition.
- Z.M.Lu, J.S.Pan and S.H Sun, “Image Coding Based on classified sidematch vector quantization”,IEICE Trans. Inf. & Sys., Vol. E83-D(12),Pp.2189-2192, Dec.2000.
- Chun-Yang Ho, Chaur-Heh Hsieh and Chung-Woei Chao, “Modified Search Order Coding for Vector Quantization Indexes”, Tamkang Journalof Science and Engineering, Vol.2, No.3, Pp.143-148, 1999.
- R.M.Gray, “Vector quantization”, IEEE Acoustics, Speech and Signal Processing Magazine, Pp.4-29, 1984.
- M.Goldberg, P.R.Boucher and S.Shlien, “Image Compression using adaptive vector quantization, “IEEE Transactions on Communication,Vol.34, No.2, Pp.180-187, 1986.
- W.L.Hung, M Yang, D. Chen”, Parameter selection for suppressed fuzzy C-Means with an application to MRI segmentation”, PatternRecognition Letters 2005.
- K.Lung, “A cluster validity index for fuzzy clustering” Pattern Recognition letters 25, Pp. 1275-1291, 2005.
- S.Sathappan, S.Pannirselvam, “An enhanced vector Quantization method for Image Compression with Modified Fuzzy Possibilistic C – Meansusing Repulsion”, International Journal of Computer Applications, Vol. 21, No.5, Pp.27-34, May 2011.
- S.Mitra, R.Shuyu Yang Kumar, B.Nutter. “An optimized Hybrid Vector Quantization for efficient source encoding IEEE 2002, 45th MidwestSymposium, Vol. 2, 2002.
- Subramanya, “Image Compression Technique”, IEEE Potentials, Vol. 20, No.1, Pp. 19-23, 2001.
|