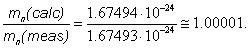About Mass of Neutron

Abstract

If to consider neutron as a composite particle consisting of proton and relativistic electron, it is possible to predict its magnetic moment, its mass and the energy of its decay, as well as the binding energy of neutron and proton in deuteron.

Keywords

Mass, Neutron, Relativistic electron, Magnetic moment.

Introduction

The electromagnetic model of neutron was considered earlier [1]. It assumes that neutron is a combined particle consisting of proton and rotating around it relativistic electron. Then some properties of neutron were calculated. This short article is devoted to the calculation of mass of neutron in the framework of this model.

The kinetic energy of a relativistic particle in the general case can be written as [2]:

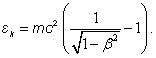(1)

Where 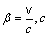is the light velocity, m is particle mass in the rest. The maximum kinetic energy of electron produced in the decay of neutron was calculated in (1):

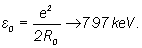
Where

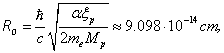
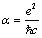is fine structure constant, 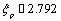is anomalous magnetic moment of proton m_eand M_p are masses of electron and proton in the rest.

Therefore, for electron that occurs at β-decay of neutron, considering (2) we obtain the equality:

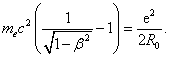
It follows from this equation that the mass m* of relativistic electron

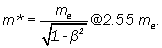
and mass of neutron:

m_n (calc) = m_p + m* ≅ 1.67494 • 10-24g. (6)

This value agrees very well with the measured value of the mass of neutron:

References

1. Vasiliev BV. About Nature of Nuclear Forces,Journal of Modern Physics. 2015; 6: 648-659.
2. Landau LD and Lifshitz EM. The Classical Theory of Fields,Pergamon Press. N.Y. 1971.