Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Adaptive Denoising of Impulse Noise with Enhanced Edge Preservation

P.Ruban1, M.P.Pramod kumar2
  1. Assistant professor, Dept. of ECE, Lord Jegannath College OfEngg& Tech, Kanyakumari, Tamilnadu, India
  2. PG Student [Applied Electronics], Lord Jegannath College Of Engg& Tech, Kanyakumari, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Image acquisition and transmission seems to be challenging when the images are corrupted by impulse noise. An efficient de-noising method for the removal of random valued impulse noise has been presented here including its VLSI architecture. The proposed method is a low complexity method which ensures low cost. The noisy pixels are detected by a Decision tree based impulse detector which is followed by an Edge preserving image filter which reconstructs their intensity values. The prominent feature is an adaptive technology which enhances the effect of de-noising. The proposed system beats the previous lower complexity methods in both quantitative evaluation and visual quality which is evident in the experimental results. Furthermore the performance of the proposed technique was found to be proportionate to the higher complexity methods. When it is about the design’s VLSI architecture, it yields a processing rate of about 200 MHz by using TSMC 0.18 μm technology. Also, a reduction in memory storage by more than 99 percent is obtained by this technology. The requirement of this design is limited to low complexity and need only two line buffers. Many real-time applications can adopt this design as its hardware cost is low.

Keywords
Random-valued impulse noise, Denoising, Decision tree based denoising method, Edge preserving image filter, Adaptive technology

INTRODUCTION
Several fields such as medical imaging, scanning techniques, printing skills, license plate recognition, face recognition, etc. make use of Image processing to a great extent. But the problem arises when the images are corrupted by impulse noise. The performance can be fatally affected by these noises. So, the importance of an efficient de-noising technique is a significant issue in image processing. Impulse noise can be classified into two, according to the distribution of noisy pixel values, such as: fixed valued impulse noise and random-valued impulse noise. In fixed valued, the pixel value of a noisy pixel is either minimum or maximum value in gray-scale images and is also known as Salt-and-pepper noise. The noisy pixel values in random-valued impulse noise are uniformly distributed in the range of [0, 255] for gray-scale images. Several methods are there for the removal of salt-and-pepper noise, and some of them perform very well. But random-valued impulse cannot be removed with much ease due to random distribution of noisy pixel values. In this paper, we focus only on the removal of random valued impulse noise from images.

RELATED WORK
There have been proposed many methods recently to carry out impulse noise suppression. The early methods include the standard median filter or its modifications. But the problem is that both noisy and noise-free pixels are modified resulting in a blurred image. An efficient switching strategy to avoid the damage on noise-free pixels has been proposed. It locates the noisy pixels with an impulse detector, and then filters them rather than the whole pixels of an image to avoid causing the damage on noise-free pixels. One method involves a novel adaptive operator, which forms estimates based on the differences between the current pixel and the outputs of center-weighted median (CWM) filters with varied center weights. Another category involves a generalized framework of median based switching schemes, called multi-state median (MSM) filter. By using simple thresholding logic, the output of the MSM filter is adaptively switched among those of a group of center weighted median (CWM) filters that have different center weights. Another algorithm is proposed based on the alpha-trimmed mean, which is a special case of the order statistics filter. Once a noisy pixel is identified, its value is replaced by a linear combination of its original value and the median of its local window. A differential rank impulse detector (DRID) also exists. The impulse detector of DRID is based on a comparison of signal samples within a narrow rank window by both rank and absolute value. The detector is based on a comparison of signal samples within a narrow rank window by both rank and absolute value. It is efficient, very fast, and can be used with any filter, without smoothing an image. There is another method which is using a statistic of rankordered relative differences (RORDWMF) to identify pixels which are likely to be corrupted by impulse noise. In this method, it is presented an efficient algorithm for the removal of random-valued impulse noise from a corrupted image by using a reference image. The proposed method uses a statistic of rank-ordered relative differences to identify pixels which are likely to be corrupted by impulse noise. Once a noisy pixel is identified, its value is restored by a simple weighted mean filter. A directional weighted median (DWM) method is another existing system. This method proposes a new impulse detector, which is based on the differences between the current pixel and its neighbours aligned with four main directions. Then, we combine it with the weighted median filter to get a new directional weighted median (DWM) filter. Another system proposed is that employed genetic programming for impulse noise filter construction which is based on the switching scheme with cascaded detectors and corresponding estimators.

PROPOSED SYSTEM
The proposed method is based on a novel adaptive decision-tree-based-denoising method. The decision tree is a logic which can be considered as a powerful form of multiple variable analysis. The idea includes the breakdown of a complex decision-making process into a collection of simpler decisions, thereby providing easier interpretation. The decision tree is a powerful The proposed system considers random-valued impulse noise with uniform distribution. 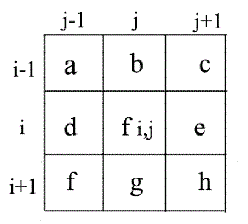The image denoising here uses a standard mask of 3 x 3. Consider the noisy pixel under consideration is located at coordinate (i, j) and denoted as p( i ,j ), whose luminance value is named as f(i ,j) , as shown in Fig. 1.
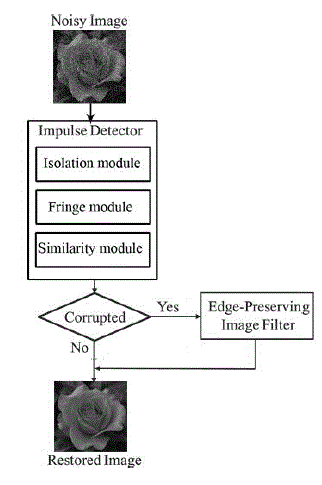
The remaining eight pixel values can be divided into two sets according to input sequence of images as: WTopHalf and WBottomHalf. The proposed DTBDM is a combination of two sections: decision-tree-based impulse detector and edgepreserving image filter. The decision regarding p (i, j) to be a noisy pixel is determined by the impulse detector by using the decision tree and the correlation between pixel p (i, j) and its neighbouring pixels. Positive result triggers edge-preserving image filter to generate the reconstructed value based on direction-oriented filter. Otherwise, the value will be kept unchanged.
Fig. 2 shows the design concept of the proposed DTBDM. The results of reconstructed pixels are adaptively written back as a part of input data in order to enhance the effects of removal of impulse noise. The hardware cost becomes low as the method uses only two line memory buffers. Thus for an grey scale test image having dimension 512x512, it is required only two line buffers like 512x2x8. Thus about 99.6 percent of storage is reduced. Another advantage of the DTBDM is that only simple arithmetic operations, such as addition and subtraction, are used. No previous training is required for the noises to be effectively removed. Our extensive experimental results demonstrate that the proposed technique can obtain better performances in terms of both quantitative evaluation and visual quality than other lower complexity denoising methods. Moreover, the performance can be comparable to the higher complexity methods. The seven-stage VLSI architecture for the proposed design was implemented and synthesized by using Verilog HDL and Synopsys Design Compiler, respectively. In our simulation, the circuit can achieve 200 MHz with only 21k gate counts by using TSMC 0:18 μm technology.

MODULE DESCRIPTION
A. Decision tree based impulse detector: The aim of the impulse detector is to find whether pi,jis a noisy pixel or not. This is usually made by considering the correlation between the neighbouring pixels. These methods when deeply observed can be classified into several ways according to degree of isolation at current pixel, in accordance with the pixel when comes on an edge, or with comparison of current pixel with neighbouring pixels. These classifications are physically implemented by designing three modules.
Isolation module (IM)
Fringe module (FM)
Similarity module(SM)
The decision tree is actually made through the concatenating decisions made by these three modules. It is actually a binary tree that uses the different equations in different modules to determine the status of pi,j. The isolation module is the foremost and is used to decide whether the pixel value is in a smooth region. A negative result will give the conclusion of the current pixel belongs to be noisy free. A positive result will give two inferences that the current pixel might be a noisy pixel or just situated on an edge. The next is the fringe module and is used to confirm any of the above result. The fringe module will give a negative result if the current pixel is situated on an edge and will give positive result otherwise. If the above two modules fail to determine whether current pixel belongs to noisy free, the similarity module is used to decide the result. This module compares the similarity between current pixel and its neighbouring pixels. Positive result confirms, pi,j to be a noisy pixel; and otherwise, it is noise free. The three modules are described in the following sections.
Isolation module: A smooth region can be characterized by having pixel values which should be close or locally slightly varying. So the difference between the pixel values will be minimal. The distribution of pixel values will be different if there are noisy values, edges, or blocks in this region. Thus the smoothness of the surrounding pixels is observed to determine whether the pixel is in an isolation point. The isolation point in a noisy image is defined by those pixels with shadow suffering from noise and so having low similarity with the neighbouring pixels. There will be a large difference between it and the neighbouring pixels.
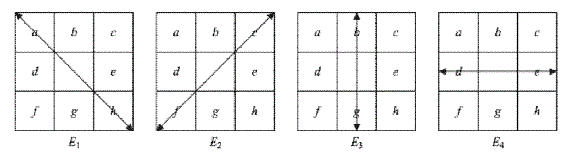
Fringe module: This module mainly deals with edge oriented decisions. Larger difference of neighbouring pixels with pi,jshows whether the pixel is noisy of situated on an edge. It is much difficult to make a conclusion regarding this. This situation can be better relieved by defining four directions, from E 1 to E 4, as shown in Fig. 3.We take direction E 1 for example. The absolute difference between fi,j and the other two pixel values along the same direction is found. Using this, we can determine whether the pixel is noisy or situated on an edge.
Similarity module: If isolation module and fringe module cannot determine whether current pixel belongs to noisy free, the similarity module is used to decide the result. The similarity between current pixel and its neighbouring pixels is compared. If the result is positive, pi,j is a noisy pixel; otherwise, it is noise free. The mask W located in a noisy-free area has luminance values that might be close. The median is always located in the center of the variational series, while the impulse is usually located near one of its ends. Thus we can check for extreme big or small values that implies the possibility of noisy signals. This can be attained by sorting nine values in ascending order and obtain the fourth, fifth, and sixth values which are close to the median in mask W. The fourth, fifth, and sixth values are represented as 4th in Wi,j, Median In Wi,j and 6th in Wi,j . Using these values we define two values such as Max i,j and Min i,j. and determines a noisy pixel.
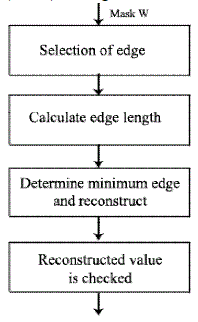
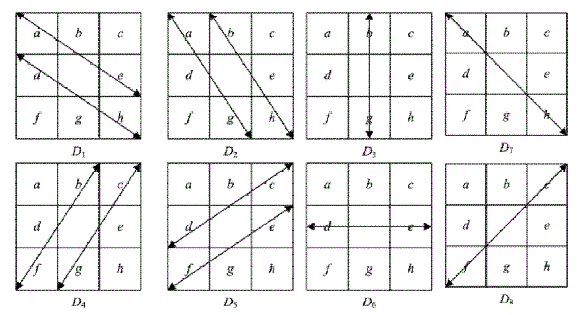
B. Edge-Preserving image filter: An edge-preserving technique is used to locate the edge existing in the current W. This can be easily realized using a VLSI circuit. Fig. 4 shows the dataflow of Edge-Preserving image filter. Eight directional differences, from D1 to D8 are considered, to reconstruct the noisy pixel value as shown in Fig.5. Possible misdetection is avoided by considering only those composed of noise-free pixels and considering only directions passing through the suspected pixels. To determine whether the values of d, e, f, g, and h are corrupted, we use Max i,j and Min i,j, defined in similarity module. The direction including the suspected pixel is not considered if the pixel is likely being corrupted by noise. No edge can be processed if all the pixels are suspected to be noisy. In such situation, fi,j(the estimated value of pi,j) is equal to the weighted average of luminance values of three previously denoised pixels and calculated as (a + b x 2 + c) / 4.In other conditions, the edge filter calculates the directional differences of the chosen directions and locates the smallest one ( D min) among them in the third block.

RESULT AND DISCUSSION
For the evaluation process a test image Rose is simulated using the proposed system as well as some standard low complexity and high complexity methods and the results are compared. In the experimental results, it is evident that the quantitative qualities of DTBDM are always better than those lower complexity methods in low noise ratio and almost the same with other higher complexity methods. The memory requirement and computational complexity determines the cost of VLSI implementation. Only few computations are required in the proposed system. Thus, the low cost is proven by line buffer and iteration times. As demonstrated, DTBDM requires lower hardware cost and works faster than most of the other methods. Even if the proposed method requires more logic elements than some methods, it can achieve higher frequency and produce better image quality when denoising an image corrupted by random valued impulse noise. The output of proposed system is shown in Fig.6.
The output of the proposed system is demonstrated by denoising a standard test image which is a 512x512 8-bit grayscale image. For that, the corrupted version of the test image is generated in Matlab environment with random valued impulse at noise intensity of 20 percent. Then we employ the proposed system to detect the presence of noise and restore the corrupted image. The output image shows the efficiency of the proposed system in removing random valued impulse noise. It can be theoretically confirmed by finding out the PSNR value which is obtained as 34.79 which is considerably higher than the compared lower complexity methods and is comparable to higher complexity methods
The comparison of the results with some of the lower complexity methods is shown in the Table 1. Here, six methods Median, ACWM, RVNP, ATMBM, DRID, RORD-WMF and the proposed system(DTBDM) are compared. The standard peak signal-to-noise ratio is employed to illustrate the quality of the reconstructed image for various methods. The table shows the restoration results in PSNR (db) of the test image corrupted by 5, 20 percent impulses respectively. Among the methods, the first three belong to lower complexity methods and perform no iteration. The other three belong to higher complexity methods which involve complex methods of operations and iterations. The results of the experiment mentioned in the table clearly shows that the proposed system gives better quality than the compared lower complexity methods and almost the same with the higher complexity methods.

CONCLUSION AND FUTURE WORK
The experimental result demonstrate that the performance of our proposed technique is better than the previous lower complexity methods and is comparable to the higher complexity methods in terms of both quantitative evaluation and visual quality. The VLSI architecture of our design yields a processing rate of about 200 MHz by using TSMC 0:18 μm technology. It requires only low computational complexity and two line memory buffers. Therefore, it is very suitable to be applied to many real-time applications.
The present system deals with the impulse noise removal technique which is of low cost with minimum device utilization. In future, retaining these qualities it can be further modified. The mask size which is critical can be increased from 3x3 to 5x5 without increase in considerable amount of additional memory. This will give more information about the noise amount and can correct the noise with much precision. Also the directional differences taken in the edge-preserving filter can be increased to many times when compared with the present system and it will give considerable amount of improvement in the noise detection and removal.

ACKNOWLEDGEMENT
I take immense pleasure in expressing our humble note of gratitude to my guide Mr.RUBAN.P, ME., Assistant Professor, Department of Electronics and Communication Engineering, for his remarkable guidance in the course of completion of this paper. I also extend my sincere thanks to Mr. Y. SINGSTON ALBERT DHAS, ME Head of Department, Department of Electronics and Communication Engineering, for the support and timely assistance rendered for this project to have come out in flying colors.
 

Tables at a glance
Table icon
Table 1
 

Figures at a glance


Figure Figure Figure
Figure 1 Figure 2 Figure 3
Figure Figure Figure
Figure 4 Figure 5 Figure 6
 

References