INTRODUCTION
|
| Optical networks are high capacity telecommunication networks based on optical technologies and components that provide routing, grooming and restoration at the wavelength level as well as wavelength based services. Optical networks, based on the emergence of the optical layer in transport network, provide higher capacity and reduced cost for new applications such as the internet, video and multimedia interactions and advanced digital services. |
| Burst switching in a packet switched network, burst switching is a capability in which each network switch extracts routing instructions from an incoming packet header to establish and maintain the appropriate switch connection for the duration of the packet, following which the connection is automatically released. In concept, burst switching is similar to connectionless mode transmission, but differs in that burst switching implies intent to establish the switch connection in near real time so that only minimum buffering is required at the node switch. A variant of burst switching used in optical networks is optical burst switching. |
| An OPS is another switching paradigm that allows packet switching and routing in optical domain without conversion to electronics at each node. In OCS networks dedicated WDM channels or light paths are established between a source and destination pair. |
| In optical burst switching (OBS) bursts and control packets (CP) are transported. The packets are assembled into bursts at an ingress node. The CP is a heard packet and includes such burst information as wavelength, burst length, and offset time. This information is used for resource reservation at core nodes. The CP is sent before the corresponding burst in order to reserve wavelength. Wavelength is reserved at core nodes along a path to forward bursts. At the core node, the CP over a control wavelength is converted to an electronic signal in order to reserve wavelength and is then reconverted to an optical signal. This optical-electronic-optical (OEO) conversion causes processing overhead. On the other hand, bursts are sent as an optical signal along a path without using an OEO converter. Because of the difference in the processing of the CP and burst at core nodes, the CP must be transmitted before the burst at the ingress node considering the CP processing times at core nodes along a path. This time period between the CP and burst transmissions at the ingress node is called the offset time. |
| The offset time must be longer than the sum of the CP processing times at all core nodes along a path. If the offset time is shorter than the sum of the CP processing times, the burst arrives at a core node before the CP arrives and is discarded because a wavelength is not reserved. |
ADAPTIVE OBS
|
| A. Network architecture |
| A specific wavelength is dedicated to the control plane, the corresponding traffic being processed electronically at each node. All other wavelengths are dedicated to the user plane; the corresponding traffic is optically switched, without any OEO conversion, from source to destination .Each fiber can carry a limited number of wavelengths. Edge nodes communicate with each other via optical bursts that may be routed through intermediate nodes and span multiple links. Several optical bursts can be simultaneously transmitted over the same link as long as they use different wavelengths. In the absence of wavelength converters, the optical bursts must use the same wavelength on all links on their path from the source to the destination. |
| B. Reservation scheme |
| When a source-destination (SD) pair has one burst ready for trans- mission, it becomes active and attempts to reserve an optical connection, we refer to as lightpath. Specifically, each SD pair has some predefined set of eligible paths in the network. At each reservation attempt, the source selects a subset of these paths and sends a request control packet on each of these paths. The request control packets collect the state of wavelengths on their way to the destination. Based on the data contained in the request control packets, the destination selects one of the available paths, if any. It then sends back a reserve control packet on the chosen path which is destined to reserve the optical resources at intermediate nodes. When the source receives the reserve control packet, it can immediately transmit data on the specified lightpath. If no lightpath is available, the destination sends a failure control packet to inform the source of the occupancy of the optical resources, the source then reattempts a reservation |
| C. Assembly mechanism |
| At each source, incoming data packets are electronically buffered according to their destination. These packets are then assembled into bursts that are characterized by some minimum size compatible with the switching capability of core optical nodes. Unlike conventional OBS, in which the size of the burst is insensitive to the traffic conditions, adaptive OBS allows the source to dynamically adjust the size of the burst to the network load. We use the number of active data flows as a measure of network congestion. Specifically, the size of the burst sent by any SD pair is equal to the minimum burst size, say B, multiplied by the number of active data flows on this SD pair at the reception of the reserve control packet. A data flow here refers to any instance of application and is typically identified through the usual 5- uple of the IP header: source and destination IP addresses, source and destination ports, and protocol. |
STABILITY ANALYSIS
|
| A. Network model |
| Let L be the number of links and Wl the number of data wavelengths of link l (excluding the control wavelength). There are K source-destination (SD) pairs in the network. Each SD pair k is characterized by some set of eligible pathsin the network. Path j of SD pair k is defined by some subset of links, pkj ⊂{ 1,...,L}. Any burst transmission requires the prior reservation of some path from the source to the destination. Each reservation takes one round-trip time, denoted by δkj for SD pair k on path j. We consider the general case where SD pair k runs Nk reservation processes in parallel and can thus transmit up to Nk bursts simultaneously, (possibly on the same path, using different wavelengths). The source must then be equipped with at least Nk tunable transmitters. |
| We consider two types of networks, depending on the technology of the underlying optical switches: |
| • Wavelength conversion: A lightpath can use any available wavelength on each link. In particular, there is no need to specify the allocated wavelengths. The network state at time t is then described by some vector y(t) whose component kj corresponds to the number of lightpaths reserved for SD pair k on path j at time t. The capacity contraints are given by: |
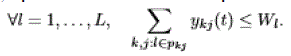 |
| • No wavelength conversion: A lightpath must use the same wavelength from the source to the destination. To ensure connectivity, we then assume that all links have the same number of wavelengths, denoted by W. The network state at time t is described by some vector y(t) whose kjw component is equal to 1 if some lightpath is reserved for SD pair k on path j and wavelength w at time t, and is equal to 0 otherwise. We still denote by ykj(t)= W w=1 ykjw(t) the number of lightpaths reserved for SD pair k on path j at time t. Since a wavelength cannot be allocated to more than one SD pair, the capacity constraints become: |
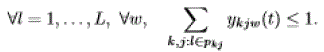 |
| • In both cases, the total number of reserved lightpaths of SD pair k, say yk(t)= j ykj(t), cannot exceed Nk. We denote by Y the set of feasible states, that satisfy this constraint and depending on the considered network. Let R be the optical line rate of each wavelength, in bit/s. The average throughput of SD pair k when state y is selected with probability π(y) is given by: |
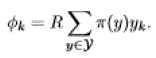 |
| φ the corresponding vector and refer to the capacity region as the set of vectors φ generated by all probability measures π on the set Y. This defines the set of all throughput vectors that can be allocated to the SD pairs . |
| B. Resource allocation |
| Let xk be the number of active flows on SD pair k; the pair becomes active as soon as xk > 0. Whenever active, source k runs Nk reservation processes in parallel. Each process attempts to reserve a lightpath after some exponential |
| backoff time of parameter ν. For simplicity, we assume1 that a single path is attempted at random. Specifically, path j is attempted with probability αkj > 0, with j αkj =1. In the absence of wavelength conversion, we assume that a single wavelength is attempted at random. If the reservation is successful, source k sends a burst of length xkB, where B denotes the minimum burst size (in bits); otherwise, it reattempts a reservation after a new exponential backoff time of parameter ν. |
| As mentioned above, we neglect the phenomenon of back- ward blocking. Specifically, we assume that the reservation of source k starting at time t is successful if and only if the vector y(t)+ekj satisfies the capacity constraints (1) in case of wavelength conversion, or the vector y(t)+ekjw satisfies the capacity constraints (2) in the absence of wavelength conver- sion, where w denotes the attempted wavelength and ekj,ekjw are the corresponding unit vectors of Y. The network state then changes instantaneously at time t, the actual transmission starting at time t + δkj for xkτ time units, where τ = B/R denotes the transmission time of a burst of minimum size. Under the above assumption, the reservation processes behave as a multiclass loss network of Engset type with class- k customers representing the Nk reservation processes of SD pair k. The associate stationary measure in state x is given by : |
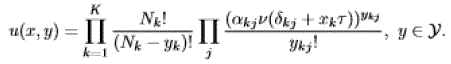 |
| We obtain the stationary distribution of the resource allocation y in state x by normalization: |
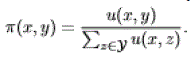 |
| By the insensitivity property , this stationary distribution is independent of the distribution of the backoff times beyond the mean, provided the latter has a continuous, infinite support. |
| C. Flow-level dynamics |
| Assume that data flows arrive according to a Poisson process of intensity λk > 0 at SD pair k and have exponential2 flow sizes of mean σk bits. We denote by ρk = λkσk the traffic intensity of pair k in bit/s and by ρ the corresponding vector. Let x(t) be the network state (in terms of the number of flows on each SD pair) at time t. Assuming that the flow time- scale is much slower than the burst time-scale, the throughput of SD pair k in state x is given by: |
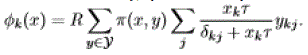 |
| The network state x(t) then corresponds to that of a system of K coupled queues with arrival rates λk and service rates φk(x)/σk. We say that the network is stable if the underlying Markov process is ergodic, meaning that the number of active flows on each SD pair achieves a stationary regime. We have the following key result, showing the optimality of adaptive OBS in terms of resource allocation: |
| The network is stable whenever the vector ρ of traffic intensities lies in the interior of the capacity region. |
| If the vector of traffic intensities lies in the interior of the capacity region, there exist some >0, and some probability measure π on Y such that: |
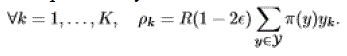 |
| Note that we can choose π(y) > 0 for all y ∈Y . |
| Define: |
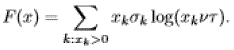 |
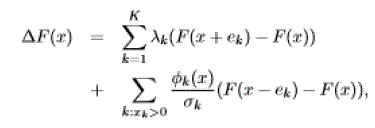 |
| satisfies ΔF(x) ≤−α in all states x but some finite number. Using the convention 0log(0) ≡ 0, we have: |
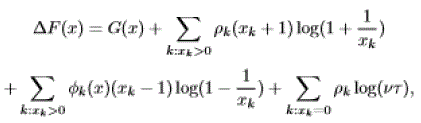 |
| with: |
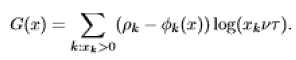 |
| using (4) and (5) |
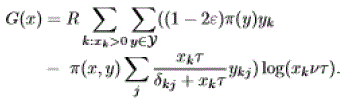 |
| Let: |
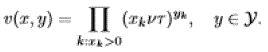 |
| using the fact that: |
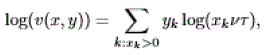 |
| In view of Lemma 1, we have for all states x but some finite |
| Since v(x,y) ≤ v(x) for all states x, the second term is non- positive and we deduce that for all states x but some finite number: |
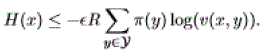 |
| Since π(y) > 0 for all y ∈Y, this expression tends to −∞ when |x| = ??k xk tends to +∞. The differences ΔF(x) − G(x) and G(x)−H(x) being upper bounded, we deduce that there exists α>0 such that ΔF(x) ≤−α for all states x but some finite number. |
PERFORMANCE RESULTS
|
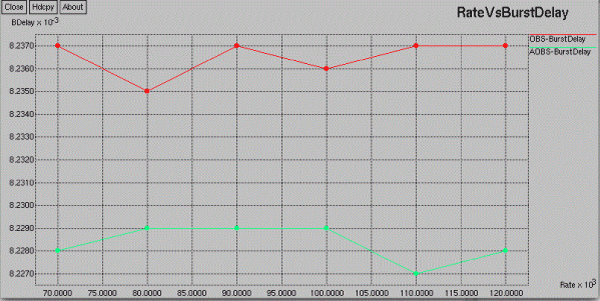
| I am comparing the performance of AOBS and OBS in terms of Burst Delay, Burst Drop, Blocking probability, Burst Received, Delay and Packets Received. Following are the graphical representation of obtained output |
| RATE VS BURST DELAY |
 |
| RATE VS BURST DROP |
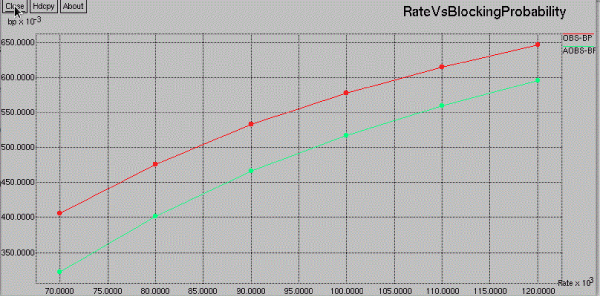 |
| RATE VS BLOCKING PROBABILITY |
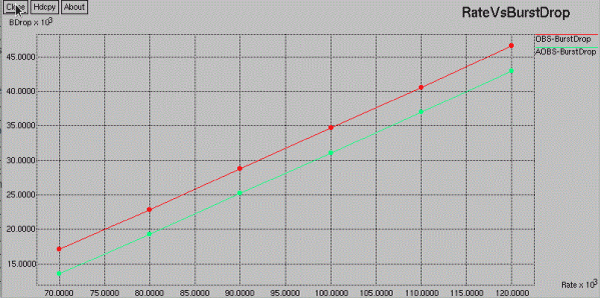 |
CONCLUSION
|
| Unlike conventional OBS, in which the size of the burst is insensitive to the traffic conditions, adaptive OBS allows the source to dynamically adjust the size of the burst to the network load. We use the number of active data flows as a measure of network congestion. Specifically, the size of the burst sent by any SD pair is equal to the minimum burst size, say B, multiplied by the number of active data flows on this SD pair at the reception of the reserve control packet. A data flow here refers to any instance of application and is typically identified through the usual 5- uple of the IP header: source and destination IP addresses, source and destination ports, and protocol. |
| |
References
|
- C.Qiao and m.yoo, “optical burst switching (OBS) – A new paradigm for an optical internet,”journal of high speed networks,vol.8, pp.69- 84,1999.
- “Service Differentiation in Optical Burst Switching Networks”,christophauger,Klausdolzer,janspath,Stefanbodamer university of Stuttgart,institute of communication networks and computer engineering(IND)
- “Improvement of Burst Transmission Delay using Offset Time for Burst Assembly in Optical Burst Switching”,taiju MIKOSHI and toyofumiTAKENAKA.
- TI. Baldine, H.l, G. Perros, G. Rouskas, and D. Stevenson, “JumpStart: A Just-in-Time signaling architecture for WDM burst-switched networks,” IEEE Communications Magazine, vol. 40, pp. 82–89, 2002.
- T. Bonald, R.-M. Indre, S. Oueslati, and C. Rolland, “On virtual optical bursts for qos support in obs networks,” in Proc. of ONDM, 2010.
|