Keywords
|
| Field Programmable Gate Array (FPGA), Arithmetic Logic Unit (ALU), Floating point, IEEE754 |
INTRODUCTION
|
| In computing, floating purpose describes a system for representing real numbers that supports a wide vary of values. Whereas fashionable supercomputers rely virtually exclusively on a set of ancient microprocessors, these microprocessors have poor sustained performance on several modern scientific applications [1]. FPGAs could offer associate degree alternative, however scientific applications rely on IEEE compliant floating-point computations for numerical stability and dependability of results. Will increase in FPGA density, and optimized floatingpoint unit styles, have created it doable to implement a range of scientific algorithms with FPGAs [2], [3], [4]. Numbers are generally diagrammatical some to a hard and fast range of serious digits and scaled victimization a fan. The bottom for the scaling is often two, 10 or 16. The everyday range that may be diagrammatical specifically is of the form: Significant digits × base exponent. The term floating purpose refers to the very fact that the base purpose will "float". |
| It is placed anyplace relative to the numerous digits of the quantity. This position is indicated on an individual basis within the internal illustration, and floating-point illustration will so be thought of as a laptop realization of scientific notation. Over the years, many totally different floating-point representations are employed in computers. For the last 10years the foremost usually encountered illustration is that outlined by the IEEE 754 customary. The advantage of floatingpoint illustration over fixed-point illustration is that it will support a way wider vary of values. For example, a fixedpoint illustration that has seven decimal digits with 2 decimal places, will represent the numbers 12345.67, 123.45, 1.23 and then on, whereas a floating-point illustration with seven decimal digits might additionally represent one.234567, 123456.7, 0.00001234567, 1234567000000000, and so on. The floating-point format wants slightly additional storage, therefore once keep in the same house, floating-point numbers succeed their larger vary at the expense of exactness. The speed of floating-point operations is associate degree important live of performance for computers in several application domains. |
RELATED WORKS
|
| The following paper that deals with a design for a reconfigurable device that's specifically optimized for floating purpose applications. Fine grained units are used for implementing management logic and bit-oriented operations. Coarse grained units incorporating word-oriented search tables and floating purpose operations are wont to implement information methods. Comparison with existing FPGA devices, the virtual embedded block theme is planned to model embedded block victimization existing Field-Programmable Gate Array (FPGA) tools. In this thesis the Floating purpose embedded processor is proposed. This Floating purpose embedded processor performs the several operations such as Fp-addition, Fp-subtraction, Fp-multiplication, Fp-division, Fp-trigonometric, Fplogical operations. The most objective is to style and develop totally pipelined embedded processor victimization IEEE 754 format. The Floating purpose processor is intended by victimization IEEE 754 single precision format. The IEEE 754 commonplace defines 5 sorts of exceptions like Invalid operation, Division by zero, Inexact, Underflow, Overflow, Infinity, and Zero. There are few papers mentioned to upset optimization techniques. ChiWai Yu planned a methodology to optimize coarse-grained floating purpose units (FPUs) in a very hybrid field-pro-gram ready gate array (FPGA).By using common sub graph extraction to work out the simplest mixture of blocks inside an FPU and study the realm, speed and utilization trade off over a collection of floating purpose benchmark circuits. Then explore the system impact of FPU density and suppleness in terms of space, speed, and routing resources. Finally, derive AN optimized coarse-grained FPU by considering each study and system-level issues. This planned methodology may be wont to judge a variety of FPU design optimizations [7]. |
| P. H. W. Leong planned the design for a reconfigurable device that is specifically optimized for floating-point applications. Fine-grained units are used for implementing management logic and bitoriented operations. In order to facilitate comparison with existing FPGA devices, the virtual embedded block theme is proposed to model embedded blocks victimization existing Field- Programmable Gate Array (FPGA) tools. This technique involves adopting existing FPGA resources to model the dimensions, position, and delay of the embedded components [8]. Then M. J. Beauchamp planned the strategy considering 3 study modifications that build floating-point operations additional economical on FPGAs. The initial modification embeds floatingpoint multiply-add units in AN island-style FPGA. Whereas giving a dramatic reduction in space and improvement in clock rate, these embedded units are a major modification and should not be even by the market. |
| The next 2 modifications target a major component of IEEE compliant floating-point computations: variable length shifters. These shifters provide a vital reduction in space with a modest increase in clock rate [9].The next paper that could be a novel methodology to optimize Coarse-grained floating purpose units (FPUs) in a very hybrid FPGA. We use common sub graph extraction to work out the number of floating purpose adders/subtracters (FAs), multipliers (FMs) and word blocks (WBs) within the FPUs. The results show that: (1) embedding additional sorts of coarse grained FPU within the system causes at the most twenty one.3% increase in delay, (2) the realm of the system may be reduced by twenty seven.4% by embedding high density sub graphs, (3) the high density sub graphs needs fourteen. 8% fewer routing resources [10].The next paper introduces Floating Point arithmetic is complex quantity arithmetic for activity numerical calculations on fashionable computers. |
| The advantage of floating-point illustration over fixed-point and number representation is that it will support a lot of wider vary of values. Addition/subtraction, Multiplication and division are the common arithmetic operations in these computations. |
| Among them Floating purpose Addition/Subtraction is that the most advanced one. This paper implements AN economical 32bitfloating purpose adder consistentwith IEEE754 commonplace with optimum chip space a nd high performance victimization Verilog HDL. |
| The planned design is enforced on Q II machine. Results of planned architecture are compared with the existed design and have observed reduction in space and delay [11]. E. Quinn ell planned a bridge consolidated multiplyadd unit could be a style supposed to feature FMA practicality to existing floating-point coprocessor units by as well as specialized hardware that reuses floating-point adder and floating-point multiplier factor parts. The bridge unit adds this practicality while not requiring AN overhaul of coprocessor management units and while not degrading the performance or Parallel execution of addition and multiplication single directions. To judge the performance, area, and power prices of adding a bridge FMA unit to common floating-point execution blocks, many circuits as well as a double-precision floating-point adder, floating-point multiplier factor, classic FMA, and a bridge FMA unit have been designed and implemented with AMD 65-nm silicon-on-insulator technology [12]. The Floating purpose embedded processor is developed once that optimization is finished. The VHDL cryptography for Floating purpose operation is developed. |
FLOATING POINT ARCHITECTURE
|
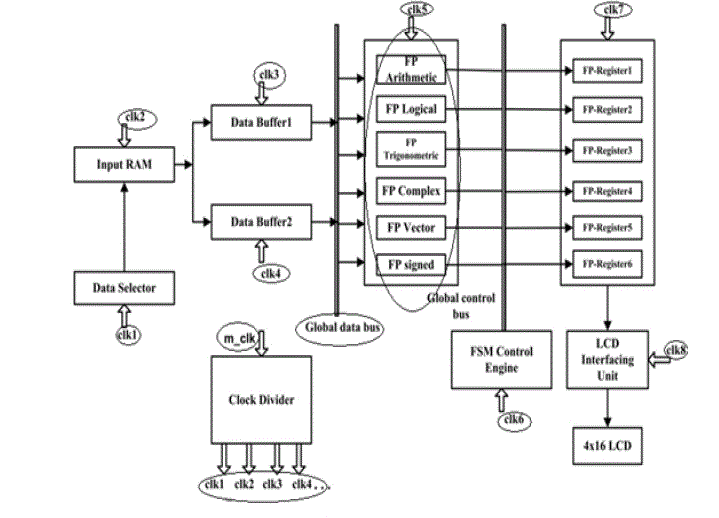
| The Floating purpose Embedded Processor having the subsequent structure that having the many blocks like knowledge selector, Input RAM, knowledge buffer, FP Operation block, FP Register, FSM management Engine, digital display Interfacing Unit, Clock divider, 4x16 LCD. |
| The input is given to the Input RAM. The info selector which gives the input to the RAM. Knowledge buffer that is that the temporary storage won’t to store the info that ought to be taken from the RAM memory. The 2 inputs that is hold on within the Data buffer. The input data’s ought to be hold on within the knowledge buffer up to that ought to tend to the FP Operation block. The FP Operation block performs many operations in same processor itself. The varied Operations are FP-Arithmetic, FPLogical, FP-Trigonometric, FP-Signed and FP-Unsigned Operation. |
| In the FP Operation performs the many operations within the FP Operation block. Once the operation is performed then it’s given to the FP Register block. The output ought to be taken from the FP Register with the assistance of FSMmanagement engine. Supported the FSM state the varied output is showed within the digital display display. The clock divider having the master clock frequency. The clock is split the clock signal is given to the every and each block. The represented illustration of the planned system is shown within the figure1.A. Input RAM Random-access memory may be a style of laptop knowledge storage. A random-access device permits hold on knowledge to be accessed directly in any random order. Then the inputs are given to the data buffer that may be a temporary storage. In distinction to alternative data storage media devices such as exhausting disks, CDs, DVDs and memory device, similarly as early primary memory sorts such as dram memory, scan and write knowledge solely in a preset order, consecutively, attributable to mechanical design limitations. Therefore, the time to access a given knowledge location varies considerably counting on its physical location. |
| The input RAM that is that the knowledge storage won’t to store the inputs which are used for the FP Operation. The inputs are hold on within the input RAM.B. Knowledge Selector Data Selector takes one knowledge input and variety of choice inputs, and that they have many outputs. They forward the info input to 1 of the outputs counting on the values of the selection inputs. Knowledge selector may be a device that selects one in all several analog or digital input signals and forwards the chosen input into one line. Knowledge selector that selects the inputs from the input RAMS. The info selector which supplies inputs to the RAM memory. |
IEEE 754 FLOATING POINT
|
| The real numbers portrayed in binary format square measure called floating purpose numbers. Supported IEEE-754 normal, floating point formats square measure classified into binary and decimal interchange formats. IEEE floating purpose numbers have 3 basic components: the sign, the exponent, and the mantissa. The mantissa consists of the fraction associate degreed an implicit leading digit. In general, floating purpose arithmetic implementations involve process severally the sign, exponent and fixed-point part parts, and then combining them when rounding error and normalization. IEEE normal for floating purpose IEEE-754 defines a binary format used for representing floating purpose numbers [5], [6]. |
| A number is portrayed by the triple field. |
EXPERIMENTAL RESULTS
|
| The Floating purpose processor performs the many operation during a same processor itself. The most objective is to style and develop a totally pipelined and optimized design. 1st the Floating purpose processor is developed. Then the optimization is finished. Optimization shows that they have the benefits of improved space, area-delay product, and throughput. The Floating-Point operation is performed by written code for machine operation in Verilog HDL. Then we tend to get the simulation result. The simulation done with the help of Altera quartus II and MODELSIM. The simulation result shows the result for Floating-Point operation. The machine operation performs the many operation like FP-Addition, FP-Subtraction, FP-Multiplication, FP-Division, FP Trigonometric,FP-Logical, FP-Complex operations. The 2 inputs area unit given then got the result for the actual inputs. The VHDL committal to writing for floating purpose operation victimization single exactitude format is developed. The assorted simulation results for various inputs area unit given below. |
| Two events cause the underflow exception to be signaled, tininess and loss of accuracy. Diminutiveness is detected when or before rounding once a result lies between ±2Emin. Loss of accuracy is detected once the results merely inexact or only a renormalizations loss happens. The implementer has the selection to choose however these events are detected. They ought to be an equivalent for all operations. The enforced FPU core signals associate underflow exception whenever diminutiveness is detected when rounding and at an equivalent time the results inexact. |
| 1) Overflow: The overflow exception is signaled whenever the result exceeds the utmost worth which will be described owing to the restricted exponent vary. it's not signaled once one among the operands is time, as a result of time arithmetic is often precise. Division by zero additionally doesn’t trigger this exception. |
| 2) Infinity: This exception is signaled whenever the result's time without reference to however that occurred. This exception isn't defined within the commonplace and was intercalary to sight quicker time results. |
| 3) Zero: This exception is signaled whenever the result is zero without reference to however that occurred. This exception isn't defined within the commonplace and was intercalary to sight quicker zero results. |
| In arithmetic, a division is termed a division by zero if the divisor is zero. Such a division will be formally expressed as a/0 where is that the dividend. Whether or not this expression will be assigned a well-defined worth depends upon the mathematical setting. In normal (real number) arithmetic, the expression has no which means. |
| In programming, number division by zero could cause a program to terminate or, as within the case of floating purpose numbers, could lead to a special not-a-number worth. The division of any range by zero apart from zero itself offers time as a result. The addition or multiplication of 2 numbers may offer time as a result.Representation of Double Precision Floating Point Number |
| Step 1: Convert Decimal to Binary |
| (12.375)10 -------- (1100.011)2 |
| Step 2: Shift the Decimal Point towards the Right side Till Getting the Leading Bit 1 1.100011X23 |
| Step 3: Obtain the Sign bit, Mantissa and Exponent from the above |
| S=0; E=e+1023; M=10001100000000000000…000 Step |
| 4: Represent the Same in IEEE 754 format |
CONCLUSION
|
| The Floating purpose Embedded Processor performs many operations such as FP-Addition, FP-Subtraction, FPMultiplication, FP-Division, FP-Logical, FP-Trigonometric, FP-Vector. The secret writing for Floating purpose embedded processor was developed and simulated. Floating purpose Embedded Processor having the advantage as giant dynamic ranges, less development time and a fewer cycles to execute than a set purpose. The design is meant and so improvement is completed. The applications of Floating purpose embedded processor square measure Modems, Digital Subscriber Line(SCL),home office switches, 3D Graphics, Speech Recognition, Digital Imaging, Military measuring instrument, Mobile TV, Automatic echo canceller in handsfree transportable device, skilled Audio result Processor, complicatedsystems in communication, Medical. Floating purpose Embedded Processor having the advantage as giant dynamic ranges, less development time and a fewer cycles to execute than a set purpose. Floating purpose processors a lot of easier to program in assembly code .I had developed the FP-Operation, the secret writing is written in VHDL and simulated. We actually have to optimize the design and implementing it on FPGA. |
| |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2&3 |
Figure 4&5 |
|
| |
References
|
- K. D. Underwood. FPGAs vs. CPUs: Trends in Peak Floating- PointPerformance. In Proceedings of the ACM International Symposium on Field Programmable Gate Arrays, Monterey, CA.
- K. S. Hemmert and K. D. Underwood. An Analysis of the Double-Precision Floating-Point FFT on FPGAs. In Proceedings of the IEEE Symposium on FPGAs for Custom Computing Machines, NapaValley, CA 2005.
- M. de Lorimier and A. DeHon. Floating point sparse matrix-vectormultiply for FPGAs. In Proceedings of the ACM International Symposium on Field Programmable Gate Arrays, Monterey, CA,February 2005.
- J. Liang, R. Tessier, and O. Mencer, “Floating point unit generation and evaluation for FPGAs,” in Proc. FCCM, Apr. 2003, p. 185.
- Gaffar,W. Luk, P. Cheung, and N. Shirazi, “Customising floating-point designs,” in Proc. FCCM, Apr. 2002, pp. 315–317.
- A. Gaffar, O. Mencer, W. Luk, and P. Y. K. Cheung, “Unifying bitwidth optimisation for fixed-point and floating-point designs,” in Proc.12th Annu. IEEE FCCM, 2004, pp. 79–88.
- Gaffar, O. Mencer,W. Luk, P. Cheung, and N. Shirazi, “Floating-point bitwidth analysis via automatic differentiation,” in Proc. EEE Int. Conf. FPT,Dec. 2002, pp. 158–165.
- F. Fang, T. Chen, and R. Rutenbar, “Floating-point bit-width optimization for low-power signal processing applications,” in Proc. IEEE ICASSP,2002, vol. 3, pp. III-3208–III-3211.
- G. Leyva, G. Caffarena, C. Carreras, and O. Nieto-Taladriz, “A generator of high-speed floating-point modules,” in Proc. 12th Annu. IEEESymp.FCCM, 2004, pp. 306–307.
- Z. Baidas, A. Brown, and A. Williams, “Floating-point behavioral synthesis,”IEEE Trans. Comput.-Aided Design Integr. Circuits Syst., vol. 20,no. 7,pp. 828–839, Jul. 2001.
- W. Geurts, F. Catthoor, and H. D. Man, “Quadratic zero–one programmingbased synthesis of application specific data paths,” in Proc. ICCAD,Nov.1993, pp. 522–525.
- J. Um, J. Kim, and T. Kim, “Layout-driven resource sharing in high-levelsynthesis,” in Proc. ICCAD, Nov. 2002, pp. 614–618.
|