Keywords
|
| Boolean function, fixed degree polynomial, algebraic normal form, numerical normal form |
INTRODUCTION
|
| Vectorial Boolean Functions for Cryptography which follows, the set {0, 1} will be most often endowed with the structure of field (and denoted by F2), and the set F2n of all binary vectors of length n will be viewed as an F2- vectorspace. We shall denote simply by 0 the null vector in F2n. The vectorspace F2n will sometimes be also endowed with the structure of field { the field F2n (also denoted by GF(2n)) [1]; indeed, this field being an n-dimensional vectorspace over F2, each of its elements can be identified with the binary vector of length n of its coordinates relative to a fixed basis. The set of all Boolean functions f : F2n-> F2 will be denoted as usual by BFn. The Hamming weight wH(x) of a binary vector x ε F2n being the number of its nonzero coordinates, the Hamming weight wH(f) of a Boolean function f on F2n is the size of the support of the function , i.e. the set {x ε F2n / f (x) ≠ 0}. The Hamming distance dH(f, g) between two functions f and g is the size of the set {x ε F2n / f (x) ≠ g(x)} . Thus it equals wH(fΘg). |
| Some additions of bits will be considered in Z (in characteristic 0) and denoted then by +, and sometimes will be computed modulo 2 and denoted by Θ . These two dierent notations will be necessary because some representations of Boolean functions will live in characteristic 2 and some representations of the same functions will live in characteristic 0. But the additions of elements of the finite field F2n will be denoted by +, as it is usual in mathematics. So, for simplicity (since F2n will often be identified with F2n) and because there will be no ambiguity, we shall also denote by + the addition of vectors of F2n when n > 1. |
| Many constructions of Boolean functions with properties relevant to cryptography are recursive [2, 4, 5,]. The efficiency of the constructions relies heavily on the use of appropriate functions of small dimensions. Another important method for construction is the random and heuristic search approach [2, 3]. As equivalence classes are used to provide restricted input of such optimization algorithms, it is very important to identify which equivalence classes obtain functions with desired properties. Methods bounding the degree of polynomial that present boolean functions have been important tools in complexity theory. These techniques have been uesd to obtain several results that shed light on the complexity of boolean functions. In particular, such polynomial degree lower bounds consequences for the constant-depth circuit complexity of the associated boolean functions. |
| Let the Boolean function written vector of its values with N = 2n coordinates, where n - number of variables of the function. It is known that the values vector of a Boolean function of a polynomial can be found with complexity O (N logN) [7]. Therefore, in finding algorithms that recognize properties of Boolean functions polynomials by their values vectors, it makes sense consider only algorithms that have lower order of complexity. In this paper we propose a linear complexity algorithm which determines the vector values a Boolean function given, it is a polynomial of fixed degree, and if so constructing this polynomial. |
REPRESENTATION OF BOOLEAN FUNCTIONS
|
| Among the classical representations of Boolean functions, the one which is most usually used in cryptography and coding is the n-variable polynomial representation over F2, of the form: |
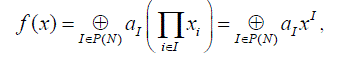 (1) (1) |
Where P(N) denotes the power set of N = {1, …, n}. Every coordinate xi appears in this polynomial with exponents at most 1, because every bit in F2 equals its own square. This representation belongs to 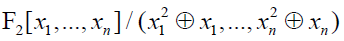 . It is called the Algebraic Normal Form (in brief the ANF). . It is called the Algebraic Normal Form (in brief the ANF). |
| Another possible representation of this same ANF uses an indexation by means of vectors of F2n instead of subsets of N; for any such vector u, we denote by au what is denoted by asupp(u) in relation (1) (where supp(u) denotes the support of u), we have the equivalent representation: |
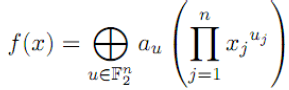 (2) (2) |
The monomial 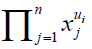 is often denoted by xu. is often denoted by xu. |
| 2.1. Relationship between a Boolean function and its ANF. |
The product 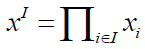 is nonzero if and only if xi is nonzero (i.e. equals 1) for every i ε I , that is, if I is included in the support of x; hence, the Boolean function is nonzero if and only if xi is nonzero (i.e. equals 1) for every i ε I , that is, if I is included in the support of x; hence, the Boolean function  takes value. takes value. |
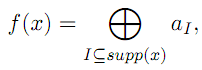 |
where supp(x) denotes the support of x. If we use the notation  we obtain the relation we obtain the relation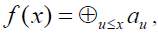 where u ≤ x means that supp(u) ⊆ supp(x) (we say that u is covered by x). A Boolean function f 0 can be associated to the ANF of f: for every where u ≤ x means that supp(u) ⊆ supp(x) (we say that u is covered by x). A Boolean function f 0 can be associated to the ANF of f: for every 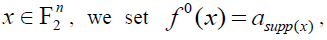 that is, with the notation that is, with the notation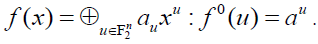 Relation (3) shows that f is the image of f 0 by the so-called binary Mobius Transform. Relation (3) shows that f is the image of f 0 by the so-called binary Mobius Transform. |
| The converse is also true: |
Proposition 1: Let f be a Boolean function on F2n and let 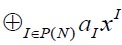 be its ANF. We have: be its ANF. We have: |
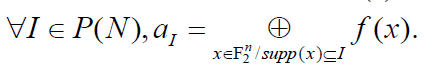 (4) (4) |
Proof. Let us denote 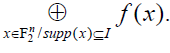 by bI and consider the function by bI and consider the function  We have We have |
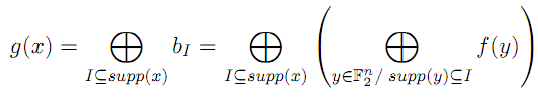 |
| and thus |
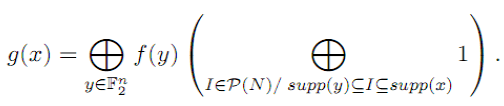 |
The sum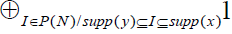 is null if y ≠ x, since the set {I ε P(N) / supp(y) ⊆ I ⊆ supp(x)} contains is null if y ≠ x, since the set {I ε P(N) / supp(y) ⊆ I ⊆ supp(x)} contains 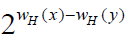 elements if supp(y) ⊆ supp(x), and none otherwise. Hence, g = f and, by uniqueness of the ANF, bI = aI for every I. elements if supp(y) ⊆ supp(x), and none otherwise. Hence, g = f and, by uniqueness of the ANF, bI = aI for every I. |
| 2.2. The degree of the ANF. |
It is denoted by d0f and is called the algebraic degree of the function (this makes sense thanks to the existence and uniqueness of the ANF): 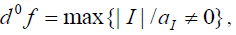 where |I| denotes the size of I. Some authors also call it the nonlinear order of f. According to Relation (4), we have: where |I| denotes the size of I. Some authors also call it the nonlinear order of f. According to Relation (4), we have: |
Proposition 2: The algebraic degree d0f of any n-variable Boolean function f equals the maximum dimension of the subspaces 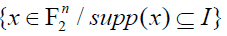 on which f takes value 1 an odd number of times. on which f takes value 1 an odd number of times. |
| The algebraic degree is an affine invariant (it is invariant under the action of the general affine group): for every affine isomorphism L: |
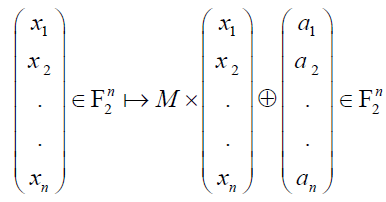 |
| (where M is a nonsingular n x n matrix over F2 ). We have d0(f o L) = d0f. Indeed, the composition by L clearly cannot increase the algebraic degree, since the coordinates of L(x) have degree 1. Hence we have d0(f o L) ≤ d0f (this inequality is more generally valid for every affine homomorphism). And applying this inequality to f o L in the place of f and to L- 1 in the place of L hows the inverse inequality. Two functions f and f o L where L is an F2 - linear automorphism of F2n (in the case a1 = a2 = … = an = 0 above) will be called linearly equivalent and two functions f and f o L, where L is an affine automorphism of F2n , will be called affinely equivalent. |
| The algebraic degree being an affine invariant, Proposition 2 implies that it also equals the maximum dimension of all the affine subspaces of F2n on which f takes value 1 an odd number of times. |
THE REPRESENTATION OVER THE REALS
|
Boolean function has proved itself to be useful for characterizing several cryptographic criteria [8, 9]. It represents Boolean functions, and more generally real-valued functions on F2n (that are called n-variable pseudo-Boolean functions) by elements of 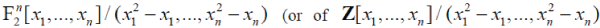 for integer-valued functions). We shall call it the Numerical Normal Form (NNF). for integer-valued functions). We shall call it the Numerical Normal Form (NNF). |
The existence of this representation for every pseudo-Boolean function is easy to show with the same arguments as for the ANFs of Boolean functions (writing 1 – xi instead of 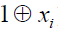 ). The linear mapping from every element of the 2n- th dimensional F2n - vectorspace ). The linear mapping from every element of the 2n- th dimensional F2n - vectorspace 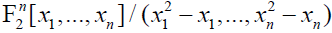 to the corresponding pseudo-Boolean function on F2n , it is therefore one to one (the F2n - vectorspace of pseudo-Boolean functions on F2n having also dimension 2n). We deduce the uniqueness of the NNF. to the corresponding pseudo-Boolean function on F2n , it is therefore one to one (the F2n - vectorspace of pseudo-Boolean functions on F2n having also dimension 2n). We deduce the uniqueness of the NNF. |
We call the degree of the NNF of a function its numerical degree. Since the ANF is the mod 2 version of the NNF, the numerical degree is always bounded below by the algebraic degree. It is shown in [4] that, if a Boolean function f has no ineffective variable (i.e. if it actually depends on each of its variables), then the numerical degree of f is greater than or equal to 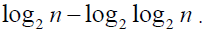 |
| The numerical degree is not an affine invariant. But the NNF leads to an affine invariant (see a proof of this fact in [8]; see also [10]) which is more discriminant than the algebraic degree: |
| Denition 1: Let f be a Boolean function on F2n We call generalized degree of f the sequence di(i≥1) defined as follows: for every i ≥ 1, di is the smallest integer di > di-1 (if i > 1) such that, for every multi-index I of size strictly greater than d, the coefficient λI of xI in the NNF of f is a multiple of 2i. |
Example: the generalized degree of any nonzero ane function is the sequence of all positive integers. Similarly as for the ANF, a (pseudo-) Boolean function 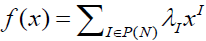 takes value: takes value: |
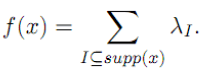 |
But, contrary to what we observed for the ANF, the reverse formula is not identical to the direct formula: Proposition 3: Let f be a pseudo-Boolean function on F2n and let its NNF be 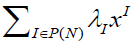 . Then: . Then: |
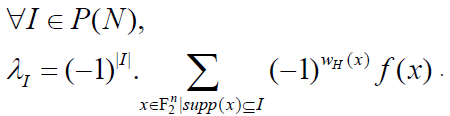 (6) (6) |
| Thus, function f and its NNF are related through the Mobius transform over integers. |
Proof. Let us denote the number 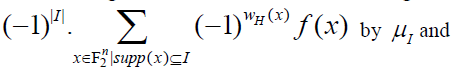 |
consider the function 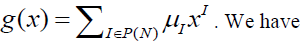 |
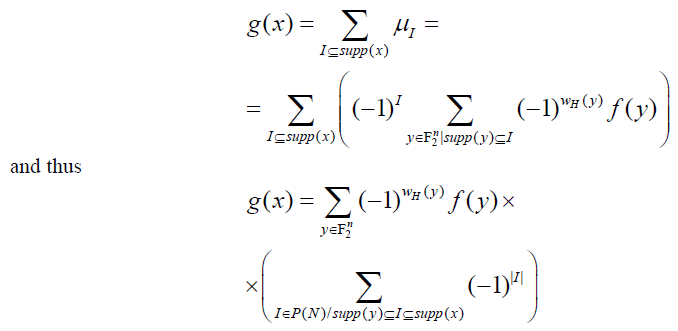 |
The sum 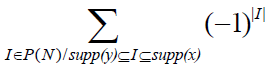 is null if supp(y) ⊆ supp(x) . It is also null if supp(y) is included in supp(x), but different. Indeed, denoting |I| - wH(y) by i, it equals is null if supp(y) ⊆ supp(x) . It is also null if supp(y) is included in supp(x), but different. Indeed, denoting |I| - wH(y) by i, it equals |
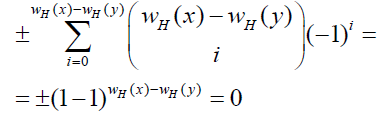 |
| Hence, g = f and, by uniqueness of the NNF, we have μI = λI for every I. |
Proposition 4: Any polynomial 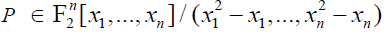 is the NNF of an integer-valued function if and only if all of its coefficients are integers. Assuming that this condition is satisffied, P is the NNF of a Boolean function if and only if: is the NNF of an integer-valued function if and only if all of its coefficients are integers. Assuming that this condition is satisffied, P is the NNF of a Boolean function if and only if: 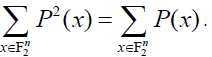 |
Proof. The first assertion is a direct consequence of relations (5) and (6). If all the coefficients of P are integers, then we have 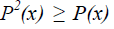 for every x; this implies that the 2n equalities, expressing that the corresponding function is Boolean, can be reduced to the single one for every x; this implies that the 2n equalities, expressing that the corresponding function is Boolean, can be reduced to the single one 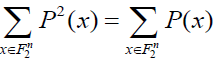 |
Let 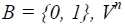 - set of vectors of length n with the coordinates of the set B. Boolean function is a mapping. - set of vectors of length n with the coordinates of the set B. Boolean function is a mapping. |
 |
| The set of all Boolean functions depending on n variables, denoted as n F . |
Monotone elementary conjunction is called the product of distinct variables without negations. The rank of a monotone elementary conjunction is the number of variables. We assume a degenerate monotone elementary conjunctions of rank 0. Every Boolean function can be written uniquely form 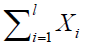 where Xi - distinct monotone elementary conjunctions, the summation is mod 2. The degree of the polynomial is the greatest rank of its terms. We say that a function f (x1, ..., xn) belongs to the class Cm, m = 0, 1, 2, ..., if it is given a polynomial of degree m. Obviously, the class C0 only contains constants 0 and 1, class C1 is the class L of linear functions. We call the derivative of f (x1, ..., xn) with respect to xi function fxi (x1, ..., xn), equal where Xi - distinct monotone elementary conjunctions, the summation is mod 2. The degree of the polynomial is the greatest rank of its terms. We say that a function f (x1, ..., xn) belongs to the class Cm, m = 0, 1, 2, ..., if it is given a polynomial of degree m. Obviously, the class C0 only contains constants 0 and 1, class C1 is the class L of linear functions. We call the derivative of f (x1, ..., xn) with respect to xi function fxi (x1, ..., xn), equal |
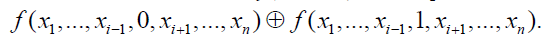 |
| Theorem 1. The function f (x1, ..., xn) belongs to the class Cm, m> 1, if and only if for each variable xi, i = 1, ... , n, function fxi (x1, ..., xn) belongs to Cm-1. |
| Proof. Follows from the definition of a derivative and a unique representation of a Boolean function by a polynomial. Let the Boolean function f (x1, ..., xn) is given a vector of its values αf on the sets listed in lexicographic order. The number of coordinates αf equal to N = 2n. |
| Theorem 2. There exists an algorithm to the vector αf with complexity O (N) determines whether the function f (x1, ..., xn) be linear, and, if so, it builds a polynomial. Proof. Consider the following algorithm. |
| i := 1; |
| fi (xi, …., xn) := f (x1, …., xn); |
| p (xi, …., xn) := f (0, …., 0). |
| Beginning of the cycle. |
| 1. Building a derivative fi xi (xi, ..., xn): divide the vector αf i in two and summarize the coordinate-wise. At the same time will be spent 2n-i+1 operations. |
| 2. if |
| • fxi (xi, ..., xn) ≡ 1, then p (x1, ..., xn): = p (xi, ..., xn) ⊕ xi; |
| • fxi (xi, ..., xn) ≡ 0, then p (x1, ..., xn) remain unchanged; |
| • Otherwise - the algorithm terminates and the answer is "nonlinear function - linearly. |
| 3. i: = i + 1, fi (xi, ..., xn) = fi-1 (0, xi, ..., xn),. To construct a vector αf i requires 2n-i+1 operations. |
| 4. if |
| • i > n, then the algorithm terminates, the answer is "linear function" and it’s written in the polynomial p (x1, ..., xn); |
| • Otherwise - go to the top of the loop. |
| The correctness of the algorithm follows from Theorem 1. |
| We calculate the complexity of the algorithm. it is |
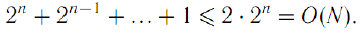 |
| Theorem 3. Given a number m> 1. There exists an algorithm for vector αf complexity O (N) determines whether an function f (x1, ..., xn) to the class Cm, and, if so, it builds a polynomial. |
| Proof. We construct the desired algorithm Am inductively. The basis of induction. Let m = 1. Then, as the algorithm A1 will consider the algorithm described in Theorem 2. Its complexity is equal to 2 . 2n. |
| Inductive step. Suppose that the algorithm Am-1 has already constructed, and its complexity is equal to Cm-1. 2n , where Cm-1 - is a constant. Consider an algorithm Am is as the following: |
| i := 1; |
| fi (xi, …., xn) := f (x1, …., xn); |
| p (xi, …., xn) := f (0, …., 0). |
| Beginning of the cycle. |
| 1. Building a derivative fi xi (xi, ..., xn): divide the vector αf i in two and summarize the coordinate-wise. At the same time will be spent 2n-i+1 operations. |
| 2. With algorithm Am-1 checks whether the function fxi (xi, ..., xn) class Cm-1. |
| if |
| • Answer "yes" and a polynomial p (x1, ..., xn), then |
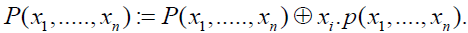 |
| • Otherwise, the algorithm terminates and the answer is "function does not belong to Cm”. |
| In Step 2, we have spent Cm-1.2n-i+1 operations. |
| 3. i: = i + 1, fi (xi, ..., xn) = fi-1 (0, xi, ..., xn). For constructing vector αf i requires 2n-i+1 operations. |
| 4. if |
| • i > n, then the algorithm terminates, the answer is "The function of class Cm” and it’s written in the polynomial P(x1, ..., xn); |
| • Otherwise - go to the top of the loop. The correctness of the algorithm follows from Theorem 1. We calculate the complexity of the algorithm. |
It is 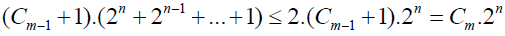 where Cm - a constant. So where Cm - a constant. So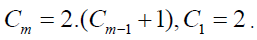 It is easy to calculate that Cm = 2.2m. Consequently, the complexity of the algorithm is (2.2m).2n = O(N), since the number m - fixed. It is easy to calculate that Cm = 2.2m. Consequently, the complexity of the algorithm is (2.2m).2n = O(N), since the number m - fixed. |
CONCLUSION
|
| In this paper we have shown that many classical notions, constructs algorithms that recognize properties of Boolean functions polynomials by their values vectors, it makes sense consider only algorithms that have lower complexity order. Linear complexity algorithm which determines the vector values a Boolean function given, it is a polynomial of fixed degree. These results are applied for the theory of cryptographic properties of Boolean functions. |
| |
References
|
- Claude Carlet, “Boolean Functions for Cryptography and Error Correcting Codes”, Lecture notes, University of Paris 8.
- Y.V. Taranikov, “On Resilient Functions with Maximum Possible Nonlinearity”, Indocrypt 2000, LNCS 1977, Springer-Verlag, pp. 19-30, 2000.
- W. Millan, A. Clark, E. Dawson, “Heuristic Design of Cryptographically Strong Balanced Boolean Functions”, Eurocrypt 98, LNCS 1403, Springer-Verlag, pp. 489-499, 1998.
- S. Maitra, P. Sarkar, “Construction of Nonlinear Boolean Functions with Important Cryptographic Properties”, Eurocrypt 2000, LNCS 1807, Springer-Verlag, pp. 485-506, 2000.
- P. Stanica, S.H. Sung, “Boolean Functions with Five Controllable Cryptogrpahic Properties, Designs, Codes and Cryptography”, Vol. 31, pp. 147-157, 2004.
- Mart De Graaf and Paul Valiant, “Polynomial representations of symmetric partial boolean functions”, Journal on Discrete Mathematics, Volume 19 Issue 2, pp. 481 – 488, 2005.
- C. Carlet, “On the coset weight divisibility and nonlinearity of resilient and correlation-immune functions”, Proceedings of SETA'01 (Sequences and their Applications 2001), Discrete Mathematics and Theoretical Computer Science, 2001.
- C. Carlet and P. Guillot, “A new representation of Boolean functions, Proceedings of AAECC'13”, Lecture Notes in Computer Science 1719, 1999.
- C. Carlet and P. Guillot. Bent, “Resilient functions and the Numerical Normal Form”. DIMACS Series in Discrete Mathematics and Theoretical Computer Science, 56, 2001.
- AnBraeken, VentzislavNikov, SvetlaNikova, and Bart Prenee, “On Boolean Functions with Generalized Cryptographic Properties”, Progress in Cryptology - INDOCRYPT 2004, Lecture Notes in Computer Science Volume 3348, pp. 120-135, 2005.
|