An Efficient Decision Tree Based Architecture for
Random Impulse Noise Removal in images

Sajan P. Philip; S. P. Prakash; Dr. S. Valarmathy

An Efficient Decision Tree Based Architecture for Random Impulse Noise Removal in images

Sajan P. Philip¹, S. P. Prakash² and Dr. S. Valarmathy³

P. G Sholar, Department of ECE, Bannari Amman Institute of Technology, Erode, India
Assistant Professor, Department of ECE, Bannari Amman Institute of Technology, Erode, India
Head of the Department, Department of ECE, Bannari Amman Institute of Technology, Erode, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Images are often degraded by impulse noise in the procedures of image acquirement and broadcast. In this paper, we propose an efficient VLSI Architecture of a Decision Tree Based Denoising algorithm which can be used for the effective removal of random-valued impulse noise in images. To accomplish the low cost, a low-complexity VLSI design is proposed. The main components of the proposed design are a Decision-Tree-Based Impulse Noise Detector to detect the noisy pixels in the corrupted image and an Edge Preserving Noise Filter to reconstruct the corrupted pixels. The Decision Tree Based Method includes a binary tree of three stages for the detection of the noisy pixel. The reconstructed pixels are written adaptively to the reconstructed image after the correction by the noise filter. The main feature of the proposed design is that it keeps the unaffected pixels untouched and thereby reducing the blurring effect in the reconstructed image. It requires only low computational complexity and two line memory buffers. The hardware cost of the proposed design is very less and therefore, the design is very appropriate to be applied to many real time scenarios.

Keywords

Noise Removal, Noise Filter, Decision Tree, VLSI Architecture, Median Filter, Impulse Noise

INTRODUCTION

In general, images are frequently corrupted by impulse noise in the events of image acquisition and broadcast. The efficiency of the Image processing techniques mainly depends on the noise in the images. Hence, a competent denoising technique becomes a very important issue in image processing [1], [2]. According to the distribution of noisy pixel values, impulse noise can be classified into two categories: Fixed-Valued impulse noise and Random-Valued impulse noise. The Fixed Values impulse noise is also known as “Salt and Pepper Noise” since the pixel value of a noisy pixel is either minimum or maximum value in grayscale images. The values of noisy pixels corrupted by randomvalued impulse noise are uniformly distributed in the range of [0, 255] for gray-scale images. Removal of Random valued impulse noise is more complicated due to the random distribution of the noise pixels. In this paper, the main focus is on the detection and correction of the random-valued impulse noise from the corrupted image.

Recently many methods have been proposed for the removal of Impulse noise from the image. They are Standard Median Filter [3], modifications of Standard Median Filter [4], [5], Switching Method [6]-[8], Alpha Trimmed Mean Based Method (ATMBM)[9], Differential Rank Impulse Detector (DRID)[10], Directional Weighted Median (DWM)[11]. The main disadvantage of the standard median method is the blurring of the reconstructed image.

The complexity of denoising algorithms depends mainly on the local window size, memory buffer, and iteration times. The lower complexity techniques use a fixed-size local window, require a few line buffers and perform no iterations. Therefore, the computational complexity is low. However, the reconstructed image quality is not good enough. Hence achieving the higher quality reconstructed image with lower complexity method is a challenge. To achieve the goal of low cost, low power, less memory and easier computations, an efficient low complexity impulse noise removal method is essential.

Based on basic concepts available in the literature, here we present an efficient decision-tree-based denoising method (DTBDM) and its VLSI architecture for detecting random-valued impulse noise. The proposed design requires simple computations and two line memory buffers only, so its hardware cost is low. The main components of the Detector part are Isolation Module, Fringe Module and Similarity Module. The main component of the Corrector part is an Edge Preserving Median Filter.

The rest of this paper is organized as follows. The proposed DTBDM Impulse Detector is introduced briefly in Section II. Section III describes the Edge Preserving Filter.Section IV discuss the VLSI Design of the above architectures. Section V describes the Results andDiscussions and Section VI concludes the results.

PROPOSED DECISION TREE BASED IMPULSE DETECTOR

Here, the window size for the denoising process is 3x3. Assume the pixel tobe denoised is located at coordinate (i, j) and denoted as pi,j,and its luminance value is fi,j. The mask under consideration is shown in Fig. 1. We have divided the other pixels in the window as Top Half and Bottom Half. The overall design architecture of the proposed method is shown in Fig 2.Several methods are employed in the literature for the impulse detection. Based on the existing designs, we have designed three modules namely, Isolation Module (IM), Fringe Module (FM), and Similarity Module (SM). Three concatenating decisions of these modules make a decision tree.

A. Isolation Module

We use Isolation Module to make a decision whether the pixel value is in a smooth region. If the result is negative,we conclude that the pixel under consideration belongs to a noisy-free area. Otherwise if the result is positive, it indicates that the pixel under consideration can be a noisy pixel or it is just situated on an edge of the object in the image. The Dataflow of the different components in Isolation Module is given in Fig. 3, Fig. 4 and Fig. 5. In order to avoid the complexity of the Design, the 3 x 3 window under consideration is divided into two different regions. Window Top Half and Window Bottom Half Where,

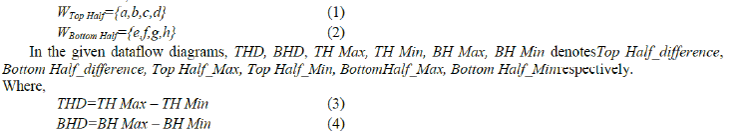B. Fringe Module

In some cases, if the pixel is situated at the edge the Isolation Module may detect it as noisy pixel, In order to deal with this scenario; we define four directions, from E1 to E4, as shown inFig. 6. By calculating theabsolute difference between fi,jand the other two pixel valuesalong the same direction, we can determine whetherthere is an edge or not. The Dataflow of the Fringe Module is given in Fig. 7 and Fig. 8.

C. Similarity Module

The last step in impulse detection is the Similarity Module. The luminance valuesin mask W positioned in a noisyfree area might be close. The medianis always positioned in the center of the variation series,whereas the impulse is frequently located near one of its ends. Hence,if there are extreme big or small values, that shows the chanceof noisy signals. Based on this perception, we sort ninevalues in ascending order and obtain the 4th, 5th and 6th valueswhich are close to the median in mask W. In order to perform the operation, we need to define the following variables.

PROPOSED EDGE PRESERVING IMAGE FILTER

Edge preservation is one of the important consideration in Denoising algorithms. The similarity of the Reconstructed image with the Original image mainly depends on the Edges in the Image. Here, we consider eight directional differences, D1-D8, for the reconstruction of the Noisy pixel in the image as shown in the Fig. The main idea adopted here is to avoid the pixels, which are already known affected, for the reconstruction of the pixel Pi,j. This is to avoid the possible misdetection of the edges. This is accomplished by using Maxi,j and Mini,j, defined in similarity module (SM), to determine whether the values of d, e, f, g and h are likely corrupted respectively. If d, e, f, g and h are all suspected to be noisy pixels, and no edge can be processed, then the estimated value of Pi,j is equal to the weighted averageof luminance values of three previously denoised pixels and calculated as (a+b x 2+c)/4. In other conditions, the edge filter calculates the directional differences of the chosen directions and locates the smallest one (Dmin) among them. The overall Dataflow of the Edge Preserving Image Filter is given in the Fig. 11.

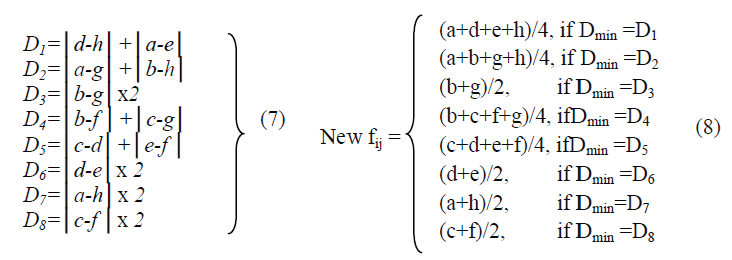VLSI IMPLEMENTATIONOF THE PROPOSED METHOD

The reduction in cost and power is achieved by reducing the complexity in the computation and using simple computation elements in the overall design. The Detector part of the algorithm is implemented using simple Comparator, Subtractor, Adder and Mux. In the Filter part, the area and cost is reduced by using shifter instead of Multiplier and Divider.

A. Design of Isolation Module

Fig. 12 and Fig. 13 shows the Hardware architecture and Implementation of the Isolation Module for the Top Half of the Window. The overall architecture will be a combination of both the Top Half and Bottom Half. The comparator CMPL is used to output the larger value from the two input values (8 bits) while the comparator CMPS is used to output the smaller value from the two input values (8 bits). The SUB unit is used to subtract two 8 bit numbers. The |SUB| unit is used to determine the absolute difference between two 8 bit umbers. The GC is the greater comparator that will output „logic 1‟ if the upper input value is greater than the lower one.Decision I is given as the selection line of the Decision II MUX.Finally, if the result of DecisionII is positive, pi,jmight be a noisy pixel or situate on anedge. The next module (FM) will be used to confirm the result.

B. Design of Fringe Module

Fig.14 shows the architecture of FM Module. The overall FM Module consists of four small structures called FM_1, FM_2, FM_3, and FM_4. Fig. 15 shows the detailed architecture of FM_1 structure. The |SUB| unit is used to calculate the absolute differences between the pixel values as given in the Dataflow of Fringe Module. The GC units will perform the comparisons and the NOR Gate will give the combined output. The combined output of each structure together selects the true or false value from the 2:1 MUX. The hardware Implementation of Fringe Module is given in Fig. 16.

C. Design of Similarity Module

Fig. 17 shows the architecture of the Similarity Module. Here the ADD and SUB units are used to calculate the Maxijand Minij. An 8 Bit 2:1 MUX is used to select the NMax and NMin. The TC unit is a Triple Comparator which will output logic 1 if the lowest input is not in between the upper values. As shown in Fig.14, we need to find out the 4th, 5th and 6th value from the sorted pixel values in the window under consideration. We have proposed a fast and efficient architecture for the sorting process. The detailed implementation of the structures is shown in Fig. 18 and Fig. 19.

The idea behind the M0 Module is as follows: If the valuea is greater thanb, C01 is set to 1; or else, C01 is set to 0. The eight GC unitsare used to determine the values from C01 to C08. After comparing,a combinational unit is used to combine the results of eachcomparator to obtain a number between 0 and 8. The number interprets the order of value in mask W under consideration. If ais the smallest valuein mask W, the output of the M0 module is 0; if a is the biggestvalue in mask W, the output is 8. The architectures of othermodules M1 to M8 are approximately the same as M0, with only littledifference. By this approach in sorting, we can find outthe order of values efficiently by using simplecomparators andcombinational units. Comparing with conventional sorting algorithms,this method speeds up the sorting time, and reducesthe space which used to store the value to be exchanged. The Hardware Implementation of SM is given in Fig.20.

D. Design of Edge Preserving Filter

The Edge Preserving Filter consists of a Minimum Edge Generator and an Average Generator. The Edge Preserving Filter is used to find out the Edge with the smallest difference. Subtracter, Adder and Shifter are the main components of the Edge Preserving Filter. There is a MinTree used in the architecture to compare and find out the smallest Edge. Now the mean of the luminance values of the pixels which has the smallest directional difference can be obtained from the average generator. If all the pixels under consideration are suspected to be noisy pixels, the final MUX will outptu (a+bx2+c)/4. Otherwise, the MUX will output the mean of the pixel values whcih has minimum Edge difference. The architecture of MinED generator and Average Generator are given in Fig.21 and Fig 22.

RESULTS AND DISCUSSIONS

The impulse detection process is a three stage process in the decision tree and it check for the smoothness of the area under consideration, position of the pixel in the edge of the image and the similarity of the pixel under consideration with the neighboring pixels. Here we have considered the Enlarged areas in the standard image “Lena”. In Fig. 23(a) a smooth area in the image is considered. In Fig. 23(c) an edge in the image is considered.Fig.23(d) is a noised added image.

In the same way the Edge preserving filter reconstruct the value by considering the neighbouring pixels. If all the neighbouring pixels are corrupted, then they will not be considered for the reconstruction of the pixel under consideration. In that case the reconstructed pixel value will be the average of the pixels a,b and c.

The architecture is designed in VHDL and synthesized in the Xilinx 14.2 Simulation Tool and the simulation results are verified. Fig. 24 (a), (b), (c) shows the simulation results of the Isolation, Fringe and Similarity Modules respectively.

Table.1 shows the comparison Line Buffer and Iteration times of different algorithms with the proposed method. The proposed design requires simple computations and two line memory buffers only. Hence its hardware cost is low, which is an important concern in Hardware Design. For a 512×512 8-bit gray-scale test image, only two line buffer (512×2×8 bits) is required in our design. Most of the promising methods need to buffer a full image (512×512×8 bits). In our design, 99.6% of storage is reduced. Moreover, only simple arithmetic operations, such as addition and subtraction, are used in our Method.

Table.2 shows the summary of the design in terms of the LUTs, Slices, and Registers etc. We can see that the design is compact and efficient due to the simple components like Adder, Subtractor, and Comparator etc are the building blocks of the Architecture.

CONCLUSIONS

A low-cost VLSI architecture for competent removal of random- valued impulse noise is proposed in this paper. The method uses the decision-tree-based detector to detect the noisy pixel in the image, and employs an effective design to locate the edge. With adaptive skill, the quality of the reconstructed images is notable improved. Our extensive experimental results demonstrate that the performance of our proposed technique is better than the previous loweromplexity methods and is comparable to the higher-complexity methods in terms It requires only low computational complexity and two line memory buffers. Therefore, it is very suitable to be applied to many real-time applications.

Tables at a glance


Table 1	Table 2

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4	Figure 5

Figure 6	Figure 7	Figure 8	Figure 9	Figure 10

Figure 11	Figure 12	Figure 13	Figure 14	Figure 15

Figure 16	Figure 17	Figure 18	Figure 19	Figure 20

Figure 21	Figure 22	Figure 23	Figure 24

References

R. C. Gonzalez and R. E. Woods, Digital Image Processing. Pearson Education, Upper Saddle River, New Jersey, 2007.

W. K. Pratt, Digital Image Processing. New York: Wiley-Interscience, 1991.

T. Nodes and N. Gallagher, “Median filters: some modifications and their properties,” IEEE Trans. ASSP, vol. ASSP-30, no. 5, pp. 739-746, Oct.1982.

S.-J. Ko and Y.-H. Lee, “Center weighted median filters and their applications to image enhancement,” IEEE Trans. Circuits Syst., vol. 38, no. 9, pp. 984- 993,Sept. 1991.

T. Sun and Y. Neuvo, “Detail-preserving median based filters in image processing,” Pattern Recognit. Lett., vol. 15, pp. 341ÃÂ¢Ãâ¬Ãâ347, Apr. 1994.

E. Abreu, M. Lightstone, S. K. Mitra, and K. Arakawa, “A new efficient approach for the removal of impulse noise from highly corruptedimages,” IEEETrans. Image Process., vol. 5, no. 6, pp. 1012ÃÂ¢Ãâ¬Ãâ1025, Jun. 1996.

T. Chen and H. R. Wu, “Adaptive impulse detection using center-weighted median filters,” IEEE Signal Process.Lett., vol. 8, no. 1, pp. 1ÃÂ¢Ãâ¬Ãâ3, Jan. 2001.

T. Chen and H. R.Wu, “Space variant median filters for the restoration of impulse noise corrupted images,” IEEE Trans. Circuits Syst. II, Analog Digit. Signal Process., vol. 48, no. 8, pp. 784ÃÂ¢Ãâ¬Ãâ789, Aug. 2001.

W. Luo, “An efficient detail-preserving approach for removing impulse noise in images,” IEEE Signal Process.Lett., vol. 13, no. 7, pp. 413-416, July 2006.

I. Aizenberg, and C. Butakoff, “Effective impulse detector based on rank-order criteria,” IEEE Signal Process. Lett., vol. 11, no. 3, pp. 363-366, Mar. 2004.

Y. Dong and S. Xu, “A new directional weighted median filter for removal of random-valued impulse noise,” IEEE Signal Process.Lett., vol. 14, no. 3, pp.193ÃÂ¢Ãâ¬Ãâ196, 2007.

.N. I. Petrovic and V. Crnojevic, “Universal impulse noise filter based on genetic programming,” IEEE Trans. Image Process., vol. 17, no. 7, pp. 1109- 1120, July 2008.

C. Y Lien, C.H Huang, P.Y Chen, Y. F Lin An Efficient Denoising Architecture forRemoval of Impulse Noise in Images, IEEE Transactions on Computers, March 2012.