Floating-point numbers are widely adopted in many applications due to their dynamic representation capabilities. Basically floating point numbers are one possible way of representing real numbers in binary format. Multiplying floating point numbers is also a critical requirement for DSP applications involving large dynamic range. The IEEE 754 standard presents two different floating point formats, Binary interchange format and Decimal interchange format. This paper presents the floating point multiplier that supports the IEEE 754 binary interchange format. This paper mainly focuses on double precision floating point multiplier based on Booth algorithm. The main object of this paper is to reduce the power consumption and to increase the speed of execution by implementing certain algorithm for multiplying two floating point numbers. In order to design this, VHDL is used and targeted on a Xilinx Virtex-5 FPGA. The implementation‟s tradeoffs are area, speed and power. In this paper Shift and Add Multiplier is compared with Radix-4 Booth Multiplier. This multiplier also handles overflow and underflow cases. For high accuracy of the results normalization is also applied.
Keywords |
| Floating point multiplier, Shift and Add Multiplier, Radix-4 Booth Algorithm, Xilinx 9.1i Synthesizer. |
INTRODUCTION |
| Floating Point (FP) multiplication is widely used in large set of scientific and signal processing computation.
Multiplication is one of the common arithmetic operations in these computations. Also the need of high speed
multiplier is increasing as the need of high speed processors are increasing. Higher throughput arithmetic operations are
important to achieve the desired performance in many real time signal and image processing applications. One of the
key arithmetic operations in such applications is multiplication and the development of fast multiplier circuit has been a
subject of interest over decades. Also reducing the time delay and power consumption are very essential requirements
for many applications. |
| Floating point numbers are one possible way of representing real numbers in binary format. The IEEE has produced a
standard to define floating point representation and arithmetic which is known as IEEE 754 standard and which is the
most common representation today for real numbers on computer. IEEE 754 basically specifies two formats for
representing floating point values. They are single precision and double precision floating point format. This paper
mainly focuses on double precision floating point multiplier. |
| In IEEE-754 double precision binary format, sign (S) is represented with one bit, exponent (E) and fraction (M or
Mantissa) are represented with eleven and fifty two bits respectively. For a number is said to be a normalized number,
it must consist of' one' in the MSB of the significand and exponent is greater than zero and smaller than 1023. The real
number is represented by equations (1) & (2). |
| Z = (-1
S
) * 2
(E -Bias) * (1. M) (1) |
| Value = (-1
Sign bit
) * 2
(Exponent -1023) * (1.Mantissa) Bias = 1023 (2) |
FLOATING POINT MULTIPLICATION ALGORITHM |
| The normalized floating point numbers have the form of Z = (-1S) * 2
(E - Bias) * (1.M) . The following algorithm is
used to multiply two floating point numbers. |
| 1. Multiplying the significand; i.e. (1.M1*1.M2) (By Using Booth Algorithm) |
| 2. Placing the decimal point in the result. |
| 3. Adding the exponents; i.e. (E1 + E2 – Bias) |
| 4. Obtaining the sign; i.e. s1 xor s2 |
| 5. Normalizing the result; i.e. obtaining 1 at the MSB of the results significand |
| 6. Rounding the result to fit in the available bits. |
| 7. Checking for underflow/overflow occurrence. |
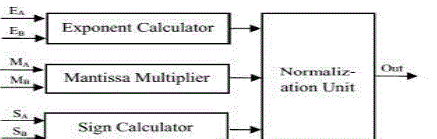
MAIN BLOCKS OF FLOATING POINT MULTIPLIER |
| A. Sign calculator |
| The main component of Sign calculator is XOR gate. If any one of the numbers is negative then result will be negative.
The result will be positive if two numbers are having same sign. |
| B. Exponent Adder |
| This sub-block adds the exponents of the two floating point numbers and the Bias (1023) is subtracted from the result
to get true result i.e. EA + EB – bias. To perform ripple carry adder (RCA) is used. The Bias is subtracted using an
array of ripple borrow subtractors. |
| C. Mantissa Multiplier Using Shift and Add Multiplier |
| Shift-and-add multiplier is the basic binary multiplier and is used commonly in all applications. Shift-addmultiplication
is the simplest way to perform multiplication. It is derived for binary n-bits x n-bits integer which can
also be used for double precision floating point number with some minor changes. Number of intermediate additions
operation for shift-and-add multiplication method is equal to number1‟s in the multiplier number. Below are the steps
for shift-and-add multiplication: |
| Step 1: Divide the multiplicand and multiplier in three fields and extract each field; those are sign, biased exponent and
fraction. |
| Step 2: Sign of resultant multiplication will be XOR of the sign bits of the multiplier and the multiplicand. |
| Step 3: Biased exponent of the resultant will be addition of the biased exponents of the multiplier and the multiplicand
and subtracting the bias (i.e. 1023 for double precision). |
| Step 4: Starting from the LSB of the multiplier, add the multiplicand if there is „1‟ at the LSB of the multiplier, then
shift multiplier 1 place to the right. |
| Step 5: Repeat step 4, until all the fraction bits from multiplier are considered shifting multiplicand to the right per
every bit of multiplier, including the leading „1‟ of the normalized floating point number. |
| Step 6: Normalize the final number if necessary, shifting it right and incrementing the biased exponent. |
| D. Mantissa Multiplier Using Radix-4 Booth Algorithm (Proposed Work) |
| Multiplication involves two basic operations i.e. the generation of partial products and their accumulation. Therefore
there are two possible ways to speed up multiplication i.e. reduce the number of partial products or accelerate their
accumulation. A smaller number of partial products reduces the complexity; and as a result reduces the time needed to
accumulate the partial products. Therefore Booth algorithm is used to Speed up the Multiplication. |
| Booth algorithm provides a procedure for multiplying binary integers in signed-2‟s complement representation. Radix-
4 booth encoder performs the process of encoding the multiplicand, based on multiplier bits. It will compare 3 bits at a
time with overlapping technique. By using this technique, partial products are reduced by half. Grouping starts from the
LSB & the first block only uses two bits of the multiplier & assumes the zero for the third bit. For Example |
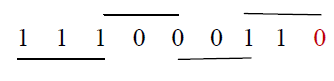 |
| Booth algorithm which scans strings of three bits is given above. Append a 0 to the right of the LSB of the multiplier.
According to the value of each vector, each Partial Product will be 0, +M, -M, +2M or -2M. |
| Booth Multiplier provides: |
| • Ease in multiplication |
| • Greater speed. |
| • Low power consumption. |
| • Less delay. |
| E . Normalizer |
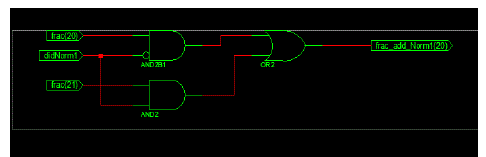
| The result of the significand multiplication (intermediate product) must be normalized to have a leading „1‟ just to the
left of the decimal point. The shift operation is done using combinational shift logic made by multiplexers. |
UNDERFLOW/OVERFLOW DETECTION |
| Underflow/Overflow means that the result‟s exponent is too small/large to be represented in the exponent field. An
overflow may occur while adding the two exponents or during normalization. Overflow due to exponent addition may
be compensated during subtraction of the bias; resulting in a normal output value (normal operation). An underflow
may occur while subtracting the bias to form the intermediate exponent. If the intermediate exponent < 0 then it‟s an
underflow that can never be compensated; if the intermediate exponent = 0 then it‟s an underflow that may be
compensated during normalization by adding 1 to it. |
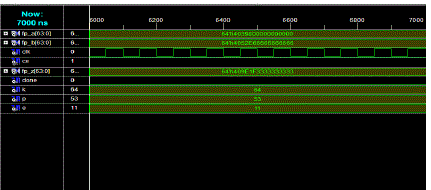
SIMULATION AND RESULT |
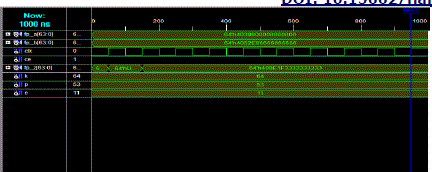
| The simulation results for corresponding inputs are shown in Fig. The simulation is done using Xilinx 9.1i.
Considering the random 64 bit floating point numbers, |
| INPUT: a = 25.5 |
| b = 75.6 |
| OUTPUT:
25.5* 75.6= 1927.8 |
 |
CONCLUSION |
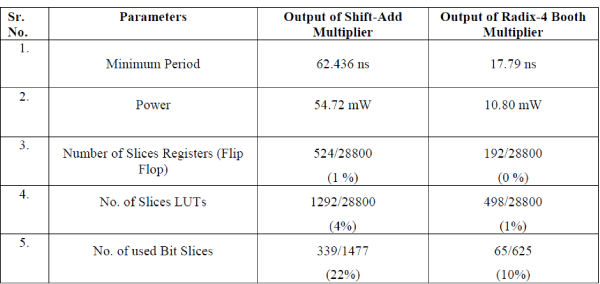
| This paper presents an implementation of Double precision floating point multiplier which shows the comparison
between Shift-Add and Radix-4 Booth Algorithm. The Multiplier has been designed on Xilinx, Virtex-5, FPGA. The
multiplier is more precise because it doesn‟t implement rounding and just presents the significand multiplication. As
compared to Shift-Add Multiplier, Radix-4 Booth Multiplier gives high speed, less delay, utilize less area and consume
low power. |
Tables at a glance |
 |
 |
| Table 1 |
Table 2 |
|
| |
Figures at a glance |
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
 |
 |
 |
 |
 |
| Figure 6 |
Figure 7 |
Figure 8 |
Figure 9 |
Figure 10 |
|
| |
References |
- IEEE 754-2008, IEEE Standard for Floating-Point Arithmetic, 2008.
- Mohamed Al-Ashrfy, Ashraf Salem and WagdyAnis “An Efficient implementation of Floating Point Multiplier” IEEE Transaction on VLSI
- B. Fagin and C. Renard, “Field Programmable Gate Arrays and Floating Point Arithmetic,” IEEE Transactions on VLSI, vol. 2, no. 3, pp. 365- 367, 1994.
- L. Louca, T. A. Cook, and W. H. Johnson, “Implementation of IEEE Single Precision Floating Point Addition and Multiplication on FPGAs,”Proceedings of 83 the IEEE Symposium on FPGAs for Custom Computing Machines (FCCM‟96), pp. 107-116, 1996.
- N. Shirazi, A. Walters, and P. Athanas, “Quantitative Analysis of Floating Point Arithmetic on FPGA Based Custom Computing Machines,”Proceedings of the IEEE Symposium on FPGAs for Custom Computing Machines (FCCM‟95), pp.155-162, 1995.
- Jaenicke and W. Luk, "Parameterized Floating-Point Arithmetic on FPGAs", Proc. of IEEE ICASSP, 2001, vol. 2, pp.897-900.
- [7] Sixth Asilomar Conference on Signals, Systems, and Computers, 2002.
- “DesignChecker User Guide”, HDL Designer Series 2010.2a, Mentor Graphics, 2010.
- “Precision® Synthesis User‟s Manual”, Precision RTL plus 2010a update 2, Mentor Graphics, 2010.
- Patterson, D. & Hennessy, J. (2005), Computer Organization and Design: The Hardware/software Interface , Morgan Kaufmann .
|