Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

An Efficient Index for Ranking in Spatial Data base

S.Krishnaveni, K.Sangeetha
Assistant Professor, Dept. Of CSE, Apollo Engineering College, Chennai, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In reality spatial objects (e.g., Dams) not only have spatial locations but also have quality attributes (e.g., height, reservoir capacity).Given a spatial location S, Quality vector ψ and a set of spatial objects D, a spatial query which retrieves and ranks the objects that intersect the region S and satisfies the quality vector. Based on the inverted index and the linear quad tree, we propose a novel index structure, called inverted linear quad tree (IL-Quad tree), which is carefully designed to exploit both spatial and keyword based pruning techniques to effectively reduce the search space which performs 1) spatial filtering ,2) textual filtering and 3) object ranking in a fully integrated manner. The inverted quad tree is compared with the R tree, SKR tree.

Keywords
IL- quadtree,R-tree, SKR-tree ,Query Processing, Spatial database.

INTRODUCTION
Spatial database systems manage large collections of geographic entities, which apart from spatial attributes contain non spatial information. Spatial objects in reality are associated with multiple quality attributes in addition to their spatial locations. Traditional spatial queries and joins focus on manipulating only spatial locations and distances, but they ignore the importance of quality attributes. The dominance comparison is suitable for comparing two objects with respect to multiple quality attributes. For the sake of simplicity, we assume that the domain of each quality attribute is fully ordered (e.g., integer domain). An object A is said to dominate another object B, if A is no worse than B for all quality attributes and A is better than B for at least one quality attribute. In this system, we study an interesting type of spatial queries, which select the best spatial location with respect to the quality of facilities in its spatial neighbourhood. Given a set D of interesting objects (e.g., candidate locations) and quality vector, a top-k spa tial preference queries retrieves the k objects in D with the highest scores. The score of an object is defined by the quality of features (e.g., facilities or services) in its spatial neighbourhood. As a motivating example, consider a database containing all information of dams. Here “feature” refers to specific facilities or services. A customer may want to rank the contents of this database with respect to the quality of their locations, quantified by aggregating non spatial characteristics of other features (e.g., height of dam, reservoir capacity etc.,) .
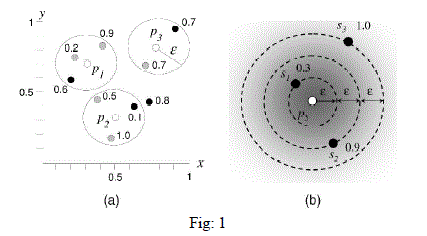
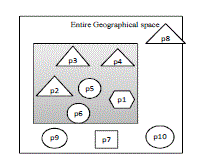
In Fig.1a, a simple score instance, called the range score, binds the neighborhood region to a circular region at p with radius (shown as a circle), and the aggregate function to SUM. For example, the maximum quality of p1(dam1) are 0.9 and 0.6. Hence the τ(p1) is 0.9+0.6=1.5.Similarly for the dam p2, τ(p2) is 1.0+0.1=1.1.Hence the dam p1 is returned as top result. Fig.1b shows a dam p5 and three features s1, s2, s3 (with their quality values). The circles have their radii as multiples of τ Now, the score of si is computed by multiplying its quality with the weight 2^-j, where j is the order of the smallest circle containing si.[1]
Traditionally, there are two basic ways for ranking objects: 1) spatial ranking, which orders the objects according to their distance from a reference point, and 2) non spatial ranking, which orders the objects by an aggregate function on their non spatial values. The top-k spatial preference query integrates these two types of ranking in an intuitive way.

PROBLEM STATEMENT
Let c be the number of (numeric) quality attributes.Each object p in the object dataset D is composed of a set of quality attributes c, and is associated with a location Lp. A quality vector is a point ψ in the cdimensional space where each dimension refers to a quality attribute. As a shorthand notation, we use ψ[i] to represent the ith (quality) attribute value of ψ. The notion of dominance is used to compare quality vectors. A quality vector ψ is said to dominate another one ψ’ (denoted as ψ<ψ’), if ∃1 ≤ i ≤ c, ψ[i] is better than ψ’[i] and ∀1 ≤ i ≤ c,is not worse than ψ’[i].
A location is a pair (x, y) in the Euclidean space, where x and y are the coordinates values. A spatial object p=<loc,ψ> consists of both a location o.loc and a quality vector o.ψ. The notation dist (p, p’) denotes the Euclidean distance between the locations of the spatial objects p and p’. Given two spatial objects p and p’ is said to be a dominator of p’ when p.ψ<p’.ψ. Given a query q that specifies a set of query keywords Wq a query spatial scope Sq, textual relevance and spatial relevance of object p to q are formalized in definitions 1 and 2, respectively.
Definition 1 (Textual relevance). An object p is said to be textually relevant to a query if o contains queried keywords i.e., Wp∩Wq≠0. To quantify the relevance of p to q, a weighting function denoted by τq(o) is adopted. Thus for a given q, τq(p1) > τq(p2) means object p1 is more textually relevant to q than object p2.
Definition 2( Spatial relevance). An object o is said to spatially relevant to a query q if the location of object o overlays with the query spatial scope of q, i.e., Lp∩Sq≠0. Let τq(o) be a scoring function to quantify the spatial relevance of o to q. Thus for a given q, τq(p1) > τq(p2) means object p1 is more spatially relevant to q than object p2.
Accordingly, k objects are retrieved from D objects that are both textually and spatially relevant to a given query and ranks objects based on the quality features of their objects.
The spatial relevance of an object p, denoted as τ(p) depends on the types of the spatial relationships defined between an object location Lq. and a spatial scope S. Commonly adopted relationships include
1. Enclosed. τ(p) is set to 1 if the corresponding location is fully enclosed by the query scope, i.e.,
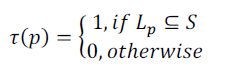image
2. Overlapping. τ(p) is set to the fraction of the object location that is covered by the spatial scope,.
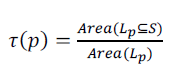image
3. Proximity. τ(p) is represented by the inverse of the distance between the center of Lp and that of S,i.e.,
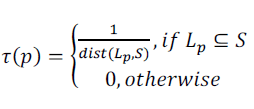image
Definition 3 ( Nearest dominator, Nearest Dominator Distance). Given a location S .its quality vector ψ, and a set of spatial objects D, the nearest dominator of S in D is defined as
ND(S,ψ,D)= argmin dist(S,p)
pεD,p.τ<ψ
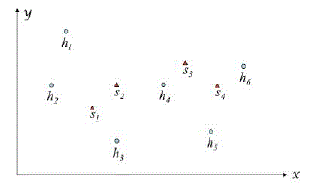
i.e., the nearest neighbor of S in D among those that dominate ψ. The nearest dominator distance ndd(S,ψ,D)=dist(S,ND(S,ψ,D)). Refer to the example in Fig 2 and 3, the ND of S is the dam hj that minimizes the dist(Sj,hj) value, among those dams dominating the design competence ψ.In Fig 2.b. lists the NN and ND of each location Sj. It is important to note that NN is not necessarily the same as ND. For example, the NN of S2 is h4 which, however, does not dominate S2 with respect to its design competence. Whereas its next nearest neighbour h3 does, which exactly is S2’s ND. By considering the distance of each location Sj from its ND, we pick the largest one(i.e., dist(S3,h5)), and take its location(i.e., S3) as the result location for building the new dam.

Definition 4 (Farthest Dominated Location Query)
Given a set of (competitors’) spatial objects D, a set of (candidate)locations L, and a quality vector ψ as the design competence, the farthest dominated location query returns from L a location S such that the distance ndd(S,ψ,D) is maximized, i.e.,
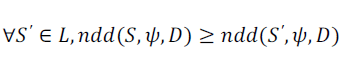image

SPATIAL QUERY EVALUATION ON R TREE
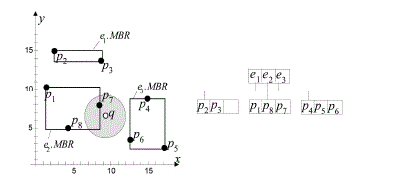
The most popular spatial access method is the R-tree [3], which indexes minimum bounding rectangles(MBRs) of objects. Fig.4 shows a set D{p1,p2..p8} of spatial objects (e.g., points) and an R-tree that indexes them. R-trees can efficiently process main spatial query types, including spatial range queries, nearest neighbour queries, and spatial joins. Given a spatial region S, a spatial range query retrieves from D the objects that t intersect,
For instance, consider a range query that asks for all objects within the shaded area in Fig.4 Starting from the root of the tree, the query is processed by recursively following entries, having MBRs that intersect the query region.For instance, e1 does not intersect the query region, thus the sub tree pointed by e1 cannot contain any query result. In contrast, e2 is followed by the algorithm and the points in the corresponding node are examined recursively to find the query result p7. The upper bound score of an object is calculated using the formula
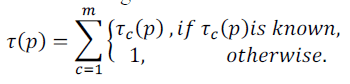image

SPATIAL QUERY EVALUATION ON SKR TREE
In Fig. 5.assume if a user Alice in Boston issues a geographic Query “Boston’s pollution control irrigation ” and the top-3 dams are to be returned. In this query, “pollution control” and “irrigation” are query keywords, and “Boston” represents a location/area of her interest. Regardless of the order of their relevance, this example shows a set of candidate objects {p2, p3, p4, p5 p6}, with respect to both textual relevance and spatial relevance. Here, p1, although being within “Boston,” is not relevant because it contains neither “pollution control” nor “irrigation.” On the other hand, {p7, p8, p9, and p10} although being textually relevant to the query, are not within “Boston.” The top-3 dams in the candidate set that are most relevant are returned.
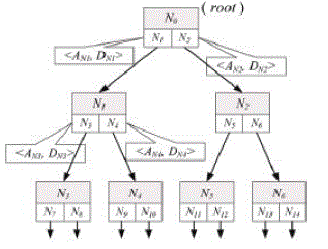
For this we proposed an efficient indexing scheme called SKR tree which indexes both the textual and spatial contents of objects to support data retrievals based on their combined textual and spatial relevance’s, which, in turn, can be adjusted with different relative weights. Fig.6. Shows the structure of SKR tree where each node has both spatial and non spatial information of the data object. No is the Root node which has two child nodes N1 and N2. The child node has the keyword AN1, and spatial data DN1 .This indexing scheme performs textual filtering and spatial filtering and hence it is efficient when compared with the R tree indexing scheme.

SPATIAL QUERY EVALUATION ON IL-QUAD TREE
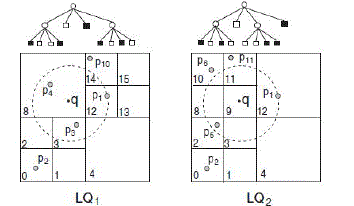
IL-Quadtree. In the paper, for each keyword ti ∈ V we build a linear quadtree, denoted by LQi, for the objects which contain the keyword ti. Besides the black leaf nodes, we also explicitly keep the quadtree structure, which serves as the signature of the objects in LQi, which can be easily fit into the main memory. More specifically, a bit is kept for each node of the quadtree, which is set to 1 for black leaf nodes and non-leaf nodes and 0 otherwise.
Obviously, a node in LQi is empty (i.e., it does not contain any object with keyword ti) if the bit is set to 0 Fig. 7 illustrates the linear quadtrees LQ1 and LQ2 constructed for keywords t1 and t2 respectively.
Index Maintenance. For an incoming new object o, it will be inserted into the corresponding linear quadtrees based on its textual information. Particularly, a leaf node of the quadtree is split if it contains more than c objects and it does not reach the maximal depth w which is the pre-determined maximal partition level. As to the deletion, an object o will be removed from its corresponding linear quadtrees. Meanwhile, some of the cells may be merged due to the deletion. For the effectiveness of the signatures, we enforce that all objects are pushed to the black leaf node below the level w_ (minimal partition level) because a black leaf node at high level may impair the pruning capability.

ALGORITHMS FOR SPATIAL PREFERENCE QUERY

A. Range Score Algorithm
Given a set of objects, the range score algorithm calculates the Nearest neighbour distance and ranks the objects.[4].
Input: A set of data D, query location , Root of R tree and the radius ε .
Output: Top k data with shortest distance
Procedure:
1: Group_Range(Node N )
2: for each entry e N do
3: If N is nonleaf then
4: read the child node N I pointed by e;
5: Group_Range(N I );
6: else
7: for each p εV such that dist (p, e) ≤ ε then
8: update Wk by e;
B. Branch and Bound Algorithm
Branch and bound algorithm which calculates the score and ranks the objects based on the non spatial quality features of the objects.
Input: A set of data D and Query location and root of R tree
Output: Top k data with the highest score.
Procedure:
1: Cal_Score(Node N )
2: for each entry e ε N do
3: If N is nonleaf then
4: read the child node N I pointed by e;
5: Cal_Score(N I );
6: else
7: for each p ε V such that
8: for c:= 1 to m do
9: compute Tc(e) for all e ∈ V concurrently;
10: update Wk by e
C. SKR Tree Construction Algorithm
Input: Set of Objects D
Output: Root of SKR tree
Procedure:
image
D. SPATIAL KEYWORD RANKING algorithm
image
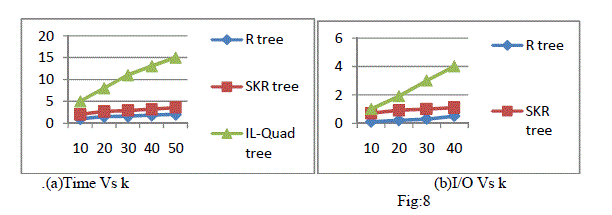
In this section, we conduct experiments on real object and feature data sets in order to demonstrate the application of top-k spatial preference queries. We obtained real spatial data from http://www.fao.org/nr/water/aquastat/gis/index2.stm location in these data sets correspond to (longitude and latitude) coordinates in Africa and Middle East countries.
This Spatial dataset containing information about dams in South Africa and middle east countries which has several features like irrigation, water supply, flood control, Hydro electricity, navigation , recreation, pollution control, livestock rearing and others. We used SQL server 2008 for spatial database design. Spatial query visualiser to visualize the spatial query and spatial up loader to upload the shape files of Africa and Middle East countries. The proposed indexing scheme is evaluated with the R tree and SKR tree

CONCLUSION
In this paper, we studied top-k spatial preference queries, which provide a novel type of ranking for spatial objects based on qualities of features in their neighbourhood. Given a spatial location S, Quality vector ψ and a set of spatial objects D, a spatial query which retrieves and ranks the objects that intersect the region S and satisfies the quality vector. We proposed an efficient index called IL-Quad tree and algorithms which performs 1) spatial filtering, 2) textual filtering and 3) object ranking in a fully integrated manner.
In the future, we will study the top-k spatial preference query on a road network, in which the distance between two points is defined by their shortest path distance rather than their euclidean distance. The challenge is to develop alternative methods for computing the upper bound scores for a group of points on a road network.

Tables at a glance
Table icon
Table 1
 

Figures at a glance


Figure Figure Figure Figure
Figure 1 Figure 2 Figure 3 Figure 4
Figure Figure Figure Figure
Figure 5 Figure 6 Figure 7 Figure 8
 

References