Research and Reviews - International Journals

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

An Efficient Numerical Methods for the Prediction of Clusters using K-means Algorithm with Bisection method for Comparing Uniform and Random Distribution Data Points

D.Napoleon1, M.Praneesh2
  1. Assistant Professor, Department of Computer Science, Bharathiar University, Tamilnadu, India
  2. Assistant Professor, Department of Computer Science, Sankara College of Science and Commerce, Tamilnadu India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

In this paper we extract the cluster by using numerical as well as statistical methods for improving efficiency using efficient algorithms of k-means in data mining. So, Data mining is defined as finding hidden information in a database it has been called exploratory data analysis, data driven discovery, and deductive learning.[1] clustering is usually accomplished by determining the similarity among the data on predefined attributes. The most similar data are grouped into clusters. This paper proposes a method for making the k-means algorithm and Bisection method for more effective and efficient, so as to getting better cluster.

Keywords
Data Clustering, K-means, Cluster analysis, Bisection methods.

INTRODUCTION
Data mining involves the use sophisticated data analysis tools for discover previously unknown, valid pattern and relationships in large datasets. Here clustering is alternatively referred to as unsupervised learning or segmentation. It can be thought of as partitioning or segmenting the data into groups that might or might not be disjointed. [1, 3] A cluster is a collection of objects which are similar between them. Clustering does not have any predefined class. The main advantage of clustering is that interesting patterns and structures can be found directly from very large data sets with little or none of back ground knowledge. The k-means algorithm is successful in producing cluster for many practical applications such as plant and animal classification, image processing, pattern recognition, and document retrieval. But the complexity of the k-means algorithm is very high, especially for large data sets. Moreover, the k-mean algorithm results in different types of clusters on the random choice of initial centroids. [3] So over come of this problem many researchers for improving the performance of k-means algorithms. Here the cluster are formed according to the distance between data points and cluster centers are formed for each cluster for this implementation plan will be in random of input data points. The implementation work was used in mat lab programming software. The number of cluster is chosen by user. Finally cluster is displayed by different colors.

II. PREVIOUS WORK
Normally, the computer must able retrieve data from a database without any human assumption on specific domain. One of the main task for the system is similarity comparison, extracting feature signatures of every data based on its input values and defining rules of comparing the data’s. So previously the Newton method is assigned for evaluating the cluster using uniform data points. So this process is not effective to handling large datasets. [2, 7] So in order to overcome the previous method limitations, now we apply the bisection method for handling the large dataset with random data inputs

III. PROPOSED WORK
A system developed for classifying a cluster using adult datasets (fig-3). Here the three main tasks of the system are
A. K-means clustering.
B. Bisection method.
C. Similarity matching.
A. K-MEANS CLUSTERING
K-means is an iterative clustering algorithm in which items are moved among sets of clusters until the desired set is reached. A cluster is a collection of data objects that similar to one another with in the same cluster and is dissimilar to the objects in the other clusters. It is the best suited for data mining because of its efficiency in processing large datasets. [1, 5] The cluster mean of
Ki = {ti1,ti2,……………….,tim} is defined as
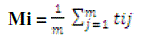image

Algorithm 3.1.The k-means clustering algorithm

Input:
D = {d1, d2,......,dn} //set of n data items.
k // Number of desired clusters

Output:
A set of k clusters.
1. Arbitrarily choose k data-items from D as initial centroids;
2. Repeat Assign each item di to the cluster which has the closest centroid;
Calculate new mean for each cluster;
Until convergence criteria is met.
As a result of this loop, the k- centroids may change their position in step-by-step manner. The k-means procedure is easily programmed and is computationally, economical, so that is feasible to process very large samples on a digital computer. The advantage of k-means algorithm is that it works well when cluster are not well separated from each other, which is frequently encountered in data’s. However, the k-means requires the user to specify the initial cluster centers.

B. BISECTION METHOD
Bisection method at the same time gives a Proof of the intermediate value theorem and provides a practical method to find the cluster of the corresponding intervals. Here basically we are allocating the intervals in [1 to 15] for estimating the user requirements [15, 16]. Let f(x) be the continuous function on the intervals [a, b]. let assume that f(a) < 0, while f(b) > 0 , the other case being handled similarly, set a0=a, b0=b. now consider the midpoint m0 = 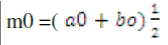image for here our data is segmenting the initial node to end node. For classifying the data, we are following the basic properties.
1. (a0) is increasing sequence; (bn) is a decreasing sequence.
2. an ≤ bn for all n.
3. f (an) < 0 for all n, f(bn) > 0 for all n.
4. bn-an = (b –a) for all n.
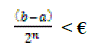It follows from the first properties that the sequence,(an) and (bn) coverage; set image andimage The third property and the continuity of the function f(x) imply that f (a) ≤ 0 and that f (b) ≥ 0. The crucial observation is the fact that the fourth properties implies that a = b. consequently. F (a) = f(b) = 0. When we enter the loop f (a) and f (b) have a opposite sign. It follows that either f (m) or f (a) have an opposite sign. Thus the initial conditions are still satisfied each time we enter the loop. [20, 23] The length of initial condition interval is (b – a). After one time through the loop the length is (b – a) / 2, after two times it is (b- a) /4, after n passes through the loop, the length of the remaining interval is (b – a) /2^n. No matter how small €, eventually (b – a) / 2^n < €. In the fact we can solve this inequality for n
image
Check the loop with in n times, whether the cluster in behind the centre or not, for checking we are use below inequality condition.
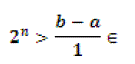image
After Checking in equality condition we are calculate the Length the attributes in below condition
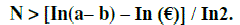image
Finally we are check the nearer attributes in the root of the equation.
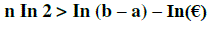image
For this equation compute the classified data in data mining. Compare the speed of convergence the Newton method can be unreliable. If algorithms encounters a point x where f ‘(x) = 0, it crashes; if it encounters point where the derivative is very close to 0 it will become unreliable. The bisection method on the other hand will always work, once you have found starting points a and b where the takes opposite signs and classifying the given data sets. For the below figure- 4 represents bracket technique for using entering the attributes of data clustering [23]. The main usage of bracket rule in applying data mining is to obtaining the data attributes to extract the cluster.

Bracket rule algorithm.
1. f(a) f(b) < 0
2. c = 0.5 (a + b)
3. check f(a) f(c) < 0:
% if not then f(c) f (b) < 0
Repeat. This algorithm examines the no of attributes of clustering.

Bisection algorithm:
The steps to apply the bisection method to find the intervals of the equation as well as find attributes of data cluster.
1. Choose xl and xu as two guesses for the root such that f ( xl) f (xu) <0, or in the other words, f(x) changes sign between xl and xu.
2. Estimate the root, xm, of the equation f(x) = 0 as the midpoint between xl and xu as xm = xl +xu/2.
3. Now check the following
a) f(xl) f(xm) < 0 then the root lies between xl and xm; then xl = xl and xu = xm.
b) f(xl) f(xm) > 0 then the roots lies between xm and xu; then xl= xm and xu = xu.
c) If f(xl) f(xm) = 0; then the root is xm. stop the algorithm if this is true.
4. Find the new estimate of the root xm = xl + xm / 2.
Find the absolute relative approximate error as finding the present iteration and previous iteration calculation process.
| ? | = xm (new) – xm (old)/ xm(new) * 100.
5. Compare the absolute relative approximate error | ? | with the pre-specified relative error tolerance ?s. if | ?a | > ?then go to step 3, else stop the algorithm.
Note one should also check whether the number of iterations is more than the maximum of iterations allowed. If so, one needs to terminate the algorithm and notify the user about it.

C. SIMILARITY MATCHING
Euclidean distance is used for similarity matching in the present system. The Euclidean distance between two points p = ( p1, p2,…pn) And Q = (q1, q2,...qn), in Euclidean space, is defined as:
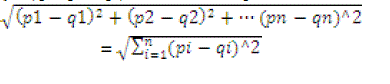image
System calculates the Euclidean distance of data of given query data to all other data in the data base. As with classification, then we measure the similarity distance or measure, sim (ti, tl) defined by two tuples, ti, tl € D. Some of the clustering algorithm looks only at numeric data, usually assuming metric data points. But Euclidean distance handle both numeric data and image data in a given data base.

IV. RESULTS AND DISCUSSION
For this paper we are taken an adult dataset to computing the various techniques like clustering and bisection methods for predicating the cluster. The resulting cluster of random data points of k – means algorithm is presented in fig -1, 2.
The random data points can be taken to easily implement and take the results of convenient for our data sets. Data points are given by the user during the execution of the program. For different input data points, the algorithm gives different outputs.

V. CONCLUSION
In this research, the random data points are used easily implement the values and get good results. For main purpose of using this research is privacy and security for data clustering. For this paper the future work is to calculate suppression for corresponding data sets. So at last the effective k- means and bisection for numerical methods is very efficient to classify the cluster in large data sets.

Figures at a glance
Figure 1 Figure 2 Figure 3
Figure 1 Figure 2 Figure 3
 

References