International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

An Experimental Implementation of Convolution Encoder and Viterbi Decoder by FPGA Emulation

Shraddha Shukla1, Nagendra Sah2
  1. PG Student [VLSI], Dept. of E&EC, PEC University of Technology, Chandigarh, India
  2. Assistant professor, Dept. of E&EC, PEC University of Technology, Chandigarh, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

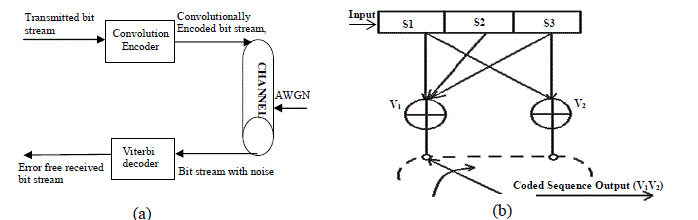
Error-correcting convolution codes prove to be a powerful methodology to limit the effects of noise in digital data transmission. Convolution Encoding with Viterbi decoding is a powerful Forward Error Control (FEC) technique that is a proven mechanism in which the transmitted signal remains uncorrupted mainly by Additive white Gaussian Noise residing inside a channel. In this work, a Convolution Encoder and Viterbi Decoder with a constraint length of 3 and code rate of ½ have been developed on xc3s250e-4-pq208 Spartan 3E board. VHDL language is used as a design entry. It is simulated and synthesized using Modelsim 6.4a and Xilinx 8.1i ISE respectively. With this way of configuration, the FPGA is capable of operating by itself as a Convolutional encoder or Viterbi decoder. Hence, it gains benefit through the reuse of the same hardware

Keywords
Convolution Encoder, Viterbi Decoder, Trellis Diagram, FPGA, VHDL, Spartan 3E development board, Additive White Gaussian Noise (AWGN).

INTRODUCTION
An error free communication system can be realized efficiently by adding appropriate redundancy at the source end to enhance error resilience of the coded bit streams [1]. The code can be recovered significantly even in the presence of noise.
The error can be detected and/or corrected by the help of dedicated hardware and software. The errori detection/correction capability can be further grouped in the following ways:
1. Automatic Repeat Request (ARQ) in which message is retransmitted whenever error is detected,
2. Forward Error Control (FEC) in which errors are corrected automatically on its occurrences, and
3. ARQ- FEC Hybrid.
Block codes and Convolution code are the popular error coding schemes most often used [2][3].
Convolution codes were first introduced in1955 by Elias as FEC coding scheme [4]. This finds its place in many applications because it was very effective in combating presence of Additive White Gaussian Noise (AWGN). Hence before transmitting the message through a noisy channel it is first convoluted by doing so the data capacity of channel increases significantly [5].
A Viterbi decoder was developed by Andrew Viterbi in 1967 to decode convolutionally encoded messages [3]. The algorithm back-tracks state sequences the encoder is most likely to have gone through. This information is used to determine the original message.
The mechanism of these encoders and decoders are described in the next section.

BACKGROUND THEORY
In block coding scheme, message estimation is based on each individual sample in the signal whereas the convolution encoding process encodes a message depending on previous data bit sequence. In this way a level of correlation between each sample in the signal is automatically obtained. Convolution coding scheme can be applied to both continuously running data stream as well as to blocks of data, whereas block codes are suited only for the latter. Convolution encoding scheme can be devised for correcting random error, burst errors or both [6]. The combination of Convolution Encoder along with Viterbi decoder is a very powerful FEC technique. It is simple and has good performance with low implementation cost [7].

A. Convolution Encoder
Convolution encoding is an error control coding technique used to encode bits before transmission over a noisy channel. They are widely used in modems and digital cellular telephony. In comparison to block encoding, Convolutional encoding is an attractive encoding scheme due to its low latency. A convolutional encoder is implemented as a Mealy machine whose output is a function of the present state and the input applied.
As illustrated in Figure. 2, a typical convolution encoder comprises of an N-stage shift register and ν modulo-2 adders. All the modulo-2 adders can be implemented using XOR gates. A convolution encoder is characterized in (N, k, v) format. Here, v represents the number of outputs of the encoder; k is the number of inputs of the encoder, N-1 is the number of memory elements (Flip- Flops) and N represents the constraint length. The rate of encoder is given by k/v. The source data sequence, input(n) = (input(0), input(1), input(2),…….), is entered into N stage shift register of encoder, one bit at a time. The resulting output sequences, V1, V2 are generated by modulo 2 adders corresponding to each entering inut. The constraint length plays an important role in the efficiency of convolution encoder hence, it needs a better understanding.
Constraint Length: Constraint length is the number of memory elements used in the shift register, to add redundant bits along with the arriving single bit input. For a constraint length of 3, the possible state transition and outputs have been calculated and tabulated in Table 1.
The hardware resource requirement hugely changes in response to channel noise conditions. Based on noise level at a specific instant of time, minimally sufficient hardware resources are allocated to meet the BER requirements of the application while achieving maximum performance. In case of a significantly noisy channel, a large constraint length such as K = 14, is demanded, to achieve a BER similar to that achieved by a constraint length K = 3 for a less noisy channel [8].
Convolution Decoding: By the use of differential detection technique and with the aid of a matched filter at the receiver one can easily retrieve the transmitted symbols by means of a decision-feedback equalization (DFE) or maximum-likelihood sequence estimation (MLSE) using the Viterbi algorithm [9].To decode a convolution code some algorithm must be adopted at the receiver side. Few categories of algorithms that already exist for such purpose are listed below:
Threshold decoding: It is the simplest and one of the earliest to be developed of them. It proves to be efficient and successful for only a specific class of convolution codes. However, it is not an optimal choice [10].
Sequential decoding: Such algorithms perform much better than threshold algorithms. Its benefit lies in the fact that its decoding complexity is virtually not governed by the length of the particular code. Even though their results are suboptimal, but they are used to decode very long codes, wherever it becomes difficult to apply any other algorithm. The main disadvantage of sequential decoding is its unpredictable latency that may occur in the decoding process [11].
Viterbi decoding: In maximum likelihood sense this is the most optimal algorithm for decoding of a convolution code. However it becomes severely difficult to decode via Viterbi decoding as the complexity increases. Hence, it can be employed only for relatively short codes. [12]

B. Viterbi Decoder
A Viterbi decoder makes use of the Viterbi algorithm to decode the bits stream produced by a convolutional encoder. They are capable of minimizing Bit Error Rate (BER) to a great extent. A Viterbi encoder includes surplus information in the transmitting signal. This further reduces the probability of errors in the received signal that may be corrupted by noise [13].
An Adaptive Viterbi decoder can also be implemented in any communication system. They can minimize the total power consumption when compared to a conventional Viterbi decoder. It has been proved that the power utilization can reduce drastically to 20% where as in Viterbi decoder the power consumed is around 80% [14]. This is achieved at cost of increased design time. Also it is useful only when the constraint length is large.
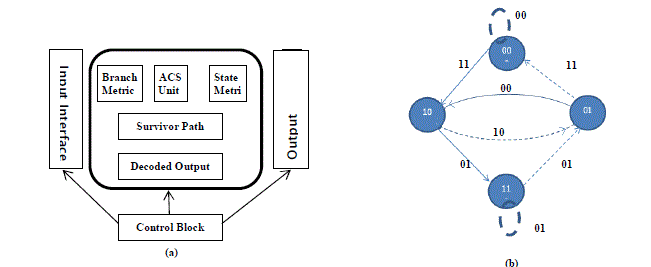
A Viterbi decoder consists of five major building blocks [13]:
• Input output interface block: The I/O interface block provides necessary analog to digital conversion and synchronization.
• Branch metric computation block: The branch metric computation block computes the branch metrics for each branch.
• Add-Compare-Select (ACS) block: The ACS block generates the survivor path information using the new branch metric and current state metric.
• Survivor path storage block: These stores the best path obtained from back-tracing procedure applied to the trellis structure. The ACS unit identifies path with lowest cost metric. The survivor path storage block stores the corresponding bit-sequence of the lowest cost paths. This path is based on decisions computed by the ACS unit.
• The output sequence generator block: The output sequence generator block estimates the original input sequence applied to the encoder.
The data bit streams sent by the transmitter are conceived as a sequence of voltage samples. Without loss of generality, it is assumed to be 1 sample per bit. Since the received signal is a voltage, therefore it can be analog. Thereby it becomes necessary to quantize it into several voltage levels so that it can be processed digitally.
The quantization levelling can be done in two ways as described in the next section.
Hard Decision/Soft Decision Decoding: Whenever, the received voltages are digitized before decoding the received bit sequence, then the process is known as hard decision decoding. If the voltage samples are directly decodes before digitizing the received bit sequence then we term such kind of process as soft decision decoding[15]. In hard decision, the received signal is converted into only two levels, i.e. level 0 and level 1. On the other hand in soft decision, the input signal is quantized into more than two levels. Among the two, soft decision performs better as it can capture more information of input signal at the cost of higher complexity.
Generation of Decoded Output Sequence: There are two approaches for generation of decoded output sequence, register-exchange and back-trace[16]. In the register-exchange approach each state has a register to store the survivor path information. These registers are updated for each new code symbol received. So when a complete code word is received, decoded output sequence is readily available. In the back-trace scheme, only the survivor path information for each state is stored for each code symbol. Once the complete code word is received, a trace-back block extracts the decoded output sequence using the survivor path information [17].
There are two different methods for the back-trace approach, shift update and selective update. In shift update method, the survivor path information is shifted in to the registers. In selective update method the survivor path information is routed by a multiplexer to appropriate registers. The author has shown that the power dissipation of the registerexchange and trace-back approaches and the power dissipation of shift and selective update methods [13]. When updating the survivor path matrix, the key issue is that the content of each register does not change as soon as it is updated. This can benefit for low power design of Forward error control approach. This happens due to the fact that there is no need to activate the registers after updating hence the switching activity reduces decreasing power dissipation. This can be realized by applying clock gating-scheme [18].
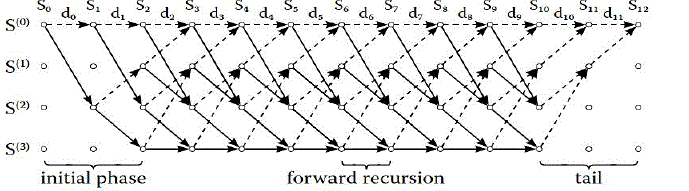
Trellis Diagram: A matched decoding scheme for convolutionally encoded transmission is required at the receiving end. The Viterbi decoders have proved to best choice among the various competing schemes. The size of the trellis diagram is governed by the length of the input sequence i.e. the hardware complexity increases in the order of 2k with the constraint length K. In a conventional Viterbi decoder, there are 2K-1 possible paths required to be calculated in each trellis.
The trellis diagram (Fig 2) represents the state diagram of Figure 4. For each input information symbol dk, the trellis diagram contains all possible state transitions corresponding to the previous encoder state. In figure 4, the dashed edges depict state transitions where dk = 0 and the solid edges represent state transitions where dk = 1 The trellis illustrated in Figure 5 assumes that the first state of the encoder is state S(0). The trellis diagram can be divided into three phases: For a message of the length L, after the initial phase of M encoded bits dk, there are L - M identical trellis segments. After L encoded bits, the encoder is forced to the all zero state by adding a tail of M ‘0’ symbols. This technique improves the error protection of the information symbols at the end of encoded message.
Viterbi Algorithm: The Viterbi algorithm is used to find the most likely path to determine the hidden input states. The algorithm is used to estimate a measure of similarity through the hamming distance between the received signal, at time ti and all the possible trellis paths entering each state at time ti. These distances are known as Hamming distances. Hamming distance is equal to the number of bits, a bit combination differs from the other combination [19].

PROPOSED WORK
In this work, the Maximum-Likelihood algorithm with the hard decision has been employed. Hard decision decoding is capable of deciding whether the bit is 0 or 1 at an early stage. However errors in the received bit sequence may be introduced as the decoder may take wrong decisions for voltages near threshold.
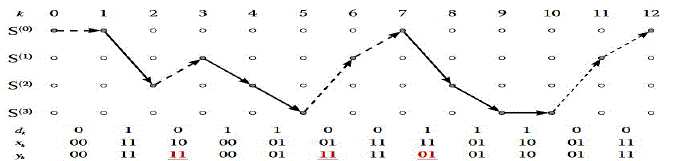
Decoding With Viterbi Algorithm: In this work, the input bits dk are encoded using the rate 1/2, non-systematic, nonrecursive convolutional encoder. The output symbols Yij were transmitted on a channel with AWGN. During the data transmission, suppose three of the received symbols got corrupted (underlined, bold red).
All the corrupted bits can be restored to their correct values during the trace-back procedure in Viterbi decoding. This can be easily extricated from Figure 7.

A COMPARATIVE STUDY: ASIC, DSP, MICROCONTROLLER, FPGA
Any design engineer seeks to minimize simultaneously four factors:
• The number of transistor used,
• The number of clock cycles required to execute the whole design,
• The total design time taken to develop the application, and
• Non-Recurring Engineering Costs.
The four technologies face four challenges as mentioned above. These have certain tradeoffs in achieving the four optimization goals. For delivering any standard application the closest match is always chosen. During development phase or prototyping FPGA or MCU/DSP plus FPGA solution is always preferred. By using a FPGA a massive parallel execution of the code can be employed, hence an increased throughput. This is possible due to the fact that unlike a microprocessor which deploys its code to be executed sequentially, FPGA executes the whole code at once. Hence, a FPGA can offer a massive parallel execution thereby increasing the throughput of the program. In this work the code is implemented on FPGA Spartan 3E (XC3S250E-4-PQ208) board. The Viterbi algorithm has a high complexity for computation, but it does the maximum likelihood decoding. Since FPGA has large number of input output ports along with large number of configurable logic block, hence FPGA is most suited for Viterbi decoding. Other benefits of FPGA that are being utilized are based on the fact that lies in achieving all these standards either at a moderate level or a top level without any significant tradeoff.

REQUISITES/ADOPTED METHODOLOGIES
For the proposed work, an integration of correct hardware and software is required for device to function appropriately. Owing to the high number of slices, flip flops and LUTs (Look Up Table), Spartan-3E FPGA (XC3S250E-4-PQ208) has been programmed. The timing waveform has been verified on ModelSim SE-EE 6.4a simulation software. The RTL (Register Transfer Level) code is synthesized using Xilinx ISE 8.1i web-pack. The generated bit file is used to program FPGA board via parallel port using JTAG cable. The use can apply the input by pressing the switches. The output is seen by the glowing LEDs (Light Emitting Diodes).
The summary of hardware and software being used has been summarized as below.

Hardware Used:
• Spartan-3E FPGA (XC3S250E-4-PQ208)
• JTAG Cable.
• Eight individual LED to show output.
• On-off switches for applying input.

Software Used:
• Xilinx ISE 8.1i for synthesis and implementation.
• ModelSim SE-EE 6.4a for simulation

WORKING
The Convolution encoder adds redundant bits to the data being transmitted. The output of the encoder is sent after some processing before the final transmission through the channel. The Viterbi decoder takes the received information bit to measure the distance and calculates the most likely transmitted signal. The Viterbi Algorithm removes those trellis paths that could not possibly be candidate for the maximum likelihood choice. In case the two paths derived have the same state, the one having the least path metric is chosen. This selected path is termed as the surviving path.

RESULT AND DISCUSSION
The design flow followed to accomplish the designing process is similar to the one used in industry. The behavior of both convolution encoder and Viterbi decoder has been described in VHDL. This process was followed by the synthesis of the description of design to generate a gate level circuit. This RTL gate level synthesized circuit is placed and routed on Spartan 3E development board.
The simulation of the Convolution encoder and Viterbi decoder is verified on Modelsim SE 6.4a digital simulating software. With the satisfaction of the functional verification of design, the encoder and decoder are synthesized using Xilinx ISE 8.1i webpack. After synthesizing the entire circuit model is processed through Translate, Map, Place and Route successfully. Later a UCF file of the target object is created which is prototyped with hardware FPGA Spartan 3E hardware, through parallel connection using JTAG. Boundary Scan is performed in the graphical view in iMPACT. Finally the VHDL code is successfully configured into the FPGA. Results obtained were correct as per expectation

A. Simulation Results
The behavioral and timing simulation of the design has been performed and there results are shown in the next two sections.
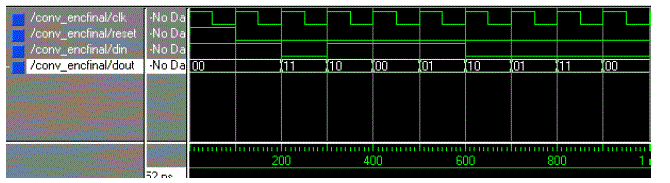
Convolution Encoder: The input data stream “10111000” went through the designed convolution encoder (3,1,2) to give output bit stream “11 10 00 01 10 01 11 00”. The output contains redundant bits to reduce probability of error introduced by additive white Gaussian noise.
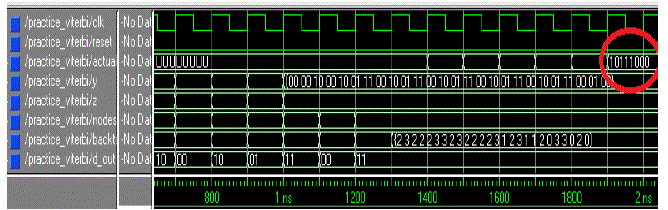
Viterbi Decoder: At the receiver side when received bits are “11 10 10 00 10 01 11 00” with errors in 5th and 8th bits, the error was automatically corrected by Viterbi decoder. The transmitted data “10111000”is successfully obtained as marked in simulation results.

B. Synthesis Report:
From the synthesis report (Fig. 9) it can be seen that the netlist generation has been carried out successfully.
The chip utilization being a low value, some extra circuitry can also be embedded on FPGA board to accomplish greater or bigger tasks in conjunction with the Convolution Encoder and Viterbi decoder.

CONCLUSION
From the simulation results it can be concluded that the hard decision technique can detect any multiple number of errors which is most likely to occur inside the transmitting media due to presence of an Additive White Gaussian Noise(AWGN). They proves to be effective in minimizing forward error in a typical Communication system. The design developed is based on hard decision decoding and reasonable hardware complexity i.e. a Constraint Length of K = 3. The results obtained from synthesis, simulation and hardware testing were accurate, error-free in recovering the original information successfully.
 

Tables at a glance
Table icon Table icon
Table 1 Table 2
 

Figures at a glance


Figure Figure Figure Figure
Figure 1 Figure 2 Figure 3 Figure 4
Figure Figure Figure
Figure 5 Figure 6 Figure 7
 

References