Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

An Image Compression Technique Based on the Novel Approach of Colorization Based Coding

Shireen Fathima1, E Kavitha2
  1. PG Student [M.Tech in Electronics], Dept. of ECE, HKBK College of Engineering, Bangalore, India
  2. Research scholar, St. Peter’s Institute Of Higher Education And Research, St. Peter University, Avadi, Chennai, India Professor, PG-coordinator, HKBKCE, Bangalore, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In this paper, we formulate a method for the colorization-based coding problem . Previously, several colorization methods have been proposed to colorize grayscale images using only a few representative pixels provided by the user. An encoder extracts RP from an original color image and transmits RP and all luminance components (compressed by the conventional encoder) to a decoder. Then, the decoder restores a color image by colorization Obviously, to implement colorization-based coding, automatic RP extraction is required, and which extraction method is chosen determines the performance of the colorization-based coding method. In this paper the colorization-based coding problem is formulated into an optimization problem, i.e., an L1 minimization problem .By formulating the colorization-based coding into an L1 minimization problem, it is guaranteed that, given the colorization matrix, the chosen set of RP becomes the optimal set in the sense that it minimizes the error between the original and the reconstructed color image. We construct the colorization matrix that colorizes the image in a multiscale manner. Experimental results revealed that our method can drastically suppress the information amount (number of representative pixels) compared to conventional colorization based-coding and outperforms conventional colorizationbased coding methods as well as the JPEG standard and is comparable with the JPEG2000 compression standard, both in terms of the compression rate and the quality of the reconstructed color image.

Keywords
Image colorization, representative pixels, image compression, reconstruction

INTRODUCTION
Images are extensively being used day to day in various fields and the periphery of application is also increasing. With the advent of internet and WWW, there was a need to transmit images and other multimedia objects over the network and for this came various compression techniques to achieve better throughput. Some of these techniques focused on high compression ratio while other on better quality and appreciable compression ratio. In recent years, several methods called colorization have been proposed [1][2][3] for adding color to a given grayscale image from a few pixels that have color information. We denote these pixels as representative pixels (RP), and RP can be represented by the positions and color values of these pixels. Since the information amount for representing positions and color values of RP is small, a novel approach to image compression by using colorization (called colorization-based coding) has been researched [4][5][6]. The main task in colorization based compression is to automatically extract these few representative pixels in the encoder. In other words, the encoder selects the pixels required for the colorization process, which are called representative pixels (RP) in [4], and maintains the color information only for these RP. The position vectors and the chrominance values are sent to the decoder only for the RP set together with the luminance channel, which is compressed by conventional compression techniques. Then, the decoder restores the color information for the remaining pixels using colorization methods.
The main issue in colorization based coding is how to extract the RP set so that the compression rate and the quality of the restored color image becomes good. Several methods have been proposed to this end [1]–[4]. All these methods take an iterative approach. In these methods, first, a random set of RP is selected. Then, a tentative color image is reconstructed using the RP set, and the quality of the reconstructed color image is evaluated by comparing it with the original color image. Additive RP are extracted from regions where the quality does not satisfy a certain criterion using RP extraction methods, while redundant RP are reduced using RP reduction methods. However, the set of RP may still
contain redundant pixels or some required pixels may be missing. In this paper, we present a new colorization-based coding method. Our method minimises the number of pixels in the RP set by using the L1 minimization.The optimal set of RP is obtained by a single minimization step, and does not require any refinement, i.e., any additional RP extraction/reduction methods. Therefore, there is no need for iteration. Furthermore, there is no need to use a geometric method such as defining line segments or squares as in[8-9]. It will be shown experimentally that the proposed scheme compresses the color image with higher compression rate than the conventional JPEG standard as well as other colorization based coding methods, and is comparable to the JPEG2000

RELATED WORKS
Colorization is a technique which adds color components to grayscale images using the color assignation provided by users. To understand the proposed method, four major related works have to be explained.
A.Color Image Coding
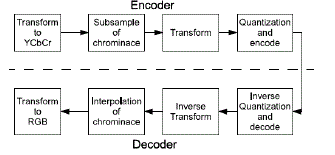
An overview of conventional color image coding methods is shown in Fig.1.
At the encoder, original images are transformed from the RGB color space to the YCbCr color space. The human visual system is sensitive to changes of not chrominance, but luminance. To reduce the amount of information, from this property, chrominance components (Cb, Cr) are generally subsampled. Luminance and subsampled chrominance are transformed into the frequency domain, and then quantized and encoded. At the decoder, images are reconstructed by inverse processes[10].
At the decoder, subsampled chrominance should be interpolated. In the conventional methods, linear interpolation methods are used. Therefore, decoded chrominance components blur near edges.
B. Levin’s Colorization
Levin et al’s colorization algorithm is based on a simple premise: neighboring pixels that have similar intensities should have similar colors. Consider the YCbCr color space. Y is the luminance component corresponding to y, and Cb or Cr is the color component corresponding to u. Let n be the number of pixels in the original image and r be an identifier of the pixels in raster-scan order (1 ≤ r ≤ n). u (u ∈Rn) is assumed to be a one-dimensional vector that contains a color component restored by colorization (denoted as the restoration color component) and is arranged in column in raster-scan order. x (x ∈Rn) is assumed to be a one-dimensional vector that contains RP values, and x has non-zero values only for RP. u(r) and x(r) are the r-th elements of u and x respectively. Ω = { r/x(r) ≠0} is a set of positions of RP. Obviously, |Ω| is the number of RP that have a specific color value, and it corresponds to the amount of information in-colorization based coding. Let y(r) be a luminance component at the r-th pixel. s ∈ N(r) denotes that the s-th pixel is belonging to the neighbor (defined as 8 surrounding pixels) of the r-th pixel. Levin et al defined a cost function as
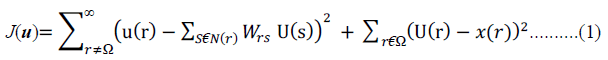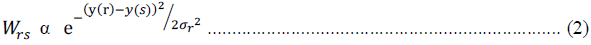image
image
Where Wrs is a weighting function that sums to one.
Figure 2 shows Levin et al’s colorization method. The user have to manually put scribbles on the image regions as in 2(a) then the algorithm colors the whole image. It is a manually intensive and time consuming process.
C. Colorization-based Coding by Cheng et al
Cheng et al’s colorization-based coding uses an active learning approach to extract RP automatically. Their method perform better than JPEG for color components. The steps of their method are given below.
1. Divide original image into clusters by image segmentation algorithm.
2. Extract RP randomly from each cluster.
3. Conduct colorization by using temporary RP.
4. Search for clusters that have high error between original and colorized images.
5. Extract more RP from high-error clusters.
6. Repeat 4–5.
Additionally, Cheng et al apply some extension to Levin’s colorization to suit their approach. However, their colorization-based coding cannot reduce the redundant RP if the initial RP (extracted at step 2) already have redundancy.

PROPOSED METHOD
While most colorization based coding methods try to extract the RP set by using an iterative approach[12], we formulate the RP selection problem into an minimization problem. An essential prerequisite for this is that the colorization matrix has to be determined beforehand.
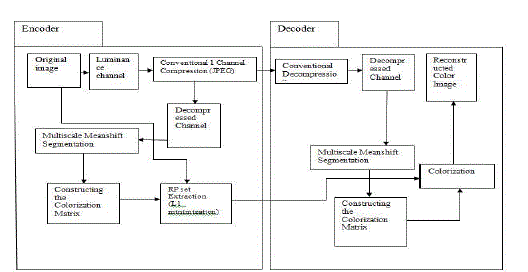
Figure 3 shows the overall system diagram of the proposed method.
The original color image is first decomposed into its luminance channel and its chrominance channels in the encoder. Conventional one-channel compression techniques, e.g., JPEG standard is used to compress the luminance channel and its discrete Fourier or Wavelet coefficients are sent to the decoder. Then, in the encoder, the colorization matrix C is constructed by performing a multi-scale mean shift segmentation on the decompressed luminance channel. The decompressed luminance channel is used to consist with that in the decoder. Using this matrix C and the original chrominance values obtained from the original color image, the RP set is extracted by solving an optimization problem, i.e., an L1 minimization problem. This RP set is sent to the decoder, where the colorization matrix C is also reconstructed from the decompressed luminance channel. Then, by performing a colorization using the matrix C and the RP set, the color image is reconstructed.

EXPERIMENT RESULTS
To make the visual comparison easy, we constructed the colors with a very small number of coefficients (or RP) for all the methods. In the comparison with conventional colorization based coding methods, we used an uncompressed luminance channel in the reconstruction of the color image for all methods. The proposed method surpasses other colorization based coding methods by a large amount, and using a compressed luminance channel makes no difference in the comparative result.
Figure 4(a) to (F) shows the results of the implementation in MATLAB_2012b.
Figure 4(a) shows the original peppers image which is first decomposed into YCbCr color space resulting in Y, Cb ,Cr components as shown in fig 4(b),4(c), 4(d)respectively
Figure 4(e) shows the result of performing the meanshift segmentation which is used to easily generate segmented regions of different photometric and spatial characteristics[13]and figure (f) shows the reconstructed color image after performing colorization.we can observe that the quality of the reconstructed image is visually good.
The results can also b obtained by designing a graphical user interface in the matlab-2012b as shown in figures 5(a) to 5(c) below.
Fig. 5(a) represent the Graphical user interface which is a graphical display in one or more windows containing controls, called components that enable a user to perform interactive tasks. Figure 5(b) shows original image being decomposed into its luminance(y) and two chrominance components(Cb,Cr)
Fig 5(c) shows the reconstructed luminance component and the reconstructed color image respectively along with the SSIM values for the chrominance components and the PSNR value obtained by the proposed method . Table 1 gives the comparision of the proposed work with jpeg and jpeg2000 standards. We use the peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) value as an objective evaluation of image quality for comparision. PSNR is defined as
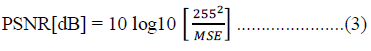image
where MSE is a mean squared error. SSIM is the image quality assessment based on the degradation of structural information, better for the human visual estimation than traditional image quality assessments such as PSNR. SSIM between images X and Y is defined as
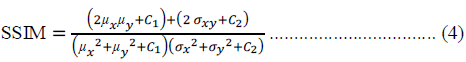image
Where μx is the average of X and μy is the average of Y. σxy is the covariance of X and Y. σx is the variance of X and σy is the variance of Y. C1 and C2 are constants. Result numbers are averages of PSNR and SSIM of the three RGB components. Using a compressed luminance channel deteriorates the PSNR a little compared with that using an uncompressed luminance channel.
The file sizes of the images compressed with JPEG/JPEG2000 standards are the sums of the compressed luminance channel and the chrominance values together. With the proposed method, the file size is the sum of the compressed luminance channel .

CONCLUSION
The majority of existing colorization algorithms focuses on extracting the representative pixels from an original color image at an encoder and restores a full color image by using colorization at a decoder. However, colorization-based coding extract redundant representative pixels and do not extract the pixels required for suppressing coding error. Our studies have demonstrated the importance of automatically extracting representative pixels by using optimization. We have also observed that the selection of the RP is optimal with respect to the given colorization matrix and donot require iterations. By formulating the problem as an optimization problem we have opened the way to tackle the colorization based coding problem using several well-known optimization techniques. However, the problem of computational cost and use of large memory remains, and has to be further studied.
 

Figures at a glance
Figure Figure Figure Figure Figure
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
 

References