Besides the hardware complexity and hence increased power consumption, M-ary modulation schemes ensure improved performance and bandwidth efficiency. But, in wireless sensor networks where power consumption is a critical issue, it is required to consider non-coherent M-ary schemes together with the possible ways of improving their performance. This paper is a study of BER performance of Reed-Solomon Coded M-ary frequency shift keying (MFSK) under AWGN, multipath Rayleigh and Rician fading channels. Simulations were run using Matlab/Simulink model. The simulation results show that, Binary input RS Encoder-Decoder provides improved BER when compared to that of Integer input RS Encoder-Decoder, especially for the preferred smaller values of M.
Keywords |
| MFSK, Reed-Solomon Code, BER, Rayleigh, Rician |
INTRODUCTION |
| The environment of interest is being sampled continuously by a dedicated sensor node and this sensed physical
parameter should be transmitted, preferably equal amount of data per unit time to a designated sink node. Such a
proactive sensor network is the scenario for many environmental parameters like contamination level, surrounding
temperature and radiation from the sun. In its active mode duration, the sensed signal which is in analog form (after the
conversion of raw data from the sensors by the transducer) is first converted into its corresponding digital version by an
Analog-to-Digital Converter (ADC). And from this digitized data, an N-bit message sequence is generated, modulated
using any prioritized modulation scheme. This modulated data is transmitted to the sink node via the channel. After this,
the sensor node goes into its sleep mode during which all the components of transceiver circuitry are shut down to
conserve the charge in the battery. |
| The duration of this transient mode is the sum of the switching time from sleep mode to active mode and the
negligible switching time from active mode to sleep mode. In order to transmit the sensed data, whenever the sensor
node transits from its sleep mode to active mode, a considerable amount of power is consumed to start up the
transmitter, while the power consumption during the transition from active mode to sleep mode is negligible. As far as
energy efficiency of transceiver circuitry designed for wireless sensor nodes is concerned, the main focus is on the
modulation block. Energy consumption of transceiver circuitry can be reduced in several ways. |
| The reduction of transmit on-time of the transceiver can increase the energy efficiency of communication.
Transmit on-time can be lowered by transmitting multiple bits per symbol and this is accomplished by using M-ary
modulation schemes. But, this increases the hardware complexity of transceiver and also its power consumption. |
| In general, the receiver circuitry in traditional M-ary modulation schemes like MQAM, M-PSK is more
complex. When such a complex receiver circuit is implemented on sensor nodes, they consume more power besides
their appreciable Bit-Error-Rate (BER) performance. In addition to this, they require some of the most power intensive
components such as Digital-to-Analog Converters (DACs) and mixers in the receiver circuitry [7]. The significance
towards the achievement of comparatively less complex transceiver circuitry with MFSK is possible as this scheme can
be implemented digitally inside the frequency synthesizer. Because of this, MFSK has faster start-up time than other
pass-band schemes. |
| The output of the frequency synthesizer is frequency modulated and controlled simply by „b‟ bits in the input
of a digitally controlled block. The modulated signal is then filtered again, amplified by the Power Amplifier (PA), and
finally transmitted to the wireless channel, as illustrated above in Fig.1. |
| The rest of this paper is organized as follows: Section II gives a brief overview about MFSK and an idea about
its performance over AWGN, multipath Rayleigh and Rician fading channels with Reed-Solomon FEC. Section III
explains the role of RS code in this simulation. Section IV is for explaining the simulation setup used here. Section V
details the simulation resuts and Section VI concludes this paper. |
MFSK, AWGN and Fading Channels |
| In a modulation scheme, when the orthogonal signals over any specific time period T are harmonics of any
frequency 1/T, such a modulation scheme is referred as “Multi-frequency shift keying (MFSK)”. As there is no need to
get synchronized with the phase of the transmitted carrier, the receiver can distinguish a maximum of
M = (BW)*T orthogonal signals, where BW is the bandwidth of the system. This capability of orthogonal signal
separation is half of that of coherent receiver. Anyone of M=2m orthogonal signals Sm(t); m=1,2,...,M modulates the
carrier cos(2πf)t during each interval of time T. |
| Moreover, M-ary FSK modulator does not require Mixer and Digital-to-Analog Converter, as it uses M=2m
orthogonal signals. Due to this, M-ary FSK scheme is referred as Direct Digital Modulation (DDM) approach [7]. This
enables M-FSK to have faster transition from sleep mode to active mode when compared to other M-ary modulation
schemes. As the phase is not needed to be continuous in Multiple Frequency Shift Keying (M-FSK), variations in these
multiple frequencies are totally unpredictable. In general,, M is a non-zero power of 2 and Cartesian Coordinates are
used to characterize the complete signal set such that all the sinusoids with respective assigned frequency is represented
by mutually perpendicular axes. There will be a total of M=2K code symbols with K as the number of data bits per
symbol for any (N, K) RS code [1]. Then FSK modulation for each signal can be expressed generally as, |
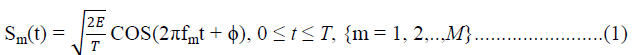 |
| So, it is convenient now to map each code symbol produced at the output from encoder to anyone of the M
frequencies in the set of M-FSK signals. With T as the time required to transmit anyone of the M frequencies or each
code symbol, the transmission rate can be expressed as, |
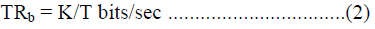 |
| and the corresponding information rate can be expressed as, |
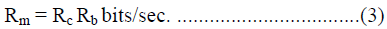 |
| where Rc, code rate = K / N. Additive White Gaussian Noise is the appropriate model to represent the thermal noise at
the receiving end. Then the relationship between channel input and output can be expressed as, |
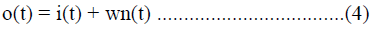 |
| where i(t) is the channel input as a function of time t and wn(t) is the White Gaussian Noise, which gets added to i(t)
and produces o(t). The capacity C of Additive White Gaussian Channel can be expressed as, |
 |
| where BW is the bandwidth of the channel and SNR is the signal-to-noise ratio [1]. |
| When M-ary FSK is employed in a communication system suffers from slow fading i.e. any block of data
with K symbols undergoes a constant, random fade with each symbol constellation consists of number of symbols
M=2n where n is any positive integer, then the received symbols can be represented as, |
| with i as the time index, A as the amplitude of the complex signal which is assumed to be constant over the entire frame
and Ni as the noise vector whose elements are drawn from a zero mean complex Gaussian distribution with a variance
of N/2 per real dimension. Here Ri, Si and Ni are vectors with a dimension of M x 1 and for Si = [0,...,0, 1,..., 0, 0]T
,
with mi as the position of 1 such that (1 ≤ mi ≤ M). And mi indicates that the symbol is transmitted at time i, while zero
is represented for the remaining positions. |
REED-SOLOMON CODES |
| Basically, Reed-Solomon codes are non-binary systematic cyclic linear block codes. They are cyclic because
each valid code produces another valid code when it is circularly shifted. They are linear because a new code word with
the same length can be generated by adding any two valid code words. As the RS encoder processes each block of
message symbols, represented as a sequence of m-bits with m as any positive integer which is greater than 2, these
codes are referred as Block codes. And each R-S (N, K) code, where „N‟ represents length of each block, and „K‟
represents the number of original message symbols, on m-bit symbols exist for all N and K such that 0 < K < N < 2m +
2. As the error correction is on symbol level, these codes are suitable for correcting burst errors. Suitable reversible
mathematical function is applied to the message symbols by the RS encoder so as to generate redundant or parity
symbols such that the number of parity digits N-K = 2t. Then these redundant symbols are appended on to the message
symbols to form the code word. The minimum distance between two different codes is, d = 2t+1. Due to the availability
of sufficient and efficient encoding techniques, cyclic codes are used in several applications. Reed-Solomon codes are
much useful for burst-error correction as they deal with symbols or they are block level codes. They are very much
effective for channels with memory. |
| R-S code has an interesting feature that any amount of two information symbols can be added with any R-S
code with length „N‟ while the minimum distance between codes is maintained. Now, the new R-S code will have a
length of „N+2‟ with equal amount of parity check symbols as the original code. According to the concept of R-S codes,
encoding of „K‟ message symbols is done by viewing them as coefficients of any polynomial m(x) of highest degree K-
1 over a finite field of order „x‟. After this, the polynomial is evaluated at N>K distinct points. When this polynomial
with degree K-1 is sampled at more than K points, a over-determined system is created. But in real-time scenario, rather
than transmitting sampled values of a polynomial, these encoded symbols are viewed as the coefficients of an output
polynomial C(x) which is constructed after the multiplication of message polynomial m(x) of maximum degree K-1 by
a generator polynomial g(x) of degree t=N-K-1. When a generator polynomial g(x) can be defined with its roots α, α2, . .
. αt i.e. g(x) = (x + α) (x + α2)...(x+ α2t) then the transmitter will send the x-1 coefficients of C(x) = m(x)g(x) [2]. There
are two basic classifications of R-S decoding algorithms – frequency domain, time domain. Due to the need of
additional error value transformation block, inverse transformation block and delay block for syndrome polynomial,
implementation of frequency domain algorithm requires more chip area which leads to more power dissipation than
time domain algorithm. |
| According to the method for solving Error Locator Polynomial, the time domain algorithm can further be
divided into two classes – Euclidean algorithm and Berlekamp-Massey algorithm [6]. As BM algorithm needs only
fewer gates for its implementation, it provides less implementation complexity and so it has less critical path delay.
Even though, Euclidean algorithm requires comparatively simple structure for its implementation, it requires a
considerable number of logic elements for implementing the polynomial division function. |
SIMULINK MODEL |
| With reference to [5] and as shown in Fig.2, the Random Integer Generator generates random integers which
are replica of the sensed data from the sensors. This data is then applied to the input port of Reed-Solomon Encoder,
before which the randomly generated data is converted to the suitable needed form, as per the type of encoder i.e.
whether its input should be Integer or Binary. This encoded data modulates the carrier signal at the M-ary Frequency
Shift Keying modulator with the value of M as 2 i.e. two tones. After being propagated into the suitable channel, the
received modulated signal is first demodulated and then decoded. Error Rate is calculated by comparing the actually
transmitted data with the received data and the result is displayed as Bit Error Rate. |
SIMULATION RESULTS |
| The simulations were run for both Integer input RS Encoder and Binary input RS Encoder. When both the
simulation results shown in Fig.3 and Fig.4 are compared, the Binary input RS Encoder gives comparatively improved
BER performance in overall against Integer input RS Encoder. |
| From Fig.3, it is evident that, binary input RS encoder has its worst, almost constant BER performance under
AWGN channel even for the least eligible value of M = 2. BER performances under both multipath Rayleigh and
Rician fading channels are much closer but, to be specific, binary input RS encoder gives its best BER performance
under Rayleigh fading channel over the entire range of Gain Vector. |
| Fig.4, shows that, integer input RS encoder provides its worst BER performance under Rician fading channel
even for M = 2. BER performance under AWGN channel is moderate and almost constant for various values of Eb / No.
And it has its much improved BER performance under multipath Rayleigh fading channel, especially at lower values of
Gain vector and merges with the performance of AWGN at the higher end of Gain Vector. specific, binary input RS
encoder gives its best BER performance under Rayleigh fading channel. |
CONCLUSION |
| Besides the energy efficient performance, the entire communication environment set for sensor nodes in low
power and low duty cycle WPANs, the data being transmitted and received should be robust enough to withstand the
heavy noisy environment in the unlicensed ISM band. In order to fulfil this, reducing the hardware complexity can help
only in less power consumption and of course a quick change over between different state of sensor node operation.
And in order to provide the much required robustness to the data to be communicated, one of the main aspect to be
considered is Forward Error Correction (FEC) codes. It is needed to prove that the FEC scheme considered in this
simulation, Reed – Solomon Encoding – Decoding should be a promising one to fulfil the requirements in terms of less
hardware complexity so that much reduced power consumption and quicker transitions between states. This can be
further verified by proceeding further with the same aspect. |
| |
Tables at a glance |
 |
 |
| Table 1 |
Table 2 |
|
| |
Figures at a glance |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
| |
References |
- SaurabhMahajan, Gurpadam Singh, “BER Performance of Reed-Solomon Code using M-ary FSK Modulation in AWGN Channel”, International Journal of Advances in Science and Technology, Vol. 3, No.1, 2011.
- BingxinShen, “Application of Error Correction Codes in wireless sensor networks”, Master‟s Thesis, August 2007.
- I.Bar – David, S.Butman, “Performance of Coded, Non-coherent, Hard-decision MFSK Systems”, JPL TECHNICAL REPORT, 32 – 1526, Vol. XIII.
- Lionel Biard, Dominique Noguet, “Reed - Solomon Codes for Low Power Communications”, Journal of Communications, VOL. 3, NO. 2, APRIL 2008.
- B. K. Mishra, SukrutiKaulgud and Sandhya Save, “Design of RS Code Using Simulink Platform”, International Conference & Workshop on Recent Trends in Technology, (TCET) 2012 Proceedings published in International Journal of Computer Applications® (IJCA) Bernard Sklar, “Reed – Solomon Codes”, Journal of the Society for Industrial and Applied Mathematics, 1960.
- JamshidAbouei, Konstantinos N. Plataniotis, SubbarayanPasupathy, “Green Modulations in Energy-Constrained Wireless Sensor Networks”, ICASSP Conference, March 2010.
- Padmavathy, M.Chitra, “Performance Evaluation of Energy Efficient Modulation Scheme and Hop Distance Estimation for WSN”,IJCNIS, Vol.2 No.1, April 2010.
- ChinmoyGavini, “Quantifying Tradeoffs in the IEEE 802.15.4 protocol through simulation” Senior Design Project, Summer 2007.
- M. Alnuaimi, K. Shuaib and I. Jawhar, “Performance Evaluation of IEEE 802.15.4 Physical Layer UsingMatLab/Simulink”
|