International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

An M[X]/G/1 Retrial G-Queue with Server Breakdown

A.Divya1, Dr. K. Udaya Chandrika2
  1. Research Scholar, Department of Mathematics, Avinashilingam Institute for Home Science and Higher Education for Women, Coimbatore, Tamilnadu, India
  2. Professsor, Department of Mathematics, Avinashilingam Institute for Home Science and Higher Education for Women, Coimbatore, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Batch arrival retrial queue with positive and negative customers is considered. If the server is idle upon the arrival of a batch, one of the customers in the batch receives service immediately and others join the orbit. If the server is busy, all the customers join the orbit. The arrival of negative customer brings the server down and removes the customer in service from the system. The server is subject to random breakdown while it is working. Using supplementary variable technique, expected number of customers in the orbit and expected number of customers in the system are derived. Stochastic decomposition property is established. Some special cases are discussed and numerical results are presented.

Keywords
Batch arrival retrial queue, G queue, Breakdown, Performance Measures, Stochastic Decomposition

INTRODUCTION
Retrial queueing systems are characterized by the feature that arriving customers who cannot receive service immediately may join a virtual queue called orbit to try their request after some random time. Queueing systems with repeated attempts are found suitable for modelling the processes in telephone switching systems, digital cellular mobile networks, packet switching networks, local area networks, stock and flow etc. Review of retrial queueing literature can be found in the bibliographies of Artalejo (1999a, 1999b) and the books by Falin and Templeton (1997) and Artalejo and Gomez Corral (2008). The applications of retrial queues in science and engineering are given in Kulkarni and Liang (1997). Queue with negative arrivals called G queue was first introduced by Gelenbe (1989) with a view to modelling neural networks. Wu and Lian (2013) analysed an M/G/1 retrial G queue with priority resume, Bernoulli vacation and server breakdown. Using Lyapunov functions. Peng et al. (2013) suggested an M/G/1 retrial G- queue with preemptive resume priority and collisions under linear retrial policy. In this article batch arrival retrial G-queue with server breakdown is analysed.

MODEL DESCRIPTION
Consider a single server retrial queueing system with positive and negative customers. Positive customers arrive in batches according to Poisson process with rate λ+. Negative customers arrive singly with Poisson arrival rate λ-. At every arrival epoch, a batch of k customers arrive with probability Ck. The generating function of the sequence {Ck} is C(z) with first two moments m1 and m2. There is no waiting space in front of the server and therefore if an arriving batch of positive customers finds the server idle, then one of the customers receives the service and others join the retrial queue. If the server is busy, then the arriving batch enters the orbit. 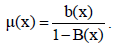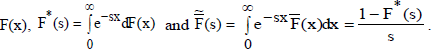The retrial time of the customers is generally distributed with distribution function A(x), density function a(x), Laplace-Stieltjes transform A*(s) and hazard rate function image The service time of positive customers is generally distributed with distribution function B(x), density function b(x), Laplace-Stieltjes transform B*(s) and hazard rate functionimage The arrival of a negative customer removes the positive customer in service from the system and causes the server breakdown. Also the server is subject to unpredictable breakdown while it is working. The life time of the server is exponentially distributed with rate α.The repair time of the failed server is generally distributed with distribution function R(x), density function r(x) and hazard rate function image All stochastic processes involved in the system are assumed to be independent of each other. Throughout the rest of the paper, we denote image the tail of distribution functionimage

STABILITY CONDITION
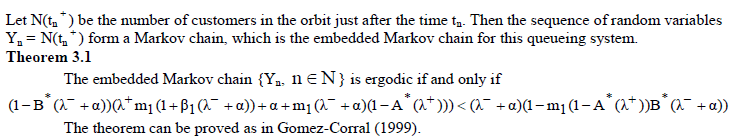image

STEADY STATE DISTRIBUTION
In this section, by treating elapsed service time and elapsed repair time of the server as supplementary variables, the steady state probability generating functions of the orbit size distribution are derived.
Define the states of the server as
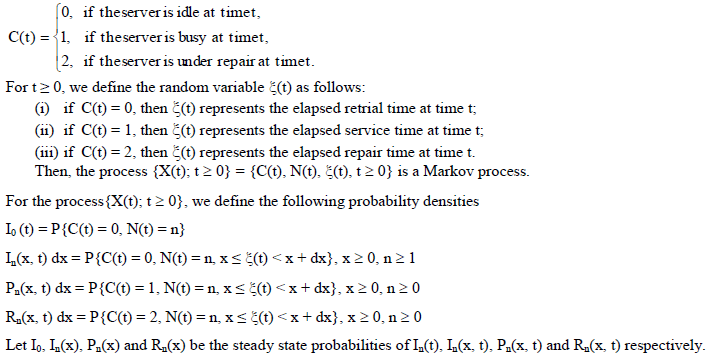image

4.1 The steady state equations
The system of equation that governs the model under supplementary variable technique are given below image
Proof
Multiplying equations (2) to (9) by zn and summing over all possible values of n, we obtain the following equations:
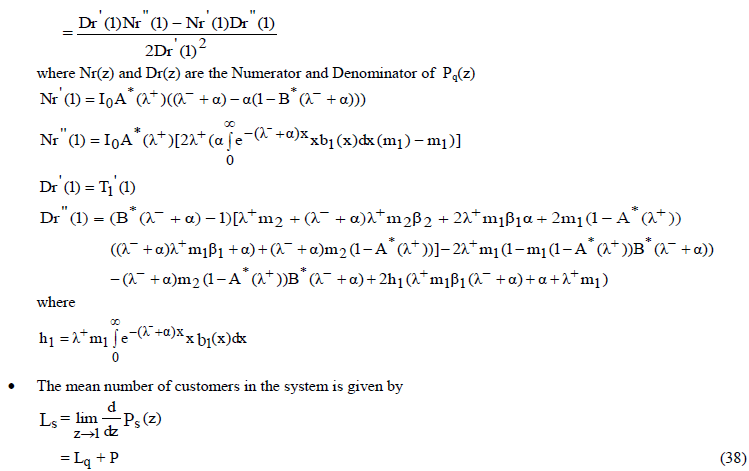image
image
image

STOCHASTIC DECOMPOSITION
The stochastic decomposition property of the system size distribution is verified. The classical stochastic decomposition property shows that the steady state system size at an arbitrary point can be represented as the sum of two independent random variables, one of which is the system size of the corresponding queueing system without server vacations and the other is the orbit size given that the server is on vacations. Stochastic decomposition has also been held for retrial queues.

Theorem 6.2
The number of customers in the system (Ls) can be expressed as the sum of two independent random variables, one of which is the mean number of customers in batch arrival G-queue with server breakdown (L) and the other is the mean number of customers in the orbit given that the server is idle (LI).

Proof
The probability generating function Φ(z) of the number of customers in batch arrival G-queue with server breakdown is given by
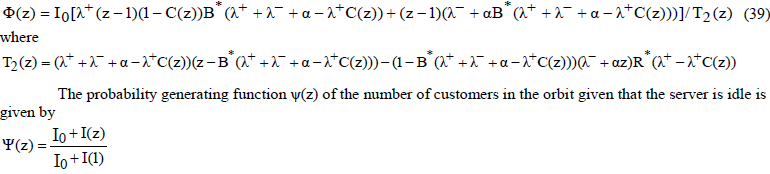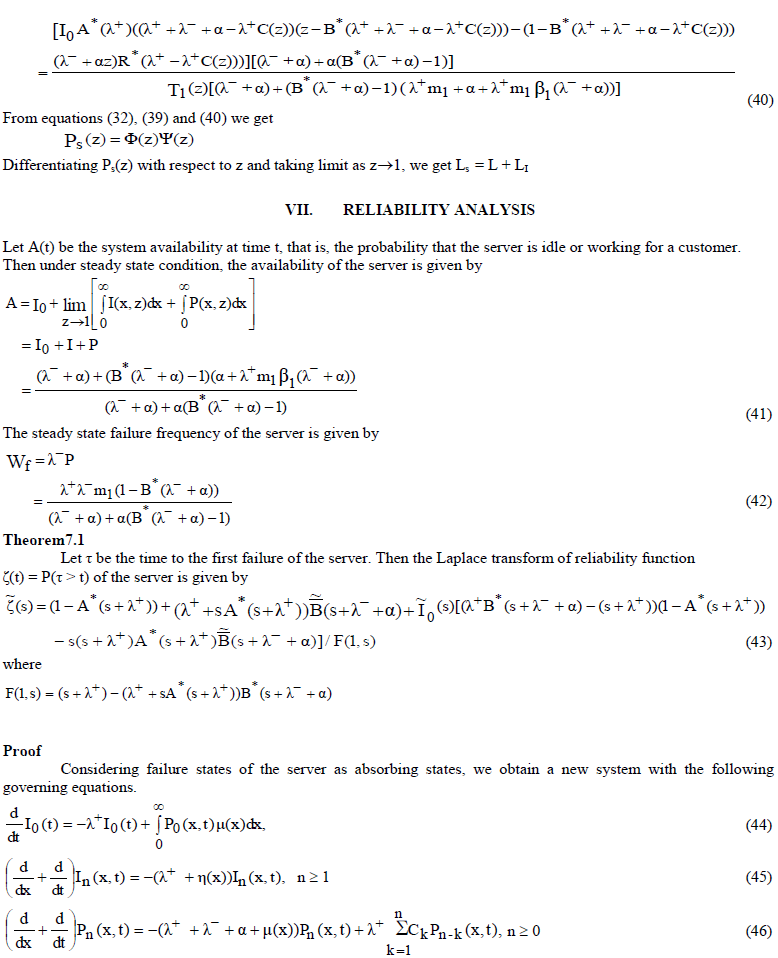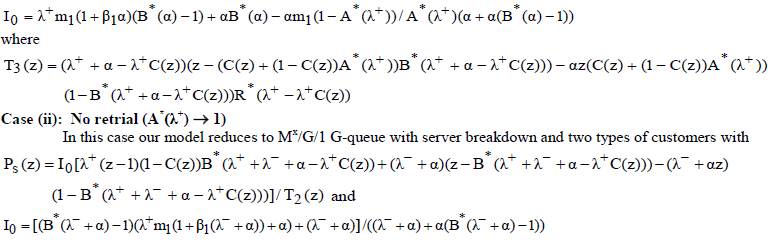image
image
image
image
image

NUMERICAL RESULTS
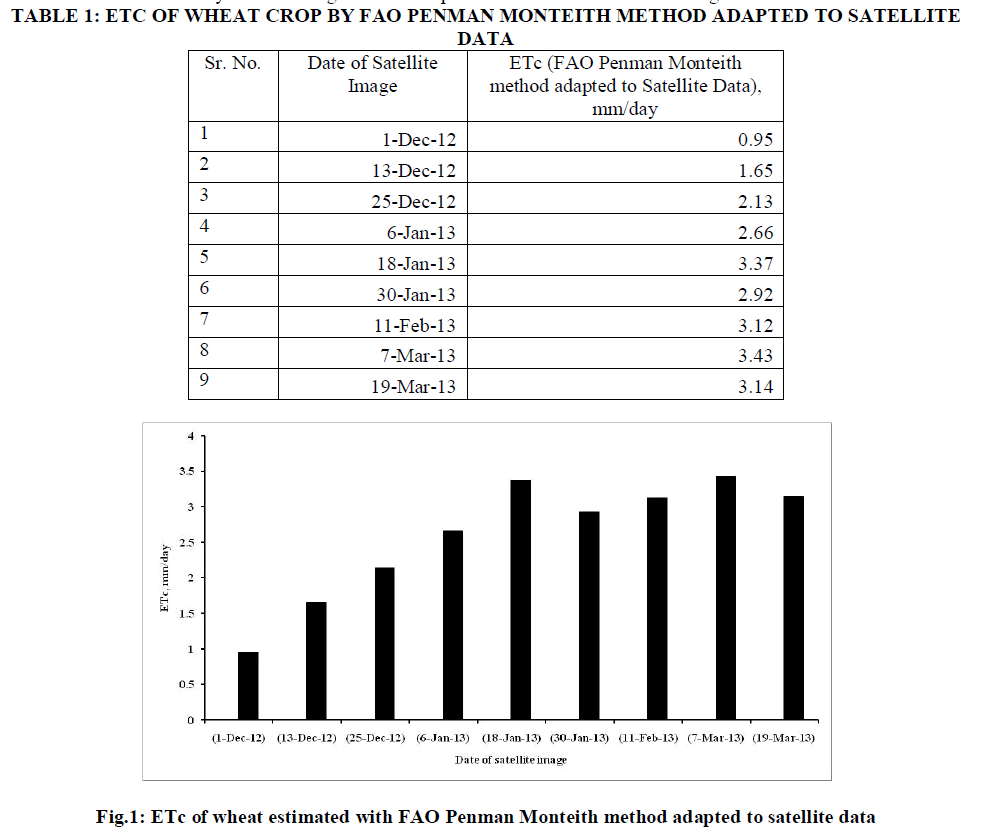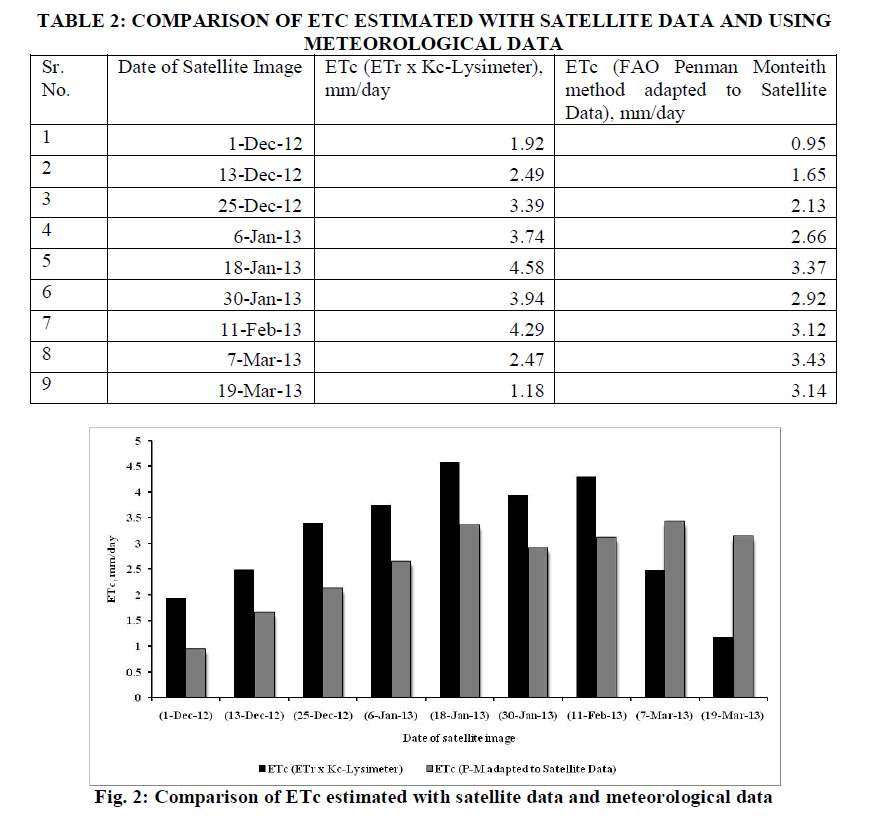image
image
image

CONCLUSION
Batch arrival retrial G queue with server breakdown is analysed. The models considered are investigated using supplementary variable technique to obtain performance measures and reliability indices. Stochastic decomposition law is verified and special cases are discussed. Numerical analysis are carried out to analyse the effect of parameters on the system performance.

References
  1. Artalejo, J.R., “A Classical Bibliography of Research on Retrial Queues : Progress in 1990-1999”, Top, vol. 7, pp. 187-211, 1999a.
  2. Artalejo, J.R., “Accessible Bibliography on Retrial Queues", Mathematical and Computer Modelling, vol. 30, pp. 1-6, 1999b.
  3. Artalejo, J.R., and Gomez-Corral, A., “Retrial Queueing Systems”, Berlin, Heidel Berg, Springer, 2008.
  4. Artalejo, J.R., Joshua, V.C and Krishnamoorthy, A., “An M/G/1 Retrial Queue with Orbital Search by the Server”, Advances in Stochastic Modelling, Notable Publications lnc., NJ, pp. 41-54, 2002.
  5. Chakravarthy, S.R., Krishnamoorthy, A., and Joshua, V.C., “Analysis of a Multi-Server Retrial Queue with Search of Customers from the Orbit”, Performance Evaluation, vol. 63 (8), pp. 776-798, 2006.
  6. Deepak, T.G., Dudin, A.N., Joshua, V.C. and Krishnamoorthy, A., “On an MX/G/1 Retrial System with Two Types of Search of Customers from the Orbit”, Stochastic Analysis and Applications, vol. 31 (1), pp. 92-107, 2012.
  7. Dudin, A.N., Krishnamoorthy, A., Joshua, V.C and Tsarenkov, G.V., “Analysis of the BMAP/G/1 Retrial System with Search of Customers from the Orbit”, European Journal of Operational Research, vol. 157 (1), pp. 169-179, 2004.
  8. Falin, G.I and Templeton, J.G.C., „Retrial Queues, London, Chapman and Hall, 1997.
  9. Gelenbe, E., “Random Neural Networks with Negative and Positive Signals and Product Form Solution”, Neural Computation, vol. 1, pp. 502- 510, 1989.
  10. Gomez-Corral, A., “Stochastic Analysis of a Single Server Retrial Queue with General Retrial Times”, Naval Research Logistics, vol. 46, pp. 561-581, 1999.
  11. Krishnamoorthy, A., Deepak, T.G. and Joshua, V.C ., “An M/G/1 Retrial Queue with Non-Persistent Customers and Orbital Search”, Stochastic Analysis and Applications, vol. 23, pp. 975-997, 2005.
  12. Kulkarni, V.G. and Liang, H.M., “Retrial Queues Revisited”, In Frontiers in Queueing Models and Applications in Science and Engineering, Ed., Dshalalow, J.H., CRC Press, Boca Raton, FL, pp. 19-34, 1997.
  13. Peng, Y., Liu, Z. and Wu, J., “An M/G/1 Retrial G-Queue with Preemptive Resume Priority and Collisions Subject to the Server Breakdowns and Delayed Repairs”, J. Appl. Math. Comput. doi. 10.1007/S 12190-013-0688-7, 2013.
  14. Sumitha, D. and Udaya Chandrika, K., “Numerical Analysis of Two Phase Bulk Arrival Retrial Queue with Orbital Search”, International Journal of Advanced Scientific and Technical Research, vol. 2 (1), pp. 483-493, 2011 .
  15. Wu, J. and Lian, Z., “A Single Server Retrial G-Queue with Priority and Unreliable Server Under Bernoulli Vacation Schedule”, Computers and Industrial Engineering, vol. 64, pp. 84-93, 2013.