ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
S.Palaniyappan1, I.Ilayaranimangammal2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Scarcity of Energy resources, increasing power generation cost and ever-growing demand of electric energy necessitates optimal economic dispatch in today‘s power systems.In this paper presents a computational approach to minimize the total fuel cost in thermal power station using Artificial Immune System (AIS) algorithm. The AIS algorithm is a machine learning approach and a powerful stochastic optimization technique with special features of random search, hill climbing, statistical sampling and competition. The proposed test system consists of six generator units. The analytical computation and simulation of above test system has been performed using the MATLAB environment. The performance analysis of proposed approach is compared with conventional and other optimization algorithms.
Keywords |
||||||
| Economic Load Dispatch (ELD), Artificial Immune System (AIS) Algorithm, Genetic algorithm (GA). | ||||||
INTRODUCTION |
||||||
| The basic objective of economic dispatch of electric power generation is to schedule the committed generating unit outputs so as to meet the load demand at minimum operating cost while satisfying all unit and system equality and inequality constraints. The economic dispatch problem is very complex to solve because of its colossal dimension, a non-linear objective function, and a large number of constraints. The various mathematical programming methods such as Lambda iteration method, participation factors method and gradient methods. Well known long-established techniques such as integer programming [1], [2], dynamic programming [3],[4], and Lagrangian relaxation [5] have been used to solve the economic dispatch problem. Recently other optimization methods such as Simulated Annealing [6], Hopfield Neural Network [7], [8], Genetic Algorithm [9], Particle Swarm Optimization [10] and Tabu Search Algorithm [11] are practiced to solve the economic dispatch problem. | ||||||
| In this paper, a novel implementation of the AIS algorithm is based on pattern recognition and anomaly detection proposed to solve the economic dispatch problems. The effectiveness of proposed algorithm is demonstrated using IEEE 30 bus six generator system considering emission constraints. The implementation of the above algorithm is organized as follows. In section 2, a mathematical formulation of the economic dispatch problem. In section 3, an overview of proposed method using AIS algorithm and their characteristics. In section 4 gives a description of test system. In section 5 includes the simulation results and discussion and conclusions in section 6. | ||||||
PROBLEM FORMULATION |
||||||
| The objective of solving economic dispatch problem is to minimize the fuel cost of electric power system, while satisfying a set of constraints. This can be formulated as follows: | ||||||
a) Problem objective |
||||||
| Minimization of fuel cost: The objective function for the total (Rs/hr) fuel cost can be expressed as | ||||||
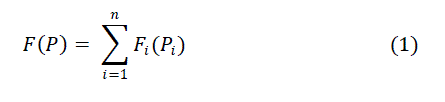 |
||||||
| The fuel cost equation of a generating unit is usually described by a quadratic function of power output Pi as follows: | ||||||
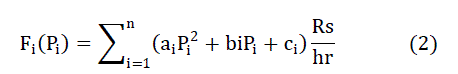 |
||||||
| Where, Fi (Pi) is the fuel cost (Rs/hr), Pi is the power generated (MW) and ai, bi, ciis the fuel cost coefficients ofith unit. | ||||||
b) Problem constraints |
||||||
| Generation capacity constraint: For stable operation, real power output of each generator is restricted by lower and upper limits as follows | ||||||
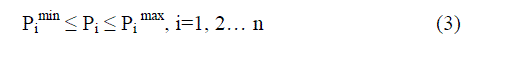 |
||||||
| Power balance constraint: The total power generation must cover the total demand PD and the real power loss in transmission lines PL. Hence, | ||||||
 |
||||||
c) Problem Statement |
||||||
| Aggregating the objective and constraints, the problem can be mathematically formulated as a nonlinear emission constrained single objective optimization problem as follows | ||||||
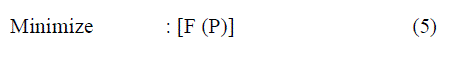 |
||||||
 |
||||||
| Where g is the equality constraint representing the power balance and h is the inequality constraint representing the unit generation capacity. | ||||||
PROPOSED APPROACH |
||||||
| Recently the proposed AIS algorithm can be effectively used to reduce the fuel cost in thermal power station.The AIS can be defined as a computational system based upon metaphors of the biological immune system. | ||||||
a) Artificial Immune System Algorithm |
||||||
| The immune system is a meta-synthesis process that uses the information contained in the problem itself to define the solution tool to a given problem, and then apply it to obtain the problem solution. The topicsinvolved in the definition and development of the artificial immune systems cover mainly: | ||||||
| a) Hybrid structures and algorithms that take into account immune-like mechanisms | ||||||
| b) Computational algorithms based on immunological principles, like distributed processing, clonal selection algorithms, and immune network theory. | ||||||
| c) Immunity-based optimization, learning, self-organization, artificial life, cognitive models, multiagent systems, design and scheduling, pattern recognition and anomaly detection. | ||||||
| d) Immune engineering tools. Potential applications of the artificial immune systems can be listed (but are not limited to): Pattern recognition, function approximation and optimization, anomaly detection, computerand network security, generation of diversity and noise tolerance. | ||||||
IMPLEMENTATION OF THE PROPOSED ALGORITHM |
||||||
| The step by step procedure of AIS for the optimization of generation cost can be outlined as follows: | ||||||
| Step1: Read the data, namely cost coefficients, ai, bi, ci,Pi min&Pi maxof all generating units and population size etc. | ||||||
| Step2:Generate an array of random binary string value. | ||||||
| Step3: Decode the string to actual value. | ||||||
| Step4: Insert them in population pool. | ||||||
| `Step5: Check the satisfaction of constraints of the objective function if ?yes‘ go to (6) else go to (1). | ||||||
| Step6: Evaluate fitness of each set of generation to meet out the demand using the formulae | ||||||
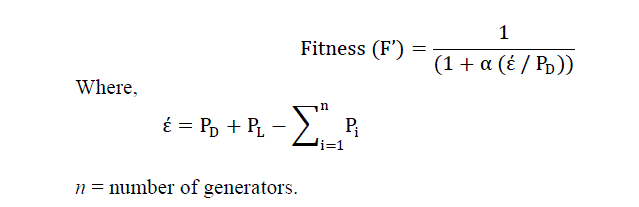 |
||||||
| Step7: Select the antigen and antibody from the fitness values | ||||||
| Step8: Calculate the Euclidean distance between antibody and antigen using | ||||||
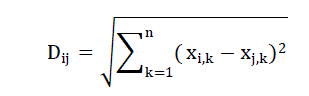 |
||||||
| Step9: If Dij is more select them for hyper mutation else simple mutation by cloning theantibody. | ||||||
| Step10: Enter the cloned population in new population pool. | ||||||
| Step11:Verify the satisfaction of constraints for the objective function. | ||||||
| Step12: Check the convergence else go to clonal proliferation. | ||||||
TEST SYSTEM |
||||||
| The Economic Load Dispatch problem based on Artificial Immune System (AIS) algorithm has applied to the six generator test system. Multiple generator limits and total generation cost of the system is simulated in order to evaluate the correctness and quality of the method.The fuel cost constants and the generator limits of a six generator system are tabulated below, | ||||||
SIMULATION RESULTS AND DISCUSSIONS |
||||||
| `In this paper, the Artificial Immune System algorithm was tested on the standardtest system with six generators for the load demand of 350 MW. Table.3 show that the comparisons of the performance of the AIS algorithm with the Genetic algorithm. | ||||||
CONCLUSION |
||||||
| Economic Load Dispatch problem being attempted using AIS algorithm for six generator test system evaluates the performance of the proposed approach. The solution is analytic in nature with high accuracy and fast computational time. Therefore, this results shows that AIS optimization is a promising technique for solving complicated problems in power system. | ||||||
Tables at a glance |
||||||
|
||||||
Figures at a glance |
||||||
|
||||||
References |
||||||
|