Research & Reviews: Journal of Engineering and Technology
MenuISSN: 2319-9873
ISSN: 2319-9873
+44 7456 035580Biya Motto Frederic1*, Ndzana Benoit2, and Asonganyi Defang Nkafu Austin3
1University of Yaoundé I, Science Faculty, Department of Physics, PO BOX: 812, Cameroon.
2Natioinal Advanced School of Engineering of Yaoundé, Electrical and Telecommunications Department, ACL Laboratory, PO BOX: 8390, Cameroon.
3Mekin Hydroelectric Development Corporation (HYDRO-MEKIN) PO BOX: 13155 Yaoundé – Cameroon.
Received: 11/03/2013; Revised: 14/04/2013; Accepted: 05/06/2013
Visit for more related articles at Research & Reviews: Journal of Engineering and Technology
This paper studies the stability of the roller compacted concrete (RCC) dam of Lom Pangar Project with respect to the sliding, overturning, shearing and seismic forces which exist at the bottom of the river at different times and tries to obtain a safety coefficient. The calculation notes on the stability of the dam have been carried out on 4 block models from different sections of the dam with the aid of the STABCON software developed by COYNE et BELLIER [1]. The stability of the supporting walls of the embankment near the dam was equally verified
Stability, concrete dam, safety coefficient.
Lom Pangar is situated at the confluence of the Lom and Pangar Rivers in the Eastern Region of Cameroon about 420 km east of capital city Yaoundé. The development objective of the Lom Pangar Hydropower Project for Cameroon is to increase hydropower generation capacity and reduce seasonal variability of water flow in the Sanaga River and to increase access to electricity. There are four components to the project: the first component is Lom Pangar regulating dam on the Lom River, the second component is Lom Pangar Power Plant (30MW) and Transmission Line (105Km, 90KV), the third component is environmental and social measures and the fourth component is technical assistance and project management [6].
Our study is interested in the stability of the retaining structure of the dam made of RCC which is 46 meters high and 7m wide at the crest. Following the Cameroon geographic level (CGL), the crest of the dam is at 677.55, the originally defined normal water level 674.50 CGL and the highest water level was 674.55 CGL while the presently fixed normal water level is 672.70 CGL and the highest water level is 673.55 CGL. In this our analysis we used the original values which are higher than the present values thus making our safety analysis more dependable.
A dam can last for hundreds of years. Our concern is to ascertain that the dam is safe enough to stand the test of time and adverse conditions. The stability of the RCC dam is studied using predefined block models from four sections of the dam (since dams are built in blocks): a block 11.75 meters long comprising a 3 meter thick stack from the spillway, a small block 8.75 m long from a typical full section, a block 24.40 m long from the tailrace and a block 40 m in length from the section equipped with intake to the powerhouse.
With the blocks and slabs, different cases of stability will be examined: when the water level in the reservoir is normal, at flood check conditions and at overflow conditions and the tailrace water level at different height will also be considered. The stability of the dam when the gates are opened and closed and the different efficiency or inefficiency of the drainage system will also be examined.
Historical experience shows that by far the most prevalent category of potential failure modes for a concrete dam are those related to loss of foundation support for the dam [2]. Significant loss for foundation support induces concrete stresses for which the dam was not designed. This can lead to cracking of the dam, and potentially its failure.
Sliding along weak discontinuities in the foundation rock is the most commonly encountered scenario related to this potential failure mode. Sliding is most likely to occur: (i) parallel to bedding planes or planes of schistocity , (ii) on low strength layers within the foundation (such as shale or bentonite seams ), (iii) at contacts between different rock units, or (iv) at other continuous ( or nearly continuous) planes of low shear strength in the foundation. For a block of rock to move, it must have “ release” planes on all sides. Such released planes typically are formed by jointing in the rock, possibly in combination with fault or shear zones. The presence of reservoir seepage water in the rock leads to lower effective normal stresses, and therefore lower frictional resistance, along the slide plane(s). The water can also, in some instances, result in shear strength loss in foundation materials.
Another potential scenario related to this failure mode is for structural distress to the dam to result from significant differential compressibility of rock units in the foundation, which were not accounted for in the dam design. Resulting differential movements in the dam could overstress the concrete, leading to cracking and potentially dam failure. This failure scenario is mainly relevant to dams where potential future loads imposed on the foundation rock may be significantly greater than loads experienced to date.
With a good understanding of the possible failure scenarios associated with this potential failure mode, the routine dam safety performance monitoring can be established.
We consider that the dam is made up of basically two types of materials (roller compacted concrete (RCC) and vibrated conventional concrete) having the following global characteristics:
Concrete cohesion between two levees 0KPa
Angle of friction in the Concrete 0KPa450
Density of reinforced concrete 0KPa 2.5
Density of RCC 0KPa2.3
The contact at concrete – rock has the following characteristics:
Cohesion in contact concrete-rock 0KPa 0KPa
Angle of friction at contact concrete – rock 0KPa450
When the drainage system is efficient [7], the distribution of pressure at the concrete –rock contact point is as indicated below;
The distance between the upstream face of the dam and the drainage curtain is 4 Meters. The uplift pressure on the right of the drainage curtain is Hus + (Hus – Hds)/3
Figure 1: Uplift pressure in contact concrete-rock with efficient drainage system (Trapezoidal uplift pressure pattern is broken)
If the drainage system is inefficient, a triangular distribution of the uplift pressure is envisaged.
Figure 2: Uplift pressure at contact concrete-rock with inefficient drainage system (Triangular uplift-pressure)
For the pressure in the levee of the RCC, we consider that the total upstream force is dissipated linearly between the upstream face of the dam and the drainage curtain that is, within the first 4 meters.
Figure 3: Uplift-pressure within the dam
Similarly, calculations were made taking into account the maximum probable seismic situation (MPS) characterized by a pseudo-static horizontal acceleration value of 0.1 g and a vertical acceleration equal to 50% of the MPS i.e. 0.05 g. As to what is considered as the behavior of the dam during seismic state, it is established that the inner pressures do not vary[3]. The duration of an oscillation is so short that the inner pressure does not have the time to change in one direction or the other.
The calculations have been made with the aid of software developed by the firm 'COYNE et BELIER'.
The method consists of calculating the forces applied on a horizontal section of a small piece of previously defined block (as well as the concrete – bedrock contact) and then deduce the following;
The mobilized sliding coefficient:
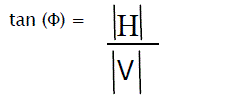Eq1
The Shear Friction Factor (SFF):
Eq2
The total effective forces
With:
H resultant horizontal forces (positive if directed downstream)
V resultant vertical forces (positive if directed upwards)
S surface section
c cohesion of partial friction at the bedrock – concrete contact point
Fc coefficient of partial safety for cohesion
Φ rock –concrete angle of friction at the contact point between concrete – bedrock
FΦ coefficient of partial safety for friction
The calculations have been done to get the effective force. It is a conservative choice which would help us get the lowest possible coefficient of security. The repartition of the forces in the different horizontal sections was also evaluated. For a linear repartition of the effective forces and a crack which is expanding (due to the existence of a zone under tension), the stabilized length of the crack is calculated.
The stability of the dam is calculated with respect to the forces of sliding, overturning and maximum admissible forces in compression and traction [4], [5].
Three cases of forces must be taken into account:
- Usual cases corresponding to cases of exploitation in which the forces do not produce any damage to the structure when in use.
- Rare cases corresponding to cases of forces under rare use but the installations must rest intact and function properly. Light disagreement and damage could be accepted on condition that they do not cause suspension of production.
- Extreme cases corresponding to cases of forces under critical conditions in which the installations can be damaged but not destroyed
The methods used are those of partial safety coefficients Fc and FΦ, applied respectively to tan (Φ) and c and the values are given on the table that follows:
Tabale 1: Safety Coefficients – Criteria for designing
The CSF is the coefficient of safety on the resistance to the compression of concrete.
Typical Sections:
The following sections have been studied:
The spillway for a block 11.75m long comprising a slab of 3m thick. The effects of the hydraulic force on the sluice gates attached to slab have been taken into account.
- A typical full section for a block 8.75m long
- The tailrace on a block of 24.4m long
- The section equipped with the intake on a block 40m long
Figure 4: Geometries of block sections studied
The results of the safety coefficient of the different cases treated are presented in the following tables.
Table 2: Safety coefficient – Block « From current section »
Table 3: Safety coefficient – Block « spillway »
Table 4: Safety coefficient – Block « Tailrace »
Table 5: Safety coefficient – Block « Intake »
The stability of the dam is therefore assured for all the cases of stability for different loads studied.
This is the seismic value for which the safety coefficient is equal to 1. The maximum seismic value for which the stability of the dam is assured corresponds to a horizontal acceleration 0.15 g and a vertical acceleration of 0.075 g.
The calculations presented here concern the stability to sliding and overturning of the supporting walls made of RCC situated on one part or the other of the RCC dam on which sedimentation occurs and thus presents a force on the wall.
The characteristics of concrete and of the foundation are identical to those described in the precedent section. The soil is considered at rest and as a result the push (thrust) coefficient of the soil is given by:
Eq3
With Φ = 45° being the angle of friction of the materials (rocks) constituting the sedimentation or transitional dike.
Once in water, we consider that the level of water is in one way or the other equal to the height of the supporting walls. The methods used in calculation are similar to those used above.
The section most badly placed in terms of load corresponds to a backfill height at an upstream elevation of h = 46m. The calculations were done on a block which has a thickness of 1m.
Figure 5: A typical section of the supporting wall
The 4 following cases have been envisaged:
- Case 1: End of construction (or empty reservoir): no water at the river bed and at the level of ground at altitude 677.55 Cameroon geographic level (CGL).
- Case 2: Reservoir at normal level: water level at 674.50 Cameroon geographic level and one part or the other of the dam with a full pressure on the dam and at the level of the ground at altitude 677.55 CGA.
- Case 3: End of construction (or empty reservoir) and maximum seismic state of project: 0.1 g from upstream towards downstream and 0.05 g of vertical acceleration.
- Case 4: Reservoir water at normal level and maximum project seismic state: 0.1 g from upstream towards downstream and 0.05 g of vertical acceleration.
The different safety coefficients calculated by STABCON are given in the table below.
Table 6: Safety coefficient - supporting wall
The stability of the structure is verified for each block of RCC dam even for the extreme cases of exploitation.
- In the 'normal' case the minimum criteria for stability to shearing are respected. The stability with respect to sliding and overturning is guaranteed no matter the level of water at upstream and downstream (normal reservoir or highest water level). For each and every geometric structure, no cracking is expected.
- In case of malfunctioning of the drainage system, the stability to shearing on the whole structure is again guaranteed. A slight crack at the level of the block (spillway) is expected at the level of the toe of the dam upstream. However this does not attain the drainage curtain.
- The stability is proven in case of seismic state for an upstream load corresponding to normal water level and for a horizontal acceleration equivalent to 0.1 g. The calculations also show that the criteria for stability are verified for a maximum acceleration of 0.15 g.