Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Analysis of IM Fed by Multi-Carrier SPWM and Low Switching Frequency Mixed CMLI

Srinivas Reddy Chalamalla1, S. Tara Kalyani2
  1. M.Tech, Department of EEE, JNTU, Hyderabad, Andhra Pradesh, India1
  2. Professor, Department of EEE, JNTU, Hyderabad, Andhra Pradesh, India2
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper presents analysis of induction motor fed by a Multi-carrier based sinusoidal pulse width modulation (SPWM) and a low frequency switching mixed cascaded multilevel inverter (MCMLI). A cascaded multilevel inverter using a single dc source and a capacitor is promising quality output waveform is known as mixed cascaded multilevel inverter (MCMLI) and its implementing with seven-level. Since the method using low frequency switching it has less switching losses and has high single stage output efficiency. Also the paper presents modelling and simulation of a Multi-carrier based SPWM Multilevel Inverter of high switching frequency, thereby showing the output comparison to MCMLI. Both test systems are modelled using MATLAB. In this work, SIMULINK is used and tested Induction Motor characteristics at different loads.

Keywords
Multi Level Inverter (MLI), Mixed Cascaded Multi Level Inverter (MCMLI), Total Harmonic Distortion (THD), Sinusoidal Pulse Width Modulation (SPWM), Induction Motor (IM).

INTRODUCTION
The Multilevel converters are mainly use to synthesize a designing of an single- or three-phase voltage waveform, many topologies are introduced in multilevel inverters like diode-clamped method, flying back capacitor, and cascaded structures method, are intensively studied for high-power applications because of its low electromagnetic interference and high efficiency, as in [1]-[6]. These inverters can solve the problems associated with existing 2-level inverters. Solar cells, fuel cells, batteries, and ultra-capacitor are the most common used independent sources, as in [3]. This structure can be considered in two arrangements, symmetrical and asymmetrical. The use of asymmetric input voltages can reduce, or when properly chosen, eliminate redundant output levels. In addition more different output voltage levels can be generated with the same number of components, compared to a symmetric multilevel inverter.
Traditionally, in each phase of a cascaded multilevel inverter requires n number of dc sources for 2n + 1 level. For many applications, obtaining so many separate dc sources may preclude the use of an inverter, as in [9]. The control aim of the MCMLI needs to maintain the balance of the dc voltage level of the capacitors while producing a nearly sinusoidal three-phase output voltage using a low frequency switching harmonic elimination method. This paper utilizing a method called the seven-level fundamental frequency harmonic elimination method to MCMLI.

PRINCIPLE OF HCMLI
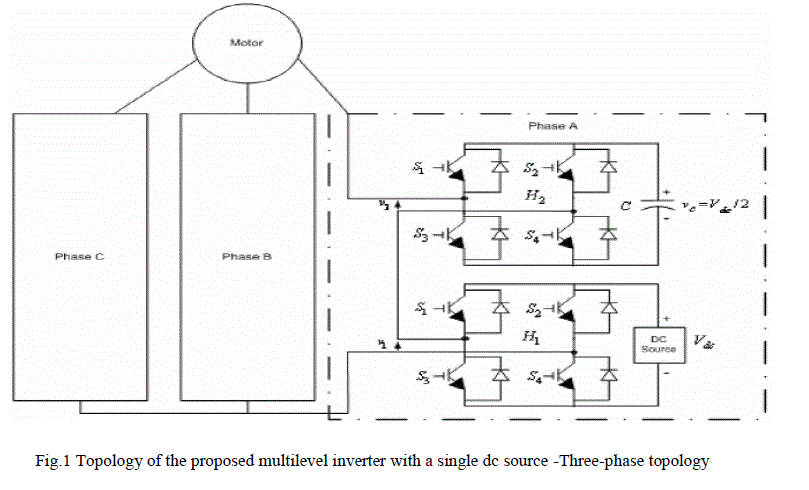
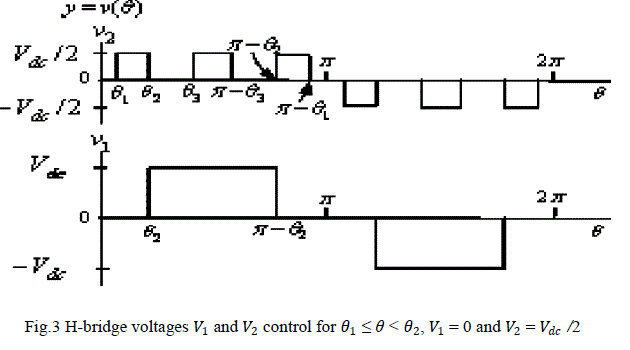
To operate a cascaded multilevel inverter using a single dc source, capacitors are used as the dc sources for all but the first source. To explain, consider a cascaded multilevel inverter with two blocks as shown in Fig. 1. The dc source for the first block is a battery or fuel cell with an output voltage of , while the dc source for the second block (H2) is a capacitor whose voltage is to be held at . The output voltage of the first block is denoted by 1 and the output of the second block is denoted by 2 so that the output voltage of the cascaded multilevel inverter is
V(t) = V1 (t) + V2> (t)
By opening and closing the switches of H1 appropriately, the output voltage;1 can be made equal to , 0, or while similarly the output voltage of H2 can be made equal to , 0, or by opening and closing its switches appropriately. Therefore, the output voltage of the inverter can have the values +, 0, , and utput levels, as in [9].
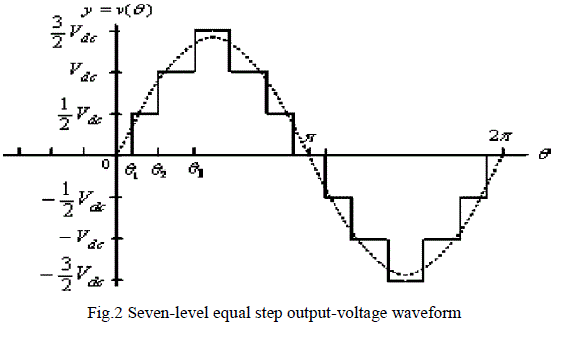
To balance the capacitor’s voltage, not all the possible voltage levels must be used in a cycle. A simple seven-level output voltage case, /2 can be designed, as shown in Fig. 2, when the capacitor block voltage V2 and dc source block voltage V1 are cascaded as shown in Fig. 3.
The Fourier series expansion of the seven-level equal step output voltage waveform shown in Fig. 2 is
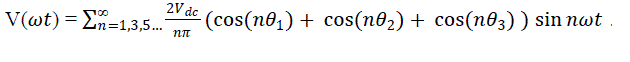image
Where n is the harmonic number of the output voltage of the multilevel inverter. Ideally, required fundamental component ??1. For three-phase inverter applications, the triplen harmonics in each phase need not be cancelled as they automatically cancel in the line-to-line voltages. The goal is to achieve the fundamental and eliminate the fifth and seventh harmonics. Using Eqn. (1), this can be formulated as the solution to the following equations:
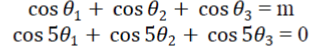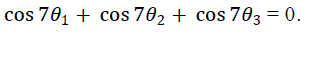image
image
Switching Angle Solution:
Eliminating the third, fifth and seventh harmonics and achieving required fundamental component V1 is done by calculating firing angles1, 2, 3 with the solution of Eqn. (2) and these angles lines between 0 to/2. Transcendental equations Eqn. (2) is converted into polynomials equations then solution of these polynomials gives the switching angle solution, is known as resultant theory. Since the output voltage follows the one fourth symmetry, other firing angles can be calculated with advancement of angle/2 and similarly after to .

MULTI-CARRIER BASED SPWM
There are two PWM methods mainly used in multilevel inverter control strategy. One is fundamental switching frequency and another one is high switching frequency. The MCMLI explained comes under fundamental switching frequency control strategy. In high switching frequency control among the available methods SPWM is the most used for the multilevel inverter, because it is very simple and easy to implement.
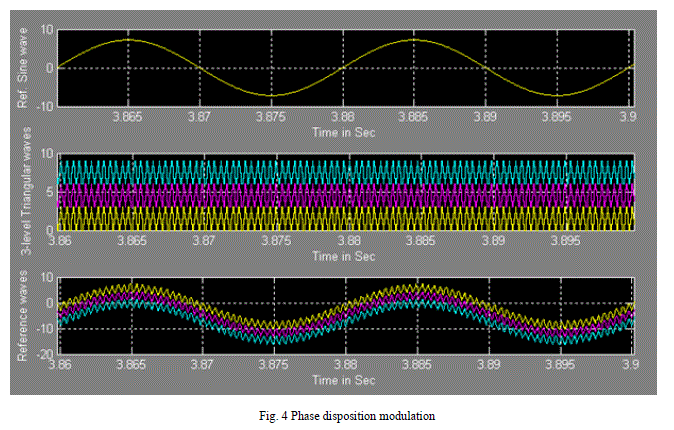
This work is done utilizing the simplicity of multi carrier sine PWM. For an n-level inverter, n-1 carriers with the same frequency fc and the same amplitude Ac are disposed such that the bands they occupy are contiguous. The reference waveform has maximum amplitude Am, a frequency fm, and its zero centered in the middle of the carrier set. The reference is continuously compared with each of the carrier signals. If the reference is greater than a carrier signal, then the GTO corresponding to that carrier is switched on and if the reference is less than a carrier signal, then the GTO corresponding to that carrier is switched off.
In multilevel inverters, the amplitude modulation index (ma) is the ratio of reference amplitude (Am) to carrier amplitude (Ac).
ma = Am / (m-1) Ac
The frequency ratio (mf) is ratio of carrier frequency (fc) to reference frequency (fm).
mf = fc / fm
A. Multi-Carrier Based SPWM MLI:
In phase disposition method all the carriers have the same frequency and amplitude. Moreover all the n-1 carriers are in phase with each other. It is based on a comparison of a sinusoidal reference waveform with vertically shifted carrier waveform as shown in Fig 4. This method uses n–1 carrier signals to generate n level inverter output voltage. All the carrier signals have the same amplitude, same frequency and are in phase. In this method three triangular carrier waves have compared with the one sinusoidal reference wave. A seven level cascaded H bridge multi level inverter is simulated in MATLAB / SIMULINK environment. The various method of the carrier based disposition analysis and gets the output waveform in a seven level inverter. SPWM generation circuit contains three carrier wave and one reference sine wave, then compared signal is given to the corresponds GTO to the multilevel inverter.
SPWM method is the extension of bi-level SPWM, one reference signal is used to compare to the carriers. 3 H-bridges being used for 7 level output voltage. This result has been obtained for the multi-cell converter in a sevenlevel configuration, which uses three series-connected cells in each phase. In 3-triangle method, therein, for 7-level inverter the A-phase duty cycle is compared with (3 in general) triangle waveforms.
B. Hybrid-Cascaded MLI connected to IM:
The modelled HCMLI and the firing angle results obtained from the resultant theory being used for obtaining 7-Level output voltage, Fig.7 is the SIMULIK model.
Same Induction Motor is being connected for characteristic analysis and Fig. 9 show the Speed, Torque and Current characteristics.
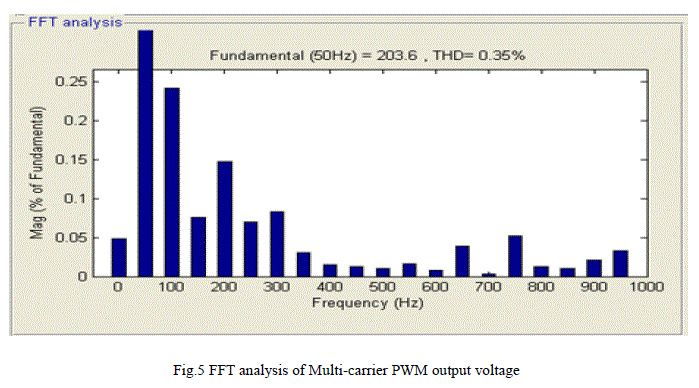
For modulation frequency 2500Hz results are obtained, compared to the HCMLI configuration Multi-carrier SPWM MLI has low THD but is operating at higher frequency which is resulting thermal stresses on device. As the switching frequency of modulating wave increases THD is reduced but thermal stresses increases. HCMLI is comparably operating at low that is at 50Hz is resulting nearly sinusoidal and had THD of 23%.
For the same IM and load characteristics with no filter circuits employed in the output stage of both inverter circuits HCMLI has 12% more currents in starting currents but has less current ripple than Multi-carrier based SPWM. Speed characterises are similar in both inverters. Torque and current ripple can be reduced using filter circuits. Since HCMLI working at low switching-frequency results high output efficiency and low thermal stresses in switching devices.

CONCLUSION
This paper utilizing a method called hybrid cascaded H-bridge multilevel Inverter (HCMLI) by implemented using a single dc power source and capacitors. HCMLI using one power source for each phase while producing desired 7-level multilevel voltage waveforms is performed. A fundamental frequency switching control algorithm is being used. This paper showing the difference and comparison between modeling and simulation of a Multi-carrier based SPWM Multilevel Inverter and Low Switching Frequency Hybrid Cascaded Multilevel Inverter fed to an Induction Motor and analysis of Induction Motor currents, torque and speed characteristics.

Tables at a glance
Table icon
Table 1
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
 

References