ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
| Jayaprakash J1, SenthilRajan T2, Harish Babu T3 Assistant Professor, Department of Instrumentation and Control Engineering, Sethu Institute of Technology, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Many application processes in industries typically requires control over at least two variables. This could use at least two control loops and makes it as multi-input multi-output (MIMO) or multivariable systems. Quadruple tank process (QTP) is one of the multivariable laboratory processes with four interconnected water tanks. This novel deals with mathematical modeling of the QTP by linearization principles and Jacobian matrix formation to represent the system in state space model. The linearized dynamics of the system have a multivariable zero that can be placed in both the left and right half of s-plane. The interaction between the control loops are studied using RGA and analyzed using LabVIEW. This process is ideal for illustrating multivariable control concept and also the performance limitations due to multivariable right half-plane zeros.
Keywords |
||||||||||||||||||||||||||||
| QTP, mathematical modeling, MIMO, State space model, Jacobian Matrix, Linearization. | ||||||||||||||||||||||||||||
INTRODUCTION |
||||||||||||||||||||||||||||
| A System may be classified into various types based on the inputs and outputs like SISO (Single input Single Output) and MIMO (Multi Input Multi Output). A SISO is a simple system with a single input and single output while MIMO system is a system with more than one input and outputs [1]. The QTP design is a well-known MIMO system suitable for analysis of various control schemes used in real-time which have nonlinear dynamics. Some systems cannot be represented by a linear model and require the use of nonlinear models. The nonlinearity in QTP is due to the square root term in mass flow relationship, between flow and level of the tank. The nonlinear models create more difficulty in optimizing the system and also its performance becomes poor. [6] The linearization of this type of system requires a stationary point around which the system operates. Taylor series expansion is one of the methods used for linearization which approximates the system at a given stationary point. Generally any system can be represented by state-space or Input-output model. Here it deals with the uses the former model where A, B, C and D of the state-space representation are obtained using Jacobian matrices. | ||||||||||||||||||||||||||||
| The stability of the nonlinear system can be analyzed by various methods like Lyapunov direct method, Popov criterion, method of linearization. It is possible to define the stability of the nonlinear system by also using the zeros by mapping them in real and imaginary axis known as Pole-Zero Map.Pole-Zero Map is a plot of the poles and zeros of a system model on the complex plane, where the real values are on the x-axis, and imaginary values are on the y-axis. | ||||||||||||||||||||||||||||
| Many real-time MIMO systems have interactions that occur due to inputs affecting more than one controlled variable. In QTP, a strong interaction exists between the tank 1 and tank 3 and also between tank 2 and tank 4. This happens due to input from pump 1 filling tank 1 and 3 along with output from tank 3 filling tank 1. Similarly interaction is present between tank 2 and tank 4. This interaction has adverse effect on effective control. The Relative Gain Array (RGA) is a measure of interaction between the control loops in multivariable control system [3]. | ||||||||||||||||||||||||||||
| When the MIMO system is such that each input only affects one particular output, different from the outputs affected by other inputs, the system is decoupled or non-interacting [8]. This novel deals with a real time implementation of Quadruple tank process which was modeled in two different approaches and analyzed the performance using MATLAB. | ||||||||||||||||||||||||||||
FOUR TANK PROCESS |
||||||||||||||||||||||||||||
| The Quadruple tank is a laboratory process with four interconnected tanks and two pumps as shown in Figure 1. The process inputs are u1 and u2(input voltages to pumps, 0-10V) and the outputs are y1 and y2 (voltages from level measurement devices 0-10V). The target is to control the level of the lower two tanks with inlet flow rates [9]. | ||||||||||||||||||||||||||||
| The output of each pump is split into two using a three-way valve. Pump 1 is shared by tank 1 and tank 3, while pump 2 is shared by tank 2 and tank 4. Thus each pump output goes to two tanks, one lower and another upper diagonal tank and the flow to these tanks are controlled by the position of the valve represented as γ. The position of the two valves determines whether the system is in the minimum phase or in the non-minimum phase. Let the parameter γ be determined by how the valves are set [3]. | ||||||||||||||||||||||||||||
| Each tank has a discharge valve at the bottom. The discharge from tank 4 goes to tank 1 while discharge of tank 3 goes to tank 2. This interaction creates a strong coupling between the tanks which makes it a multivariable control system. Due to its strong nonlinear behavior, the problem of identification and control of QTP is always a challenging task for control systems engineer.Discharge from tank1 and tank 2 goes to the reservoir tank at the bottom [2]. | ||||||||||||||||||||||||||||
MODEL DEVELOPMENT |
||||||||||||||||||||||||||||
| Modelling of a process is necessary to investigate how the behaviour of a process changes with time under influence of changes in the external disturbances and manipulated variables and to consequently design an appropriate controller [4]. This uses two different approaches, one is experimental and the other is theoretical. In such case a representation of the process is required in order to study its dynamic behaviour. This representation is usually given in terms of a set of mathematical equations whose solution gives the dynamic behaviour of the process. [10] | ||||||||||||||||||||||||||||
| For each tank i=1…4, the mathematical modelling is done by consideration of mass balance equation and Bernoulli’s law yields: | ||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||
| Before deriving the mathematical equations of the system lets consider, | ||||||||||||||||||||||||||||
| The input to the pump 1 be V1& for pump 2 be V2. | ||||||||||||||||||||||||||||
| The valve priority set for the flow is γ1γ2 [0, 1]. | ||||||||||||||||||||||||||||
| The flow through the pump 1 when V1voltage is applied is k1V1 and for pump 2 when V2 voltage is applied is k2V2. | ||||||||||||||||||||||||||||
| The flow through the pump is directly proportional to the input voltage applied for the pump. | ||||||||||||||||||||||||||||
| The flow in the tank 1 after crossing the valve 1 is γ1k1V1 and for tank 2 after crossing the valve 2 is γ2k2V2. | ||||||||||||||||||||||||||||
| The flow in the tank 4 after crossing the valve 1 is (1-γ1) k1V1 and for tank 3 after crossing the valve 2 is (1-γ2) k2V2. | ||||||||||||||||||||||||||||
| The non-linear model of the Quadruple tank process is given below. Mass balance equation states that | ||||||||||||||||||||||||||||
| [Rate of accumulation] = [Rate of in-flow] – [Rate of out-flow] | ||||||||||||||||||||||||||||
| Using the law of conservation of mass, | ||||||||||||||||||||||||||||
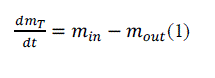 (1) (1) |
||||||||||||||||||||||||||||
| Where, mT= mass accumulated in the tank | ||||||||||||||||||||||||||||
| min= input mass flow rate | ||||||||||||||||||||||||||||
| mout= output mass flow rate | ||||||||||||||||||||||||||||
| Mass accumulated, mT= volume of tank (v) * density of liquid in the tank (ρ) | ||||||||||||||||||||||||||||
| Input mass flow rate (min) = volumetric flow rate (qin)* density of liquid in the inlet stream (ρ1) | ||||||||||||||||||||||||||||
| Output mass flow rate (mout) = volumetric flow rate (qout)* density of liquid in the outlet stream (ρ2) | ||||||||||||||||||||||||||||
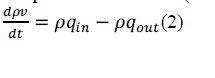 |
||||||||||||||||||||||||||||
| Since liquid using is same throughout the system, then ρ= ρ1 = ρ2. | ||||||||||||||||||||||||||||
| Modelling of non-linear Quadruple tank process is, | ||||||||||||||||||||||||||||
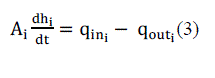 |
||||||||||||||||||||||||||||
| Where Ai denotes the cross sectional area of the tank, hi is the water level, is the in-flow of the tank and is out-flow of the tanki=1...4. | ||||||||||||||||||||||||||||
| The onlydepends on the input voltage supplied to the pump and the , depends on the acceleration due to gravity and the head of the water in the tank. The can be determined by the using Bernoulli’s equation and flow rate of the liquid. | ||||||||||||||||||||||||||||
| Therefore, | ||||||||||||||||||||||||||||
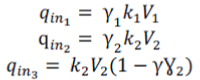 (4) (4) |
||||||||||||||||||||||||||||
| Where are the pumps constant, V1, V2 are the velocity of the flow of water through pump 1 and 2, γ1γ2are the valve ratio. | ||||||||||||||||||||||||||||
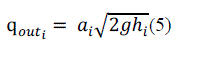 |
||||||||||||||||||||||||||||
| Where, | ||||||||||||||||||||||||||||
| ai = cross sectional area of the outlet pipes, g = acceleration due to gravity, hi = represents level of the water in each tanks i=1...4. | ||||||||||||||||||||||||||||
Tank 1 |
||||||||||||||||||||||||||||
| Using the law of conservation of mass, | ||||||||||||||||||||||||||||
| [Rate of accumulation] = [Rate of in-flow] – [Rate of out-flow] | ||||||||||||||||||||||||||||
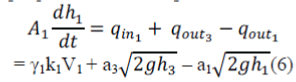 |
||||||||||||||||||||||||||||
Tank 2 |
||||||||||||||||||||||||||||
| Using the law of conservation of mass, | ||||||||||||||||||||||||||||
| [Rate of accumulation] = [Rate of in-flow] – [Rate of out-flow] | ||||||||||||||||||||||||||||
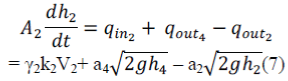 |
||||||||||||||||||||||||||||
Tank 3 |
||||||||||||||||||||||||||||
| Using the law of conservation of mass, | ||||||||||||||||||||||||||||
| [Rate of accumulation] = [Rate of in-flow] – [Rate of out-flow] | ||||||||||||||||||||||||||||
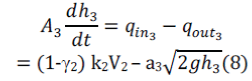 |
||||||||||||||||||||||||||||
Tank 4 |
||||||||||||||||||||||||||||
| Using the law of conservation of mass, | ||||||||||||||||||||||||||||
| [Rate of accumulation] = [Rate of in-flow] – [Rate of out-flow] | ||||||||||||||||||||||||||||
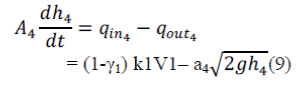 |
||||||||||||||||||||||||||||
| The Final equations, | ||||||||||||||||||||||||||||
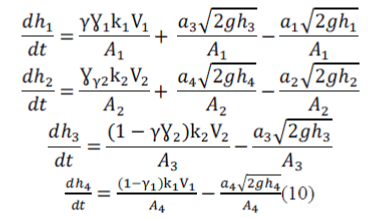 |
||||||||||||||||||||||||||||
| The above non-linear differential equation represents mathematical model of the four-tank system. The tank is being mathematically modelled by using law of conservation of mass. It is always enough to develop a controller for a particular process using its mathematical model. But here in QTP there is a challenge, that due to its non-linearity and uncertainty it is difficult to develop a controller which must take a proper control action [5]. | ||||||||||||||||||||||||||||
TAYLOR SERIES AND JACOBIAN CONVERSION |
||||||||||||||||||||||||||||
| The non-linear relationship in the equation (10) is due to the square root term present in those equations which makes the controller design difficult. To overcome the difficulty the linearization is required.The equation (10)issolved using Taylor series followed by Jacobian matrix transformation to obtain a state space form of the QTP. After obtaining the State space model of QTP the state space to transfer function conversion is done by using a simple conversion technique [13]. The initial step is to obtain a linear approximation of the differential equations which is done by Taylor series. | ||||||||||||||||||||||||||||
| If the mathematical model of QTP is being integrated to obtain h1, h2, h3 and h4it produces an infinite series of values [14]. It is common practice to approximate a function by using a finite number of terms of its Taylor series.The general form of differential equation can be represented by, | ||||||||||||||||||||||||||||
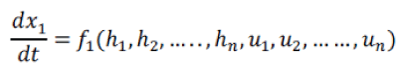 |
||||||||||||||||||||||||||||
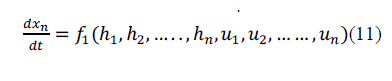 |
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
We use the Taylor series to yield the linear approximation. |
||||||||||||||||||||||||||||
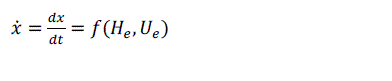 |
||||||||||||||||||||||||||||
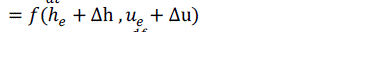 |
||||||||||||||||||||||||||||
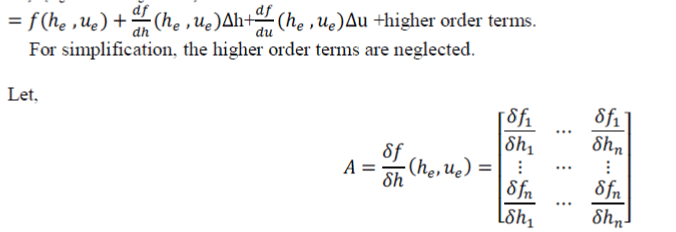 |
||||||||||||||||||||||||||||
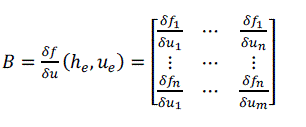 |
||||||||||||||||||||||||||||
| are the Jacobian matrices of with respect to h and u, evaluated at the equilibrium point,[ | ||||||||||||||||||||||||||||
| The Jacobian is used to solve systems of differential equations at an equilibrium point or approximate solutions near an equilibrium point. | ||||||||||||||||||||||||||||
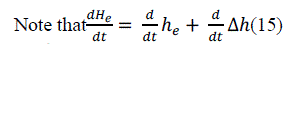 |
||||||||||||||||||||||||||||
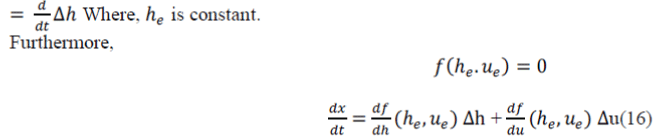 |
||||||||||||||||||||||||||||
| Let | ||||||||||||||||||||||||||||
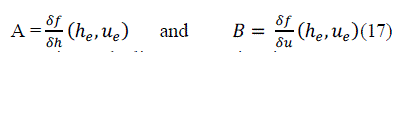 |
||||||||||||||||||||||||||||
| Neglecting the higher-order terms, we arrive at the linear approximation. | ||||||||||||||||||||||||||||
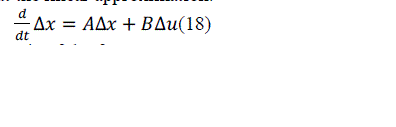 |
||||||||||||||||||||||||||||
| Similarly, if the outputs of the non-linear system is of the form, | ||||||||||||||||||||||||||||
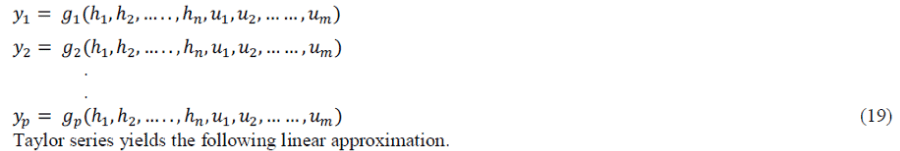 |
||||||||||||||||||||||||||||
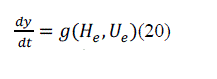 |
||||||||||||||||||||||||||||
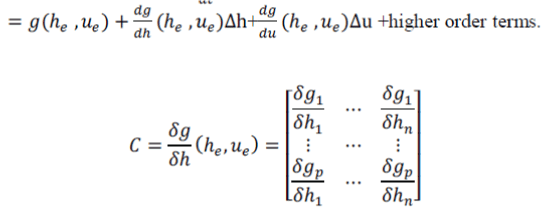 |
||||||||||||||||||||||||||||
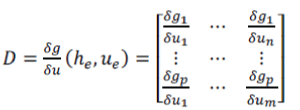 (21) (21) |
||||||||||||||||||||||||||||
| Neglecting the higher-order terms, we arrive at the linear approximation. | ||||||||||||||||||||||||||||
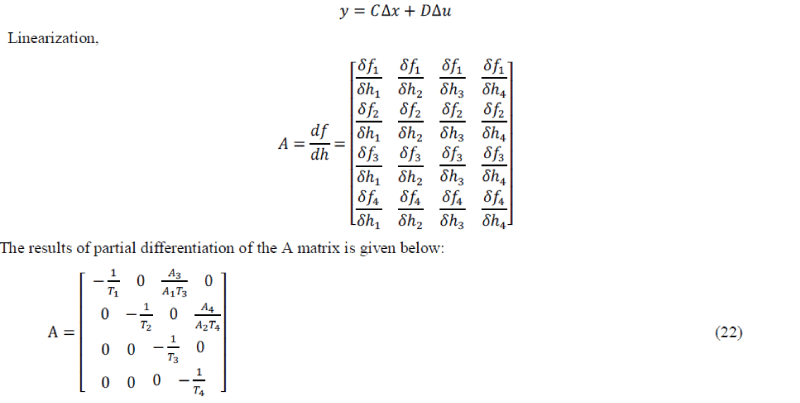 |
||||||||||||||||||||||||||||
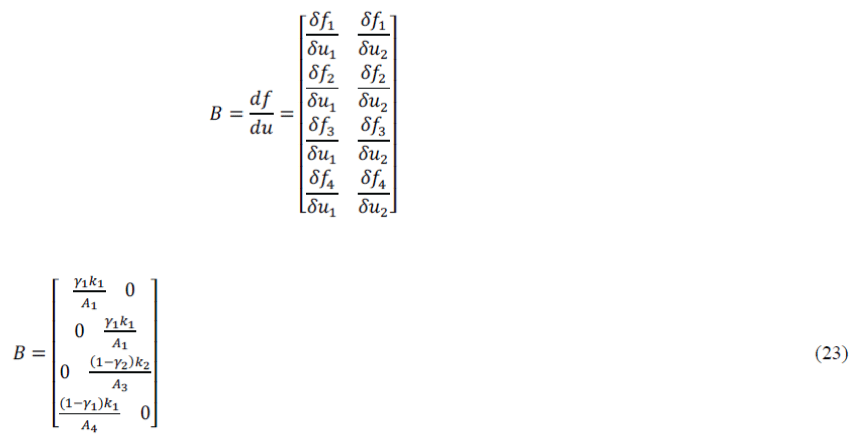 |
||||||||||||||||||||||||||||
| The output equations are, | ||||||||||||||||||||||||||||
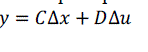 |
||||||||||||||||||||||||||||
| There are two outputs from the process. They are the level of the lower two tanks. | ||||||||||||||||||||||||||||
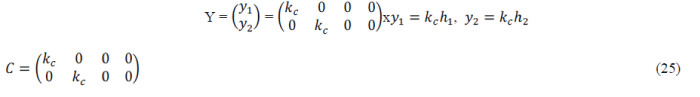 |
||||||||||||||||||||||||||||
| Actually the total output which is obtained from the system will be the levels of all the four tanks. And it is necessary that only the levels of the lower two tank is enough to be considered. | ||||||||||||||||||||||||||||
| State space method generates a matrix from the system differential equations by making each order of the derivatives into a variable.The state space representation serves as an alternative to transfer function representation of a system so that a SISO or a MIMO process can be treated equally. The state-space representation is best suited both for the theoretical treatment of control systems and for numerical calculations. The determination of the system response in the homogeneous case with the initial condition x (to) is very simple. For these many advantages the state space representation is carried out for the quadruple tank process. The linearized state space equation of a quadruple tank process is given as, | ||||||||||||||||||||||||||||
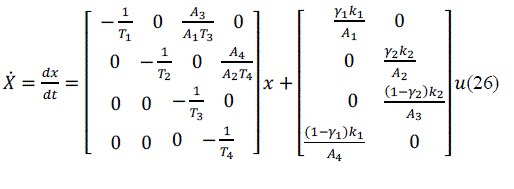 |
||||||||||||||||||||||||||||
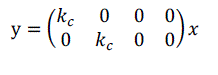 |
||||||||||||||||||||||||||||
| The equation (26) and (27) gives the state space analysis ofthe QTP which is obtained from the developed mathematical model. | ||||||||||||||||||||||||||||
TRANSFER FUNCTION MODEL |
||||||||||||||||||||||||||||
| The transfer function method applies a Laplace transformation to the differential equations, which allows handling them as a single algebraic equation [7].The key advantage of transfer functions is in their compactness, which makes them suitable for frequency-domain analysis and stability studies. However, the transfer function approach suffers from neglecting the initial conditions.To determine the transfer function for the QTP the following formula is used, | ||||||||||||||||||||||||||||
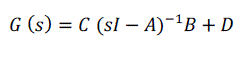 |
||||||||||||||||||||||||||||
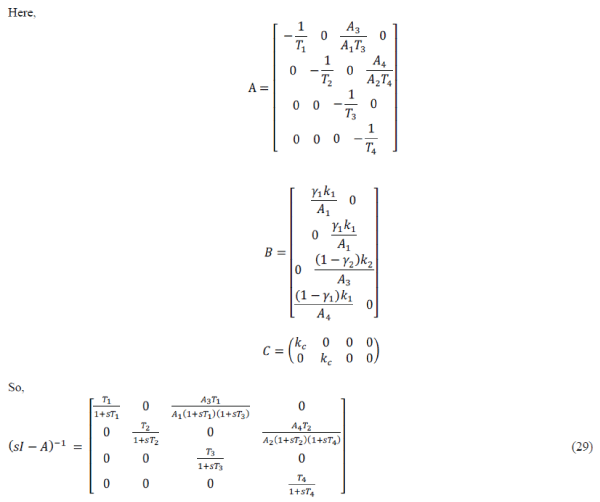
| Here, | ||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||
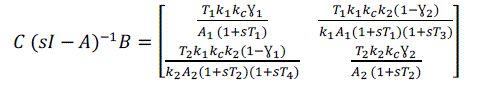 (30) (30) |
||||||||||||||||||||||||||||
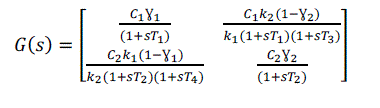 (31) (31) |
||||||||||||||||||||||||||||
| are approximately equal to 1. The corresponding transfer matrix is | ||||||||||||||||||||||||||||
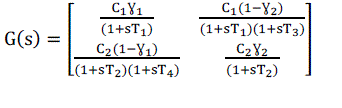 (32) (32) |
||||||||||||||||||||||||||||
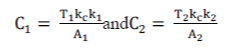 |
||||||||||||||||||||||||||||
| Thus the equation [32] shows the transfer function of QTP which has been derived from state space equation. | ||||||||||||||||||||||||||||
MINIMUMPHASE AND NON-MINIMUM PHASE |
||||||||||||||||||||||||||||
| The system is said to be in minimum phase or non-minimum phase based on the location of the multivariable zeros of G(s). These zeros are the zeros of the numerator polynomial given as follows: | ||||||||||||||||||||||||||||
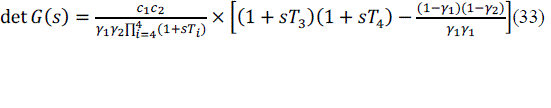 |
||||||||||||||||||||||||||||
| The system is found to be in non-minimum phase if | ||||||||||||||||||||||||||||
| And found to be in minimum phase if | ||||||||||||||||||||||||||||
| The figure 6 and 7 clearly shows the pole and zero map of the system when it is operated in minimum phase (i.e. + and non-minimum phase There is a pole shift to the right half of the s-plane when the system is operated in non-minimum phase. This causes the uncertainty of the process under study. | ||||||||||||||||||||||||||||
SIMULATION RESULT |
||||||||||||||||||||||||||||
| The result is obtained for the minimum phase and non-minimum phase operation of the quadruple tank process in both open loop and closed loop. The transfer function analysis and state space analysis are compared and the performance of the system is studied for the PI controller which is implemented. | ||||||||||||||||||||||||||||
| The figure 8 and 9 distinguishes the simulated output of the quadruple tank process in transfer function and state space analysis for the open loop operation. It is clear that the response obtained for the system is the tanks 1 and 2 takes short time to settle in transfer function model rather than the state space analysis of the system under study. | ||||||||||||||||||||||||||||
| The figure 10 and 11 shows the simulated output of the quadruple tank process in transfer function and state space analysis for the open loop operation in non-minimum phase. In figure 10 the tank 1 and 2 settles quickly and sharply at 10 and 12. And in the state space analysis the system takes much time of 200 sec to start to settle down. But the fact is, in state space analysis all the four tanks has given proper response in open loop operation. | ||||||||||||||||||||||||||||
| The figure 12 and 13 shows the simulated output of the quadruple tank process in transfer function and state space analysis for the closed loop PI controller operation in minimum phase. In figure 12 the tank 1 and 2 settles after it produce a small peak over shoot at 125 sec. In transfer function analysis the settling time takes 350 sec to settle down and has little oscillation. In the state space analysis the system produces a sharp peak over shoot at 75 sec and takes much lesser time of 135 sec to start to settle down. Here in figure 13 all the four tanks settles and response is good for the PI controller. The value of PI controller is chosen using the root locus technique.The minimum phase response for both the transfer function and state space analysis provides a better and satisfactory result. | ||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
| The simulated output of the quadruple tank process in transfer function and state space analysis for the closed loop PI controller operation in non-minimum phase shows thatthe tank 1 and 2 response is very poor as it never settles in non-minimum phase operation for PI controller. The Controller fails to take action and the performance of the controller is not satisfactory. Figure 14 clearly shows there is a strong interaction between the tanks. The impact of the interaction and uncertainty is being clearly stated from the obtained response of the tanks both in transfer function and state space analysis. When comparing both the response the state space analysis provides a better and clear representation that the system can be studied in detail and much more clearly in state space analysis. | ||||||||||||||||||||||||||||
CONCLUSION |
||||||||||||||||||||||||||||
| The state space method works better with complex time domain responses, while the transfer function method is a frequency domain model. The QTP is very well suited for demonstrating minimum phase and non-minimum phase system. The study of transfer function and state space representation of the QTP helps in attaining a clear idea of the how the zero location in multivariable control systems affects the performance and act as the limitation for the controller performance. This is ultimately due to the effects of coupling and strong interaction effect between the tanks when it if operated in non-minimum phase. The response obtained in state space representation is much better than the transfer function. | ||||||||||||||||||||||||||||
Figures at a glance |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
References |
||||||||||||||||||||||||||||
Volume 22, Issue 1, Jan. 2014. Issue 12, December 2013. August 2013. Applications, Volume 66- No.20, March 2013. Control System”, in IJSAA, Volume 2, Issue ICRAET12, May 2012. |