ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Archana Yadav1, Gaurav Bhardwaj2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
In this paper, a simple general yet realistic MOSFET model named nth power law MOSFET model for I-V characteristic of MOSFET in linear and saturation region is proposed. Model can express I-V characteristics of short channel MOSFET’S at least down to 0.12-μm channel length and resistance inserted MOSFET. The model evaluation time is about 1/3 of the evaluation time of the SPICE MOS LEVEL-1model. The model parameter extraction is done by solving single variable equations .solution can be done within a second, being different from the fitting procedure with expensive numerical iterations employed for the conventional models. Model plays a role of a bridge between a complicated MOSFET current characteristics and circuit behaviour in the deep sub -micrometer region.
Keywords |
||||||||
| MOSFET, Parameter Extraction, Sub-Micrometer. | ||||||||
INTRODUCTION |
||||||||
| Analytical I-V models are necessary for the design of integrated circuits. The analytical treatment of MOSFET circuit is primarily done by Shockley model but this model, is not so much accurate, because it shows negligible effect for velocity saturation carriers and short channel effect. There have been many attempts to accurately model the characteristics of these transistors, including complicated empirical models used for SPICE simulations. After that analytic treatment of MOSFET is done by various precise MOS model like, spice level3 model, BSIM, etc. But, some of these takes more time in evaluating model, some needs a special system with a hardware/software combination to extracting model parameters. Some of these need expensive numerical iteration procedure to extract model parameters and extracted model parameters are not able to give satisfactory results. However, to fill the gap between the Shockley and more precise model a new model, named as nth-power model, preserving high accuracy is introduced for circuit analysis. The nth-power model (Sakurai and Newton, 1990; Sakurai and Newton, 1991), which assumes a non-integer nth-power relation between current and voltage, is the best model to extract parameters. The nth-power law MOSFET model is an extension of alpha power law MOSFET model but much more accurate in linear and saturation region. | ||||||||
| Model parameter extraction is done by solving single variable equations and can be done with in second. An analytical treatment of circuit operation can be carried out by using this model, which helps to understand circuit behaviour in sub micrometer region. Here this model is not compared with the other precise model, but it is placed just above the Shockley model. | ||||||||
| The model is presented in Section II and the model parameter extraction procedure is described in Section III. Section IV is dedicated to the results when the model is implemented in spice and followed by conclusion in Section V. | ||||||||
MODEL DESCRIPTION |
||||||||
| The proposed model equations are as follows. ID is the drain current | ||||||||
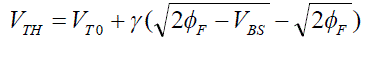 (1) (1) |
||||||||
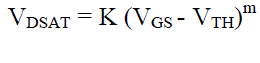 (2) (2) |
||||||||
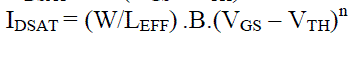 (3) (3) |
||||||||
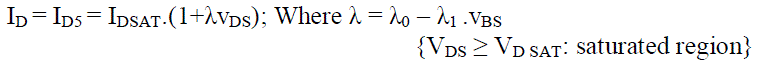 (4) (4) |
||||||||
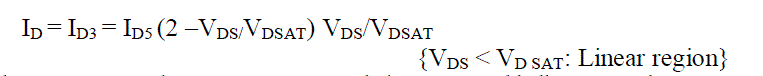 (5) (5) |
||||||||
| Where VGS, VDS and VBS are gate-source, drain-source, and bulk-source voltages, respectively. W is a channel width and LEFF is an effective channel length. VTH denotes a threshold voltage, VDSAT a drain saturation voltage, and IDSAT, drain saturation current. VT0, γ, and 2?F are parameters which describe the threshold voltage. Parameters K and m control the linear region characteristics while B and n determine the saturated region characteristics. λ0 and λl are related to the finite drain conductance in the saturated region. The subscript 3 and 5 for ID denotes a triode and a pentode operating region, respectively, and they are totally different from ID,3 and ID,5. | ||||||||
EXTRACTION PROCEDURE |
||||||||
| Select points 1 to 7 in I-V characteristics suitably as shown in below figure1 from[1] ,then we have ID,1- ID,7 , VDS,1- VDS,7 and VGS,1- VGS,7 . | ||||||||
| Now, we can find the parameters value by the formulas as given below:- | ||||||||
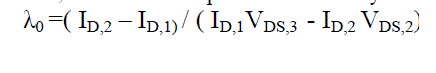 |
||||||||
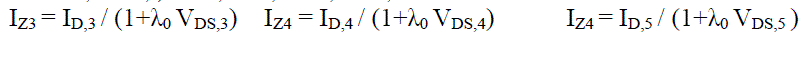 |
||||||||
| Then, VT0 can be obtained by solving the following equation. The bisection method is the best choice for the solution since it finds out the root without fail within ten iterations. | ||||||||
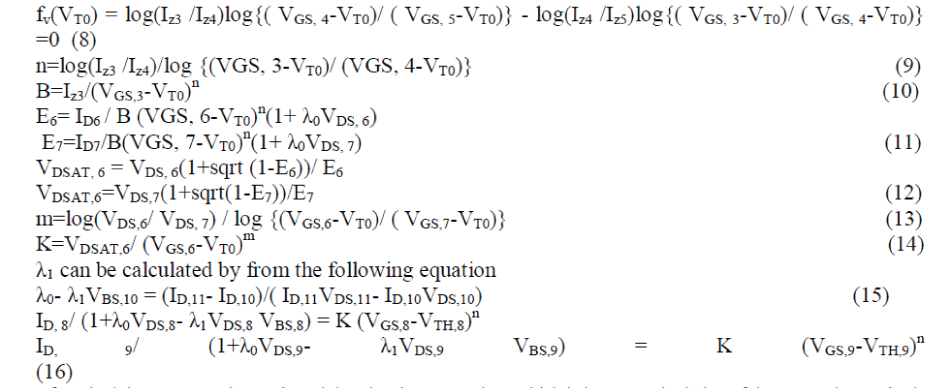 |
||||||||
| After obtaining VTH, 8, and VTH,9 by solving the above equations which is just a manipulation of the expressions, 2?F is obtained by solving the following equation with the bisection method:- | ||||||||
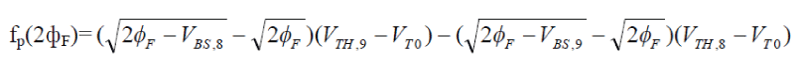 |
||||||||
APPLICATION OF MODEL FOR A MOSFET |
||||||||
| Now, we test this model by applying it to our calculated data for a MOSFET. But, we have limitation of sweeping only to voltages, so we cannot use different VBS values, i.e. we cannot calculate λ1, γ, and 2?. | ||||||||
| Circuit diagram:- | ||||||||
| In fig.1 a circuit diagram has been shown for output characteristics of MOSFET. Using LT- SPICE, a SPICE level 1 model has been used for output characteristics and voltage parameter is used as shown in diagram. | ||||||||
EXPERIMENTAL Ids Vs Vds:- |
||||||||
| In fig.2 we are sweeping Vgs from 0-5v and Vds from 0-5v and I-V characteristics are shown in fig. For different values of Vgs(1,2,3,4,5v). | ||||||||
| Parameters are extracted Choosing appropriate values on the above I-V and calculated values are mentioned below:- | ||||||||
| n =1.98 | ||||||||
| B =.0664 | ||||||||
| K =1.46 | ||||||||
| Using these parameters the graph has been modelled as shown in fig.3. | ||||||||
| I-V characteristics of MOSFET using this model | ||||||||
COMPARISON |
||||||||
CONCLUSION |
||||||||
| The proposed paper shows the implementation of nth power low MOSFET Model. It takes very less time for calculating the parameters because of the simplicity of model with linear equations. It is well suited for analytical treatment of circuit behaviour. This model is not to competing with the existing more precise models but can be used to provide a simple model which is placed just above the Shockley model. Using 3rd generation model we can achieve better results as comparison to 1st and 2nd generation models. | ||||||||
Tables at a glance |
||||||||
|
|
||||||||
|
||||||||
References |
||||||||
|