Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

“Ancient Indian Vedic Mathematics Based Multiplier Design for High Speed and Low Power Processor”

Mr. Nishant G. Deshpande1, Prof. Rashmi Mahajan2
  1. PG Student [VLSI &EMBEDDED SYS], Dept. Of ECE, Dr. D. Y. Patil S. O. E. ,Lohegaon ,Pune, Maharashtra, India
  2. Professor, Dept. of ECE, Dr. D. Y. Patil S. O. E. Lohegaon, Pune, Maharashtra, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The use of Vedic mathematics lies in the fact that it reduces the typical calculation in the conventional mathematics to very simple once. This is so because the Vedic formulae have claimed to be building on the natural principles on which the human mind works. Vedic mathematics is a several effective algorithms, which has spread over to various branches of engineering such as computing.. In this work, I have studied different multipliers, which give low power requirement and high speed, also give information of “urdhva-Tiryabhyam” algorithm of ancient Indian Vedic mathematics, which has utilized for multiplication to improve speed, area parameters of multipliers. . In this paper Urdhva-Tiryakbhyam sutra has been implemented with Xilinx (VHDL) and results are presented. This has improved speed of multipliers. After implementing the sutra with 8-bit it has been observed that Vedic multiplication is efficient in terms of speed.

Keywords
Vedic Mathematics, Multiplier, Urdhva-Tiryabhyam sutra, Nikhilam sutra

INTRODUCTION
Vedic mathematics is ancient methodology of Indian mathematics which has distinctive technique of arithmetic computation based on 16 sutras [1].
Vedic mathematics is extract from four Vedas (book of civil engineering and architecture), which is upya-veda (supplement) of artharva Veda. Owing to its simplicity and regularity, it finds its utility and applications in the field of geometry, trigonometry, quadratic equation, factorization and calculus. His holiness Jagadguru Shnkaracharya Bharti Krishna Tirthaji Maharaja (1884-1960) comprised all this work. He did extensive research in the Vedas and came up with the simplified form of calculation, which is yet powerful. He came up with the complete explanations and presented them in the form of sutras. He constructed 16 sutras (formulae) and 16 Upya sutras (sub formulae) after extensive research in Atharva Veda. As all these sutras has extracted from swamiji’s own finding and research, these have not found explicitly in Veda. ‘Vedic’ is term derived from the word ‘Veda’, which means storehouse of all knowledge. Vedic mathematics logics and steps have applied to problem involving trigonometric functions, Plane and sphere geometry, applied mathematics conics, differential calculus and integral calculus and of different kind. This has attributed to fact that the Vedic formulae have claimed to be building on natural principles on which human mind works. Thus, this shows some efficient algorithms, which can apply to various branches of applied science [2].
Multiplier is essential component of computer system, cellular phones and most audio/videos. The important functions implementation multiplier are Inverse Discrete cosine transform (IDCT), Fast Fourier transform (FFT), and multiply Accumulate (MAC). The known method of multiplication in coprocessor is array multiplication, booth multiplication each with its own multiplication. The array multiplier performs parallel multiplication. The parallel multiplication process has depended on the fact that in multiplication partial product can be separately compute in parallel. Array multiplier is the fast multiplication of two numbers since the delay it takes, is the time for the signal to propagate through the gates that form multiplication array. Booth multiplier is another significant method of multiplication. Highspeed multiplication and exponential operations require large booth adder arrays having large partial sum and partial carry registers [3].
The work presents multiplier architecture based on the ancient Indian Vedic mathematics sutra (formula) called Urdhva-Tiryabhyam (Vertically and crosswise) which has traditionally used for decimal system in ancient India. Some architecture based on Vedic mathematics based on decomposition has proposed that was better than traditional multipliers. The processor basically works in following ways, the grouping of bits 4 at a time is done both for the multiplicand and multiplier and thereafter the algorithm of Vedic Mathematics called Urdhva Tiryabhyam (Vertically and crosswise) is called to give the efficient multiplier architecture and increase the speed of multiplication and reduce the time delay [4].
This paper describes the design and implementation of 4×4 bit Vedic multiplier based on urdhva-Tiryabhyam sutra (Vertically and crosswise technique) of Vedic mathematics using EDA (Electronic Design Automation) tool. Section 2 describes the basic methodology of Vedic Multiplication technique. Section 3 describes the hardware architecture of 2×2 and 4×4 bits Vedic Multiplier (VM) based on Vedic multiplication [5].
The Nikhilam Navatascaram Dasatah exactly means “All from nine and very last from ten”. A sutra means start beginning the left most digit and begin subtracting from each of the digit; but subtract_10 from the very last digit. The following example illustrates the means in which this Sutra could reduce the number of iteration to reduce the whole Multiplication [6].
We write multiplier and the multiplicand in two rows followed by the differences of each of them from the chosen base, i.e., their compliments. We be able to now write two columns of numbers, one consisting of the number to be multiplied (column 1) and the other consisting of their compliments (column 2). The product also consists of two parts. The right hand side (RHS) of the product can be obtaining by simply multiplying the numbers of the columns 2. The left hand side (LHS) of the product have found by cross subtracting the second number of column 2 from the first number of Column 1 or vice versa. The results have obtained by concatenating RHS and LHS [7].

RELATED WORK
A multiplier is one of the key hardware blocks in most digital signal processing system, like frequency domain filtering (FIR and IIR), Correlation, Digital Image Processing etc. The implementation methodology ensure substantial reduction of propagation delay in comparison with Wallace Tree (WTM), modified Booth Algorithm (MBA), Baugh Wooly (BWM) and Row bypassing and Parallel Architecture (RBPA) based implementation which are most commonly used architecture. The architecture offered 29%, 31%, 35%, and 23% improvement in terms of propagation delay compared with WTM, MBA, BWM and RBPA based implementation respectively [1].
The architecture of Multipliers has generally classified into three categories. First is the “serial multiplier” which emphasizes on hardware optimization of chip area. Second is “parallel multiplier” which performs high-speed mathematical operations, the drawback being relatively larger chip area consumption. The final one is “serial-parallel multiplier” which is a trade-off between time-consuming serial multipliers and the area consuming parallel multiplier [2].
The proposed Vedic parallel overlay architecture can be of great significance when implemented with 4×4 high speed multipliers. The proposed architecture has the advantage that as the number of bits increases its gate delay and area increases very slowly as compared to other multiplier architecture. It has estimated that this design is quite efficient in terms of silicon area/speed [3].
The proposed multiplication were implemented using two different techniques namely conventional shifting & adding operation and Vedic technique for 4,8,16, 32 bit multipliers. It is evident that there is a considerable increase in speed of the Vedic architecture. The simulation outcome for 8, 16, and 32-bit multipliers has presented [4].
Reducing the time delay is very essential requirement for many applications and Vedic Multiplication technique is very much suitable for this purpose. The idea proposed here may set path for future research in this direction [5]. In this paper, we have presented a 4×4 architecture applying the Nikhilam Algorithm, the two inputs a and b represents the 4 bit multiplier and 4 bit multiplicand shown [6].
This paper describes the different techniques used in Ancient Vedic mathematics for multiplication and compares them [7].
Ancient Indian Mathematics gives efficient algorithms of formulae for multiplication, which increase the speed of device shown in [8].
The demand for high speed processing has been increasing because of expanding computer and signal processing application. Higher throughput arithmetic operations are important achieve the desired performance in many real time application unlike image and signal processing. One of the key arithmetic operations in such applications is multiplication and the development of fast multiplier circuit has been a subject of interest over decades [9].
Reducing the delay and power consumption is very essential requirement for much application. The work presents different multiplier architecture. Multiplier based on Vedic Mathematics is one of the fast and low power multiplier, which also minimizing power utilization for digital systems involves optimization at all levels of the design [10]

VEDIC MULTIPLICATION TECHNIQUE
The use of Vedic mathematics lies in the fact that it reduces the typical calculations in conventional mathematics to very simple one. This is so because the Vedic formulae have based on the natural principles on which the persons mind works. Vedic mathematics is methodology of arithmetic policy that allows more efficient speed performance. It also provides some efficient algorithms, which has applied to various branches of engineering such as computing.

Urdhva-tiryakbhyam sutra
Multiplication has based on an algorithm called Urdhva-Tiryakbhyam (Vertical & Crosswise) of ancient Indian Vedic Mathematics. UrdhvaTiryakbhyam Sutra is a general multiplication formula applicable to all cases of multiplication. The Sanskrit term means “Vertically and crosswise”. The thought here is to begin concept, which results in the generation of all partial products along with the concurrent addition of these partial products in parallel. Since there is a parallel generation of the partial products and their sums, the processor is liberating of the clock frequency. Thus, the multiplier will require the same amount of time to calculate the product and hence is independent of the clock frequency. The advantage here is that parallelism reduces the need of processors to operate at increasingly high clock frequencies. A higher clock frequency will result in increased power of processor and its disadvantage is that it will lead to increased power dissipation resulting in higher device operating temperatures. By occupying the Vedic multiplier, the entire demerits associated with the increase in power dissipation can be bargain. Since it is quite faster and efficient its layout has a quite regular structure. Owing to its regular structure, its layout has done easily on a silicon chip. The Vedic multiplier has the advantage that as the number of bits, increases also gate delay and gate area increases very slowly as compared to other multipliers, thereby making it time, space and power efficient [4]
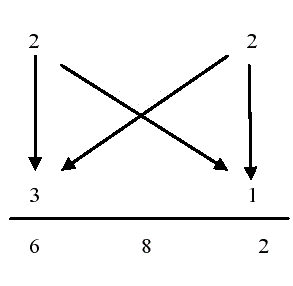
To illustrate this multiplication method, consider the multiplication of two decimal numbers (22 * 31). Line diagram for the multiplication has shown in Figure 1. This shows result 682. Firstly, the LSB digits on the both sides of the line has multiplied and added with the carry from the earlier step. This will produce one of the bits of the product and a carry. This carry have added in the next step and the process goes on likewise. If there is more than one line in onestep, all the results have added to the earlier carry. In each step, least essential bit act as the result digit and all other digits act as carry for the next step. Initially the carry has taken to be zero.

Block Diagram For 2×2 bit Multiplier
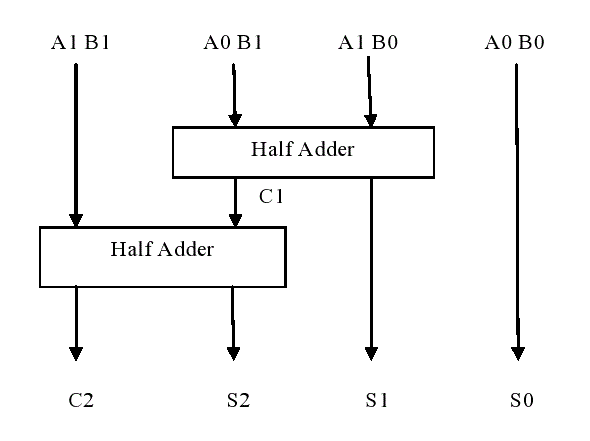
The 2x2 bit Vedic multiplier module is implemented using two half-adders & four input AND gates, which displays in its block diagram in Figure 2. Here A0A1 and B0B1 are multiplicand and multiplier respectively, S0S1S2C2 is product. We can extend the similar method for higher number of input bits. However, a little modification is required.

Proposed Multiplication
Initially, least significant bits are multiplied which gives the least significant bit of the product (vertical). Then, the LSB of the multiplicand has multiplied with the next higher bit of the multiplier and added with the product of LSB of multiplier and next higher bit of the multiplicand (crosswise). The sum gives second bit of the product and the carry has added in the output of next stage sum obtained by the crosswise and vertical multiplication and addition of three bits of the two numbers from least significant position, which displays in figure 3.
For 2-bit multiplication the inputs are multiplicand A=A1 A0 and multiplier B= B1 B0 and if S be the result then S3S2S1S0 is the product. Similarly, we can get results of 4-bit and 8- bit multiplication. Surely, the result obtained after 4×4 and 8×8 bit multiplication will be 8 and 16 bit respectively.

RESULTS AND DISCUSSION
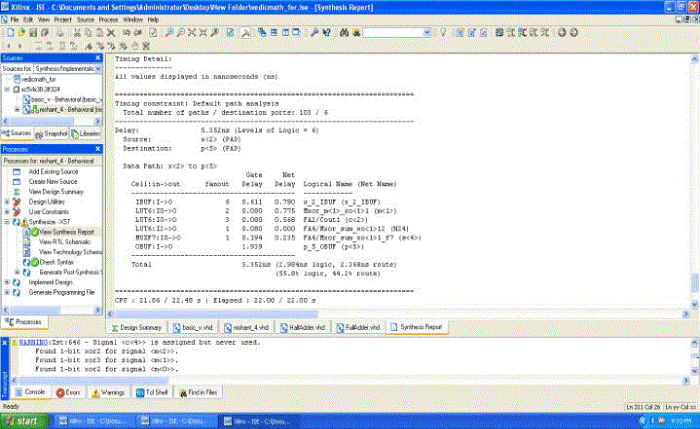
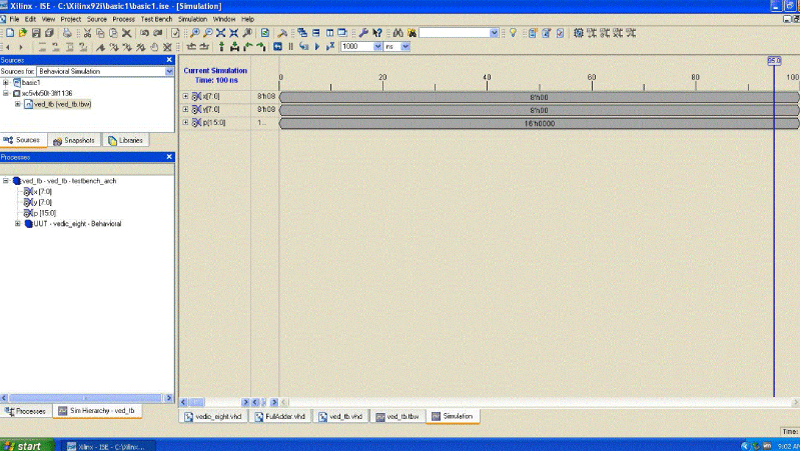
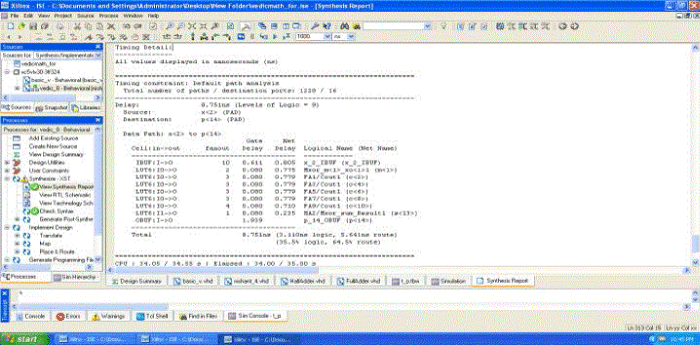
The time taken for multiplication operation has reduced by employing the Vedic algorithms. The proposed Vedic multiplier architecture exhibits speed improvements. The computational path delay for 4-bit and 8-bit Vedic multiplier is 5.352 ns and 8.751 ns. Corresponding results of simulation and synthesis have shown below

Simulation and Synthesis results for 4-bit Vedic multiplier
Synthesis result shows that for 4-bit multiplication maximum combinational path delay 5.352 ns.

Simulation and Synthesis results of 8-bit Vedic multiplier
Synthesis result shows that for 8-bit multiplication maximum combinational path delay 8.751 ns.
Synthesis and simulation result shows that time required to compute the result is very less as compared to Array and Booth multiplier.

CONCLUSION AND FUTURE SCOPE
Vedic multipliers are much faster than the conventional multipliers. Therefore, the design complexity has reduced for inputs of large no of bits and modularity is increased. Urdhva-tiryakbhyam is such algorithm, which can increase speed and ultimately reduce the delay, power requirement and hardware requirements for multiplication of numbers. The high-speed multiplier algorithm can enhance efficiency in terms of speed.
Depending on the inputs, the better sutra has selected by the architecture itself. Future work includes the integration of the divider block, multiply and accumulate (MAC) unit, thereby making it into a Vedic Arithmetic and Logical unit (ALU). Reducing the time delay is very essential requirement for many applications and Vedic Multiplication technique is very much suitable for this purpose. The idea proposed here may set path for future research in this direction.

ACKNOWLEDGMENT
I acknowledge with gratefulness and humanity my gratitude to Mrs. Rashmi Mahajan, Professor of Electronics and Telecommunication Department, Dr. D. Y. Patil S. O. E. Lohegaon, Pune, Maharashtra, India, for her guidance and support.
 

Tables at a glance
Table icon
Table 1
 

Figures at a glance


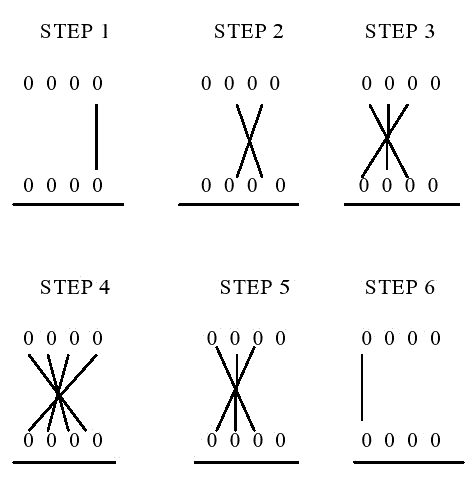Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
Figure 5 Figure 6 Figure 7
Figure 5 Figure 6 Figure 7
 

References