International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Apodised optical systems in resolving two point objects with shrink apertures

B. Sambaiah1 and D. Karuna Sagar2
  1. Research Scholar, Department of Physics, Nizam College, O. U., Hyderabad – 500 007, India1
  2. Professor, Department of Physics, Nizam College, (O.U.), Hyderabad – 500 001, India2
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

The influence of apodisation on the resolution of two point objects in the case of shrink apertures of rotationally symmetric optical systems has been studied by applying the modified Sparrow criterion introduced by Asakura to suit the case of unequally bright object points. The results are presented in terms of Rayleigh and Sparrow limits obtained for coherent, partially coherent and incoherent illuminations. It is found that shaping of the aperture along with the chosen Hanning amplitude filter is effective in increasing the resolving power of the optical imaging systems.

Keywords
Rotationally Symmetric Systems, Shrink aperture, Hanning amplitude filters.

INTRODUCTION
Two-point resolution studies forms an interesting area when the two point objects are situated within a close neighborhood of each other. The resolution necessary to satisfy astrophysical observations requires large-diameter optical systems. However, the size required for high-resolution optical systems is not practical in implementation. A shrink aperture system is composed to assess the performance of optical imaging systems in judging depending upon its ability in resolving closely situated object points. There are a number of quality criteria in the field of image science; two-point resolution criterion is one of the most important and most basic measures proposed for judging the quality of optical imaging systems [1]. Rayleigh [2] criterion states that the two point sources are just resolved if the central maximum of one falls on the first minimum of central maxima produced by the other point source. Sparrow [3] proposed an alternative criterion according to which the two points are just resolved if the second derivative of the resultant image intensity distribution vanishes at the point midway between the respective Gaussian image points. Asakura [4] has modified the Sparrow criterion to be applicable for the more realistic case of unequally bright object points. In the present study this modified Sparrow criterion has been applied to optical imaging systems apodised by the first order Hanning amplitude filters.

II. THEORY
The theoretical expression as given by Hopkins and Barham [5], for the total image intensity distribution in the image plane of an optical system, as a function of the reduced co-ordinate Z, is given by,
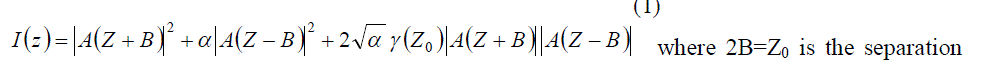image
over the exit pupil. Thereby, for  = 0 the filter function becomes an Airy pupil. Φd if the defocus parameter. For chosen apodizer the amplitude transmittance decreases monotonically from the center towards the edges of the pupil. Higher spatial frequency components of the object are diffracted by a larger angle and hence these go predominantly through the edge of the aperture. As the pupil transmittance is decreased at the edges as compared to that of the center, which results in the reduction in the higher spatial frequency components in the image. This manifests as partial or complete suppression of the undesired optical side lobes, which consequently enhances imaging characteristics. However, for shrink apertures the expressions for the amplitude PSF can be expressed as
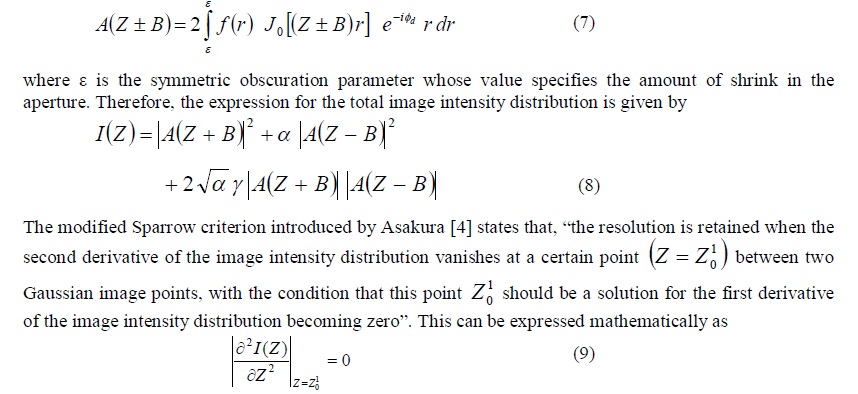image

III. RESULTS AND INTERPRETATIONS
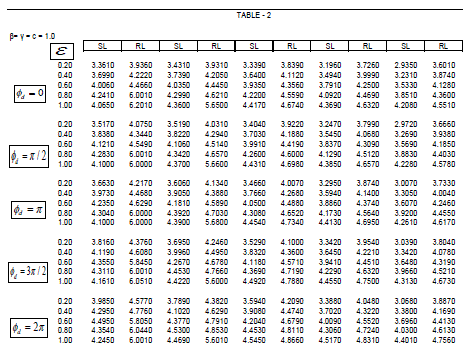
Expressions (8) and (9) have been used to compute the image intensity distribution of the two point objects and the Sparrow and Rayleigh limits of the optical systems with circular and shrink apertures apodised with the chosen amplitude filter. The results have been compared with that of the Airy case. Table-1 gives the computed values of Sparrow and Rayleigh limits (SL & RL) for clear aperture (β = 0), for various degrees of defect-of-focus when the optical imaging system is illuminated with coherent light and the two object points are of equal intensities (c = 1). With shrink aperture (ε ≠1) the sparrow limit as well as the Rayleigh limits decreases with decrease in the value of ε, thereby enhancing the resolving power of the optical system. This feature is observed for various defocused planes.
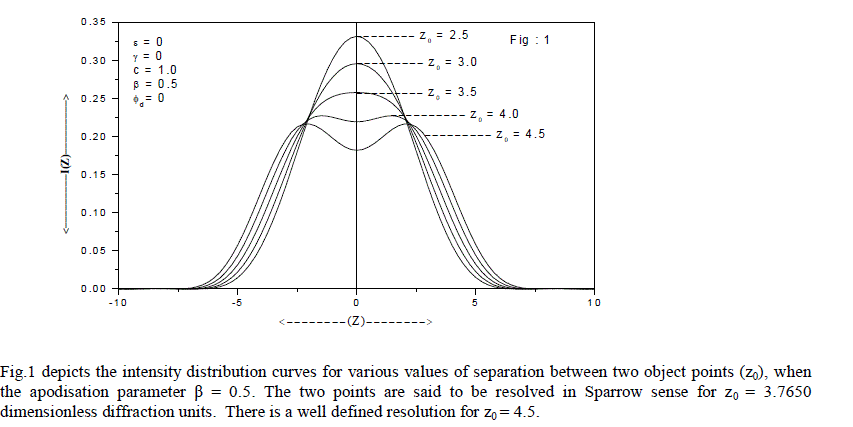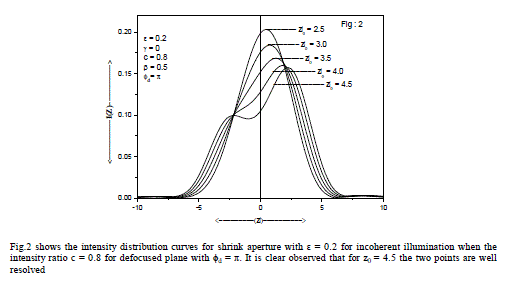
image
Fig.2 shows the intensity distribution curves for shrink aperture with ε = 0.2 for incoherent illumination when the intensity ratio c = 0.8 for defocused plane with ϕd = π. It is clear observed that for z0 = 4.5 the two points are well resolved. Table-2 provides the computed values of Sparrow and Rayleigh limits (SL & RL) for highly apodised aperture (β = 1), for various degrees of defect-of-focus when the optical imaging system is illuminated with coherent light and the two object points are of equal intensities (c = 1). With shrink aperture (ε ≠1)
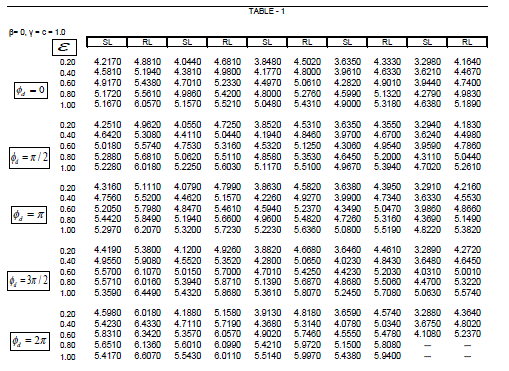image
the sparrow limit as well as the Rayleigh limits decreases with decrease in the value of ε. On comparing the tabulated values from both the tables 1 & 2, it can be concluded that with apodisation the resolution limit decreases thereby enhancing the resolving power of the optical system.
image
image
image

III. CONCLUSIONS
The process of apodising the optical system with Hanning amplitude filter, suppresses fully or partially the optical side-lobes of the individual point spread functions. The apodisation parameter is effective in shaping the point spread function so that there is an improvement of resolution of two point objects rendering the optical system to be more effective in their resolution.. Hence, the Hanning amplitude filters are effective in enhancing the resoling power of the given optical imaging system.

References
  1. K.Surendar, Ph.D. Thesis, Osmania University, Hyderabad, India, 1993.
  2. T.R.Corle and G.S.Kino, “Confocal scanning Optical Microscopy and Related Imaging Systems”, Academic Press, San Diego, 1996.
  3. A.Boiivin, “Theorie et calcul des Figures de Diffraction de Revolution”, Gauthier villars, Paris, 1964.
  4. Jacquint P and Roizen-Dossier B 1964 Progress in Optics ed. E. Wolf (North-Holland Publishing Company, Amsterdam) Vol III, Chapter 2.
  5. G.O. Reynolds, J.B. Develis, G.B. Jr. Parrent, and B.J. Thompson, “The New Physical Optics
  6. Notebook: Tutorial in Fourier Optics” IInd Ed., 38, 101 & 102, SPIE and American Institute of Physics, New York, U.S, 1990.
  7. J. P. Mills and B. J. Thompson, J. Opt. Soc. Am. (A), 3 (1986) 704.
  8. T. Asakura, Nouv Rev Optique. 5 (1974) 169.
  9. H.H. Hopkins and P.M. Barham, Proc. Phys. Soc. B63 (1950) 737.
  10. R.K.Luneberg, Mathematical theory of optics, CaliforniaUniversity Press, (1964), 353.
  11. V.P. Nayyar, B.L. Mehta, and M.C. Dubey, J. Phys. D. Apply. Phys. 5 (1972) 64.