Keywords
|
| Genetic Algorithm (GA), Load Transfer Capability, Available Transfer Capability, Optimal Power Flow, Contingency. |
INTRODUCTION
|
| `Optimization is performed to minimize generator –operating cost with set of constraints that represent a model of the transmission system within which the generators operate. Available transfer capability (ATC) based congestion management commission (FERC) established a system where each ISO would be responsible for monitoring its own regional transmission system and calculating the Available transfer capability (ATC) for potentially congested transmission paths entering , leaving and inside its network. ATC is a measure of how much additional electric power can be transferred from starting point to end point of a depth. [1] In this paper, optimal power flow based on available transfer capability (ATC) has been proposed for contingent power systems. In general, the total production cost is commonly used as the main objective for optimal power flow problems. However, in some circumstances, where the economical point of views is less important such as under an emergency state of partial blackout, the transmission security objective e.g. ATC is very useful. Maximizing the ATC implies to reduce probability of wide area blackout as a consequence. This paper performs contingency analysis of the power system. After an occurrence of some specific component failure, an ATC based optimal power flow problem has been formulated and solved by differential evolution (DE) method. [2]In this study the change of Available Transfer Capability for Power System including largescale wind farms. At present, the induction wind turbines have become the dominating type. The working principle of induction wind turbine, and used PQ model to analyse wind power. According to the relation between load distribution and power flow feasible boundary, a optimization model of power system based on Interior-Point Method is established to calculate Available Transfer Capability of the system. Comparing the trends of ATC and the wind power into the system . [3] This paper presents an optimal power flow (OPF) model which maximizes system security. Loading factor has been chosen as objective function of OPF problem to enhance system security. It is demonstrated that available transfer capability (ATC) is a suitable criterion for evaluation of system security. On the other hand, loading factor (LF) is an alternative concept that can evaluate system ATC.[4] A problem based on transient thermal circuit equation and modified thermal limits was involved in mathematic model of optimal power flow(OPF) about available transfer capability (ATC). The weakest lines were found applying modal analysis, the transmitting capacity was conditioned by the temperature variation of the lines by using constraints of temperature substitute for the thermal limits of the weakest lines. The solution of the optimal power flow problem by a nonlinear primal-dual interior point method is considered. [5] This paper deals with the development of an interior point nonlinear programming methodology for evaluating dynamic ATC. By establishing a novel method for integrating transient stability constraints into conventional steadystate ATC problem, the dynamic ATC solution methodology using a transient stability constrained OPF (TSCOPF). [6] In this paper, attention is particularly focused on the static synchronous series compensator and a method is proposed to determine the device best location that maximizes the power system available transfer capability measured as the maximum system load increase before any operating limit is reached. [7] In this a new decoupled approach to solve optimal power flow (OPF) and available transfer capability (ATC) problems.KKT system of original optimization problem is reformulated equivalently to no smooth equations using a so-called nonlinear complementarily problem (NCP) function. The combination of semi smooth Newton method and decoupled strategy shares those advantages of two methods such as fast convergence and saving computation cost. [8] In this paper an improved method for the calculation of available transfers capability (ATC) in a restructured power system. The ATC calculation is performed through an optimal power flow approach. The objective function is to maximize the sum of the receiving-end load in a specified area as well as to send generation to other control areas while a minimum cost of generation is continuously achieved. The constraints are AC power flow equations and system operation limits. It is assumed that the generation cost curve of each generator is available. A genetic algorithm is used for the optimization process.[9-11] discussed the study of genetic algorithm for optimal power flow solution and the parametric studies for selection of control and states variables. [12]-[13] The paper presents the calculation of Total transfer Capacity (TTC) through an optimal power flow approach. The objective function is to maximize the sum of the sending end-end generation and receivingend load of specified buses. The constraints are ac power flow equations and system operation limits. The sequential quadratic programming (SQP) method is used for the optimization process. After introduction, this paper is organized as follows – Section II gives information about Load Transfer Capability Using Genetic Algorithm. In section III problem formulation (Mathematical model) is explained, in Section IV result of case study is discussed and Section V summarizes the conclusion |
LOAD TRANSFER CAPABILITY USING GENETIC ALGORITHM
|
| The ATC problem is the determination of the largest additional amount of power above some base case value that can be transferred in a prescribed manner between two sets of buses: the source, in which power injections are increased, and the sink, in which power injections are decreased by an offsetting amount. Increasing the transfer power increases the loading in the network, and at some point causes an operational or physical limit to be reached that prevents further increase. The effects of contingencies are taken into account in the determination. The largest value of transfer power that causes no limit violations, with or without a contingency, is used to compute the ATC.The ATC problem is formulated in terms of a single unknown, the scalar parameter λ, whose value is to be maximized for each ATC case. For each transfer case, ATC is determined so as to be secure with respect to a list of contingencies. Each contingency case is processed by GA based proposed algorithms to find the maximum transfer power without causing a limit violation .The load flow solution using optimal power flow algorithm is gaining the importance in open market for operating the electrical network in optimal way. The optimal power flow is a power flow problem in which certain controllable variables are adjusted to minimize the objective function while satisfying the constraints on the physical state variables and operating limits. Many attempts were made through various algorithmic steps to obtain the global solution quickly using conventional and evolutionary methods. Evolutionary methods like Genetic Algorithm with its own advantages finds its own utility in optimal power flow solutions. Genetic Algorithm is simple to implement but has global convergence difficulties with slow convergence rate for optimal power flow problems. This paper presents three algorithm with an effect of selection of control variables on the convergence of OPF. Different sets of control variables are used to detect their usefulness in the OPF solutions. Statistical parameter based study is also provided to visualize the effect of selection of control variables on OPF convergence with solution time and improved value. Extensive study is provided on IEEE 30 bus system to draw certain important conclusions. |
PROBLEM FORMULATION: MATHEMATICAL MODELING
|
| This paper focuses on the calculation of available load transfer capability (λ) of the power system. This paper indentifies the load transfer capability as a objective function and solves the multi constraints non-linear problem with the help of genetic algorithms. three objective function viz. Power system load transfer capability , power loss in transmission line and voltage deviation. |
| 3.1 Load Transfer Capability of the System |
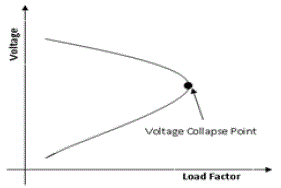
| Available Load Transfer Capability λ is the value of maximum load transfer at the critical point or within the operating system security limits or before it undergoes voltage collapse . The P – V curve is shown in fig.1 |
| The loads on power system increases gradually from initial point to the voltage collapse point i.e. up to MLP. At every load level system state is calculated until the maximum or critical condition is reached. In order to assess and enhance voltage security conditions, λ is then evaluated using Dynamic Programming. The P- V curve is shown in figure 3. |
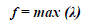 (1) (1) |
| Where λ is the maximum load transfer capability factor. |
| 3.2 Transmission Line Loss |
| The aim is to minimize total active power loss |
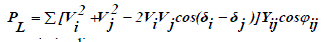 (2) (2) |
| in transmission line. |
| Where VI and δi are the magnitude and angle of voltage at bus i, respectively and Yij and φij are the magnitude and angle of the admittance of the line between bus i to bus j. |
| 3.3 Voltage Deviation |
| To have an improved voltage regulation (profile), the voltage deviation at each load bus must be made as small as possible. The voltage deviation to be minimized is as follows: |
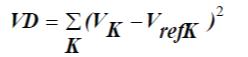 (3) (3) |
| Where Vk is the voltage magnitude at load bus k and Vref k is the nominal or reference voltage at bus k. |
| All the three objective functions are subject to the following constraints – |
| Active power balance in the network |
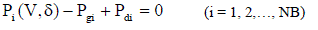 (4) (4) |
| 1. Reactive power balance in the network |
 |
| 2. Security related constraints called as soft constraints |
| a. Limits on real power generation. |
 (5) (5) |
| b. Limits on voltage magnitude |
 (6) (6) |
| c. Limits voltage angles |
 (7) (7) |
| 3. Functional constrain which is a function of control variable |
| a. Limits on reactive power |
 (8) (8) |
| Line flow limits |
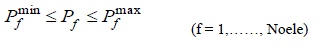 (9) (9) |
| The active power and reactive power flow on lines can be applied as follows, |
| The real power flow equation is |
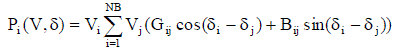 (10) (10) |
| The reactive power flow equation is |
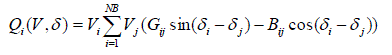 (11) (11) |
| Where, |
| NG is number of generator buses |
| NB is number of buses |
| Noele is number of transmission lines |
| NV is the number of voltage control buses |
| Pi is the active power injection into bus i |
| Qi is the reactive power injection into i |
| Pdi is the active load (demand) on bus i |
| Qdi is the reactive load (demand) on bus i |
| Pgi is the active generation on bus i |
| Qgi is the reactive generation on bus i |
| Vi is the magnitude of voltage at bus i |
| i ? is the voltage phase angle at bus i |
| Yij = Gij+jBij are the elements of admittance matrix |
RESULTS & DISCUSSION
|
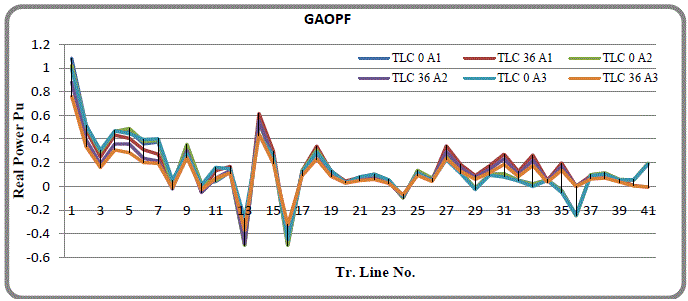
| Real Power allocation in Algorithm 1,2 & 3 are shown in Fig.2 for Cross over(CV)0.1 & Mutation (μ) 0.1 with NO Line (0) Contingency & with Line no.36 contingency .The Real Power flow in the line are required less in case of Algorithm 3, as compared to other Algorithms. |
| TLC 0-No line(0) contingency ,TLC 36 –Line no. 36 contingency condition. (A1,A2,A3) Algorithm 1,2&3. |
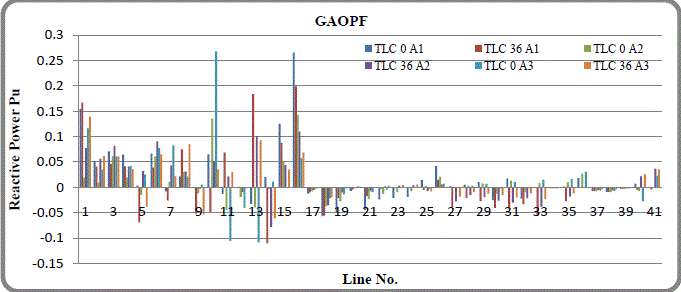
| While Fig.3 shows the Reactive Power Flow in both No Line (0) Contingency condition & with Line no.36 Contingency condition. In Algo3, the reactive power flow in the line no. 15, 24, 27 & 32 is almost zero, for no contingency condition. Under line no.36 contingency condition, the line no. 20, 21,& 26 the reactive power flow is zero. Similarly in Algo.1, the reactive power flow in the line no.12, 23 & 24 is almost zero, in contingent condition. |
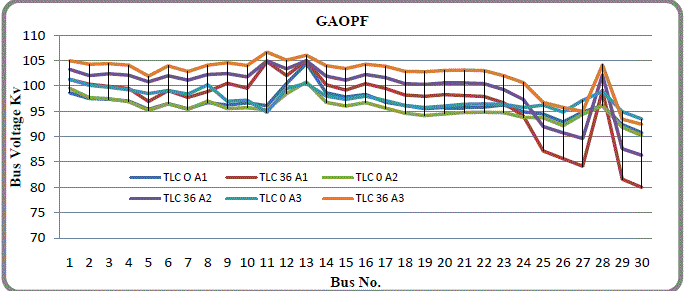
| Bus Voltage profile is shown in fig.4 , with respect to this voltage profile , it is seen that the bus voltages in the Algo.3 under line no.36 contingent condition are on higher sides as compared to the voltages in the Algo 1& 2. In Algo 1, four time i.e. the bus no.25, 26, 27 & 29, the bus voltages are below the lower set limit . In Algo 2, three times, i.e. bus no.27, 29 & 30, the bus voltages are below the set limits. Voltage limit is 10% (upper & lower limit). |
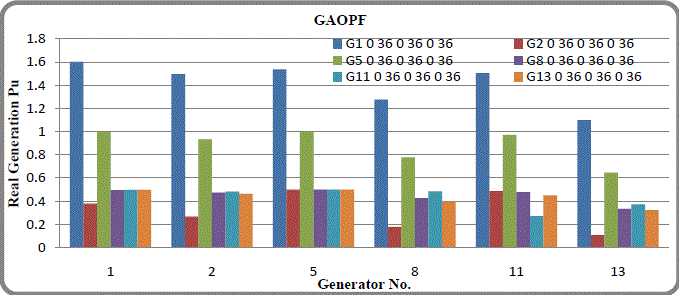
| Fig.5 shows that the Real Power Generation for no contingency & with contingency condition. Generator no. 1 ,will supplied the Real power to its maximum capacity in both 0 & 36 line contingency condition as compared other generators. The Real Power generation is approximately same in all generators. |
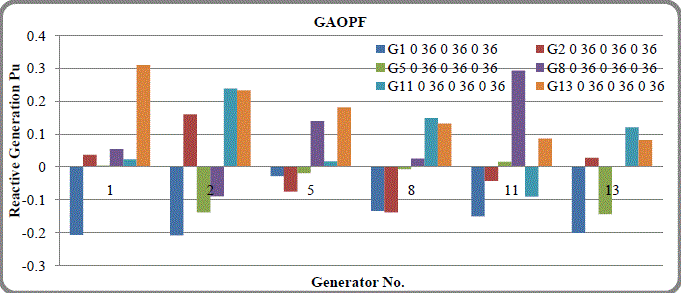
| Fig. 6 shows the Reactive Power allocation is maximum in the generator no.11 & 13. |
| From the above Table it is observed that, in Algorithm 1, 61% lines are transferring the load less than its capability .In Algorithm 2, the 63.4% lines are transferring more load than its capability. In Algorithm 3, the 75.6% lines transfers more load than there rated capability. It is also observed that, in Algorithm 3, 41.46% lines are capable of transferring load double than there capability. This shows that the Algorithm-3, the load transfer capability is more than Algorithm1 & Algorithm2. |
CONCLUSION
|
| In this study, the three Genetic Algorithms were presented. In Genetic Algorithm1, the Available Load Transfer Capability is less as compared to Genetic Algorithm 2& 3 . Genetic Algorithm 3 improved the load transfer capability in better way than the other Genetic Algorithms, within the system limit or with maintaining the system in secured condition. |
Tables at a glance
|
 |
| Table 1 |
|
| |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
 |
 |
 |
| Figure 4 |
Figure 5 |
Figure 6 |
|
| |
References
|
- Cholsuk, C. ; Inst. of Eng., Suranaree Univ. of Technol., NakhonRatchasima, Thailand ; Pao-La-Or, P. ; Kulworawanichpong, T. “ATC basedoptimal power flow for contingent power systems using differential evolution” Electrical Engineering/Electronics, Computer, Telecommunicationsand Information Technology (ECTI-CON), 2013 10th International Conference on,15-17 May 2013, 1 – 4.
- Lu Jinling ; Schooling of Electr. & Electron. Eng., North China Electr. Power Univ., Baoding, China ; Wei Zengzhen ; Tian Ying “Research onavailable transfer capability for power system including large-scale wind farms”, Electrical and Control Engineering (ICECE), 2011 InternationalConference on,16-18 Sept. 2011 , 2484 – 2487.
- Kenari, M.T. ;Electr. Eng. Dept., Iran Univ. of Sci. & Technol., IUST, Tehran, Iran ; Jadid, S.“Optimal power flow considering system security using loading factor” Environment and Electrical Engineering (EEEIC), 2010 9th InternationalConference on ,16-19 May 2010 , 234 – 237.
- GuoqingLi ;Yinfeng Sun ; Xiaojun Li “Available transfer capability calculation considering amended thermal limits” Sustainable PowerGeneration and Supply, 2009. SUPERGEN '09. International Conference on, 6-7 April 2009,1 – 7.
- Kubokawa, J. ; Hiroshima Inst. of Technol., Hiroshima ; Yue Yuan ; Yorino, N. ; Zoka, Y. “A Solution of Total Transfer Capability UsingTransient Stability Constrained Optimal Power Flow” Power Tech, 2007 IEEE Lausanne, 1-5 July 2007, 2018 – 2022.
- Menniti, D. ; Dept. of Electron., Comput. & Syst. Sci., Calabria Univ. ;Scordino, N. ; Sorrentino, N.“A new method for SSSC optimal location to improve power system Available Transfer Capability” Power Systems Conference and Exposition,2006. PSCE '06. 2006 IEEE PES, Oct. 29 2006-Nov. 1 2006 ,938 – 945.
- Xiaojiao Tong ; Inst. of Mathematics, Changsha Univ. of Sci. & Technol. ; Yongping Zhang ; Wu, F.F “ A decoupled semismooth Newtonmethod for optimal power flow” Power Engineering Society General Meeting, 2006. IEEE, 10.1109/PES.2006.11709065.
- Mozafari, B. ; Niroo Res. Inst., Sharif Univ. of Technol., Tehran, Iran ; Ranjbar, A.M. ; Shirani, A.R. ; Barkeseh, A.” A comprehensive methodfor available transfer capability calculation in a deregulated power”, Electric Utility Deregulation, Restructuring and Power Technologies, 2004.(DRPT 2004). Proceedings of the 2004 IEEE International Conference on 5-8 April 2004, Vol.2, 680 – 685.
- C.M.Wankhade, A.P.Vaidya,”Comparative Study of GA Based Optimal Power Flow”, International Journal on Advance Electrical andElectronics Engineering, on 28 June 12,Vol.1,Issue-1,20-25.
- C.M.Wankhade,B.P.Saoji,A.P.Vaidya,”Optimal Power Flow Evaluation of Power System using Genetic Algorithm “International Journal ofPower System Operation and Energy Management, Dec 2012 ,Vol.1,Issue-4, 67-72.
- C.M.Wankhade, A.P.Vaidya,”Optimal Power Flow using Genetic Algorithm: Parametric Studies for selection of Control & States Variables”,British Journal of Applied Science & Technology, published on Feb 2014, Vol.4, Issue-2,279-301.
- Shaaban, M. ; Dept. of Electr. & Electron. Eng., Hong Kong Univ., Hong Kong ; Yixin Ni ; Wu, F.F. “Transfer capability computations inderegulated power systems” System Sciences, 2000. Proceedings of the 33rd Annual Hawaii International Conference on,4-7 Jan. 2000
- B.P.saoji, A.P.Vaidya, “Hypothetical Study For Selection Of Optimal Location Of Multiple FACTS Devices Under Contingent Condition UsingDifferent Objective Functions” Electrical and Electronics Engineering: An International Journal (ELELIJ) Vol 2, No 4, November 2013”
|