INTRODUCTION
|
| A current line of research involving EEG data is the development of Brain-Computer Interfaces (BCIs). BCI can be defined as “no language and no behaviour communication” between the human brain and machine. At present, many approaches to realize the interaction between braiaxe3n and computer have been put forward, such as using Visual-Evoked Potentials (VEP), Event- Related Potentials (ERP) or EEG of different mental tasks. Comparing with other BCI methods [3], the method based on mental EEG signals has some advantages, for example, its realization need not the outside stimulation and body behaviour. In addition, early studies have showed when a person performs different mental tasks, the EEG signals take different shapes (rhythms) and the energy distribution varies between left and right hemisphere. These phenomena make it possible to detect the different mental tasks based on mental EEG signals. The features of the mental EEG signals, which are measured during different mental tasks, can extract and analyze them with different methods, and then these signals can classified into different mental state. This will contribute to the study of brain cognitive science and BCI research. The result can help to recognize the mental process and to understand the physiological mechanism of thinking. When the EEG signals measured by electrodes placed on the scalp and are always under the influences of artifacts. |
BRAIN WAVES AND ARTIFACTS IN EEG
|
| As revealed by spectral analysis, the EEG consists of mixtures of multiple frequency components, although the range of clinical interest is approximately between 0.3 and 40 Hz. Scalp EEG signals are synchronous discharges from cerebral neurons detected by electrodes attached to the scalp. Four major frequency ranges (waves) are identified in EEG that are called delta, theta alpha, and beta. Delta is the frequency range up to 4 Hz, it is preponderant in deep sleep stages of normal adults, and is often associated with very young age or certain kinds of encephalopathies. Theta is the frequency range from 4 Hz to 8 Hz and is associated with drowsiness, childhood and adolescence, as well as during drowsiness and sleep in adults. Presence of high theta activity in awake adults suggests abnormal and pathological conditions. Alpha (Berger’s wave) is the frequency range from 8 Hz to 12 Hz. It is characteristic of a relaxed, alert state of consciousness. Alpha rhythms are best detected with the eyes closed. Alpha attenuates with drowsiness and open eyes, as well as other mental efforts like thinking. They typically appear over the occipital (visual) cortex. Beta is the frequency range above 12 Hz, mostly marked in fronto-central region with reduced amplitude with respect to alpha rhythms. Low amplitude beta with multiple and varying frequencies is often associated with active, busy or anxious thinking and active concentration. Rhythmic with various pathologies and drug effects. Artifacts are generally nonlinear and nonstationary dynamic changes interfering with EEG recordings normally segregated to appropriate sub-bands of frequency. They can be subdivided in two categories: internal (biological) and external ones. The former have biological but noncognitive origin, like, for example, EOG and EMG. The latter have external origin, generally linked to the electrical line noise, to the impedance or settling of the electrodes. Among the internal artifacts, there are the eyeball artifacts, that are caused by the electric potential difference between the cornea and retina, which is quite large compared to the potentials of cerebral origin. Some small or large reflexive eye movements occur very frequently and generate a potential which can be recorded in the fronto-polar and frontal leads in the frequency range of 1-3 Hz (within the delta waves range). Vertical or horizontal movements (saccades) are caused by ocular muscles and they also generate EMG potentials. Every movement of the patient generates EMG potentials that can be picked up everywhere on the scalp; the spectrum of such signals is concentrated in the frequencies above 20Hz (within the beta range). External artifacts originate from outside the patient. Movements by the patient, or even just settling of the electrodes, may cause discontinuities and spikes originating from a |
| sudden and transient change in the impedance of a given electrode. Moreover, grounding of the EEG electrodes can cause a significant electrical line noise at 50/60 Hz; however, this artifact is easily removable by a notch filter. |
LIMITATIONS WITH THE CLASSICAL METHODS
|
| Classical methods for removing eyeblink artifacts can be classified into rejection methods and subtraction methods. |
| Rejection Methods consist of discarding contaminated EEG, based on either automatic or visual detection. Their success crucially depends on the quality of the detection, and its use depends also on the specific application for which it is used. Thus, although for epileptic applications, it can lead to an unacceptable loss of data, for others, like a Brain Computer interface, its use can be adequate. |
| Subtraction Methods are based on the assumption that the measured EEG is a linear combination of an original EEG and a signal caused by eye movement, called EOG. The EOG is a potential produced by movement of the eye or eyelid. The original EEG is hence recovered by subtracting separately recorded EOG from the measured EEG, using appropriate weights (rejecting the influence of the EOG on particular EEG channels). |
| More recently, new method ICA, based on the concept of BSS, have been proposed in order to separate neural activity from muscle and blink artifacts in spontaneous EEG data. ICA presents some advantages compared to other rejection methods. |
ICA ALGORITHMS AND THEIR METHODOLOGY
|
| Among various BSS methods the ICA extensively used for biomedical signal processing, as it separates the components in terms of their statistical independence. ICA is an extension of PCA but it is more powerful that PCA in the field of signal analysis. In mid 90’s several new ICA algorithms were introduced with impressive demonstrations on problems like separating different speech signals from a mixed signal. The applications of ICA include but not limited to the fields of biomedical, telecommunications, audio and video signal processing, feature extraction, data mining, and functional time series analysis. Generally, ICA technique can be regarded as a technique to separate signals from a mixture. These signals can be mixed linearly or nonlinearly but most of the time it is assumed that signals are mixed linearly and that’s what it is assumed in this |
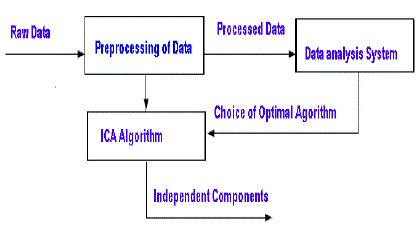
| There are several ICA algorithms in use. Some of these algorithms are FastICA, JADE and First Order Blind Identification (FOBI), Maximum Likelihood and Infomax, algorithms based on Kernel methods, and algorithms using time structure like Second Order Blind Identification (SOBI) etc., If the independent components have non-gaussian distribution then all of these and other algorithms not mentioned here work. If data is also time dependent then even if the independent components have Gaussian distribution, time-structured algorithms like SOBI can be used to find independent components. Hence as far as convergence is concerned most of the algorithms do converge as long as independent components have nongaussian distribution, at least theoretically. However practical observations are somewhat different, it is possible that some algorithms converge for one type of data while others do not. Convergence of different algorithms have already been explored and it has already been established that some algorithms converge better and faster than the others, but it is quite possible that the faster converging algorithms do not converge for some specific type of data at all while some other algorithm does or some algorithms give better estimate of the mixing matrix while others do not. Fig.1 shows how frame work for selecting the ICA algorithm. A.ICA model |
| model is as follows: Consider a simple linear model which consists of N sources of T samples i.e.., Si [s(1)i ....s(t)i ....si (T )] . The symbol t here represents time but it may represent some other parameter like space. M weighted mixtures of the sources are observed as X, where X [x (1)....x (t).....x (T)] i i i i . This can be represented as in Eqn.(1) |
 |
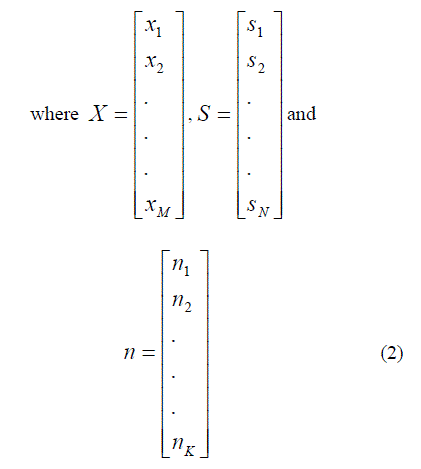 |
| and n represents the Additive White Gaussian Noise (AWGN). It is assumed that there are at least as many observations as sources i.e., M N . The M N matrix A is represented as in Eqn.(3) |
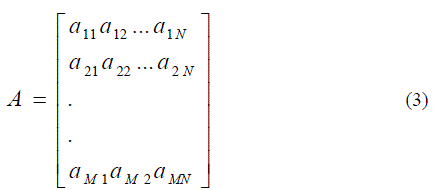 |
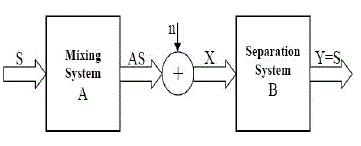
| Relates X and S. A is called the mixing matrix. The estimation of the matrix S with knowledge of X is the linear source separation problem. This is schematically shown in Fig.2. A is the mixing matrix and B is the unmixing matrix. |
| The source separation problem cannot be solved if there is no knowledge of either A or S apart from the observed mixed data X. If the mixing matrix A is known and the additive noise n is negligible then the original sources can be estimated by evaluating the pseudo inverse of the matrix A which is known as the unmixing matrix B as shown in Eqn.(4) |
 |
| For cases where the number of observations M equals number of sources N (i.e. M =N), the mixing matrix A is a square matrix with full rank and B = A-1. |
| The necessary and sufficient condition for the pseudo-inverse of A to exist is that it should be of full rank. When there are more observations than the sources (i.e. M >N), there exist many matrices B which satisfy the condition BA = I. Here the choice B depends on the components of S that we are interested in. When the number of observations is less than the number of sources (i.e. M <N), a solution does not exist unless further assumptions are made. |
| On the other side of the problem, if there is no prior knowledge of the mixing matrix A then the estimation of both A and S is known as the BSS problem. The problem defined in Eqn.(1) under the assumption of negligible Gaussian noise n is solvable with the following restrictions. |
| The sources (i.e. the components of S) are statistically independent. At most one of the sources is Gaussian distributed The mixing matrix is of full rank.Above discussion leads to following definition of ICA: Definition: ICA is a linear transformation S=WX of a multivariate signal X, such that the components S of are as independent as possible in the sense of maximizing some objective function ( , ,..... ) 1 2 N f S S S , which is a measure of statistical independence. |
| 1.Fast ICA Algorithm |
| The fast and robust fixed point ICA called Fast ICA algorithm is proposed by Hyvarinen, which is a fixedpoint algorithm based on an optimization of negative entropy function. Fast ICA is perhaps the most efficient ICA algorithm in the sense that it is very fast and there are no adjustable parameters. This algorithm is based on the very basic assumption of ICA that the mixed independent variables can not have Gaussian distribution. |
| 2.JADE Algorithm |
| JADE is developed by Cardoso and Souloumiac and is based on higher-order cumulant tensors, more specifically fourth order cumulate tensor of the input data vector. Tensors can be considered as generalization of matrices or linear operators. Cumulant tensors are then generalization of covariance matrix if data has zero mean. |
| 3.Infomax Algorithm |
| Sejnowski. The Infomax method uses a gradient-based algorithm which leads to low complexity in terms of implementation.The basic idea of the Infomax principle is to match the slope of the nonlinear transfer function of the elementary processing unit (e.g., neuron) in a network with the input Probability Density Function (PDF). The blind source Infomax nonlinear information maximization algorithm performs on-line stochastic gradient ascent in the Mutual Information (MI) between outputs and inputs of a neural-like network. Maximizing the information transfer in a nonlinear Neural Network (NN) minimizes the MI among the outputs when optimization is done over both the synaptic weights and the nonlinear transfer function. By minimizing the MI between its outputs, the network factorizes the input into independent components. |
| 4.Extended Infomax AlgorithmThe algorithm of Bell and Sejnowski which uses a sigmoidal activation function is specifically suited to separate signals with super-Gaussian distribution (i.e. positive kurtosis). Lee and Sejnowski proposed an extension of Infomax ICA that is able to separate with sub and as well as super Gaussian distribution. This preserves the ICA architecture of Infomax algorithm, but it uses a learning rule derived by Girolami and Fyfe. It determines the sign changes (positive to negative and vice versa) required by the algorithm to handle both sub and super Gaussian distributions. |
| V. Results |
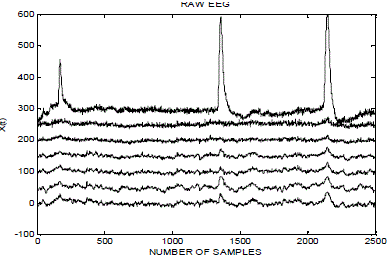
| Fig.3 shows one subject's EEG data obtained from doing maths tasks twice. From the Fig.3, we can see that the EEG recordings contain obvious eye artifacts. |
COMPARISON OF ALGORITHMS
|
| As we calculated the PSNR value and the execution time for all the four algorithms, we were taken the effective PSNR value and execution time to conclude our work where the comparision for each algorithms is tabulated in Table 1 |
CONCLUSION
|
| ICA is the central topic in this project. EEG signals will maintain the similarity in their patterns when subject is performing the mental task. The traditional methods applied for remove artifacts can only compromise between eliminating artifacts and protecting useful signals so that the result is not very satisfying. However, ICA method can protect the useful signals as well as obviously weaken even entirely remove the artifacts in multi channel EEG signals, this characteristic of ICA is the key to get stable EEG patterns which can be used for mental task classification. Simulation results of the four ICA algorithms in are presented. Results are discussed and their performance has been compared. The EEG is reconstructed without artifacts. Thus from the tabulated results it has been concluded that JADE has better performance in short time period when compared to other ICA algorithms analysed. |
Tables at a glance
|
 |
| Table 1 |
|
| |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
| |
References
|
- AapoHyvarinen,” Independent Component Analysis:Algorithmsand IEEE transactions on NeuralNetworks,vol.13,pp.411-430,2000.
- D,Bickford,“Electroencephalography”,In:AdelmamG.ed.Encyclopedia of uroscience, Brikhauser, Cambridge (USA)
- A.Cichoki and S.Vorobyov Application of ICA for automaticnoise and interference cancellation in multisensory biomedicalsignals,”In proceedings of Second International Workshop on ICAand BSS,pp.621- 626,June 2000.
- M.Laubach and M.Shuler,”A Unifying Information-theoreticFramework for Independent ComponentAnalysis,” Comp.mat.appl.vol.31,pp.1-21,April 2003.
- M.Teplan,”Fundementals of EEG measurement”
|